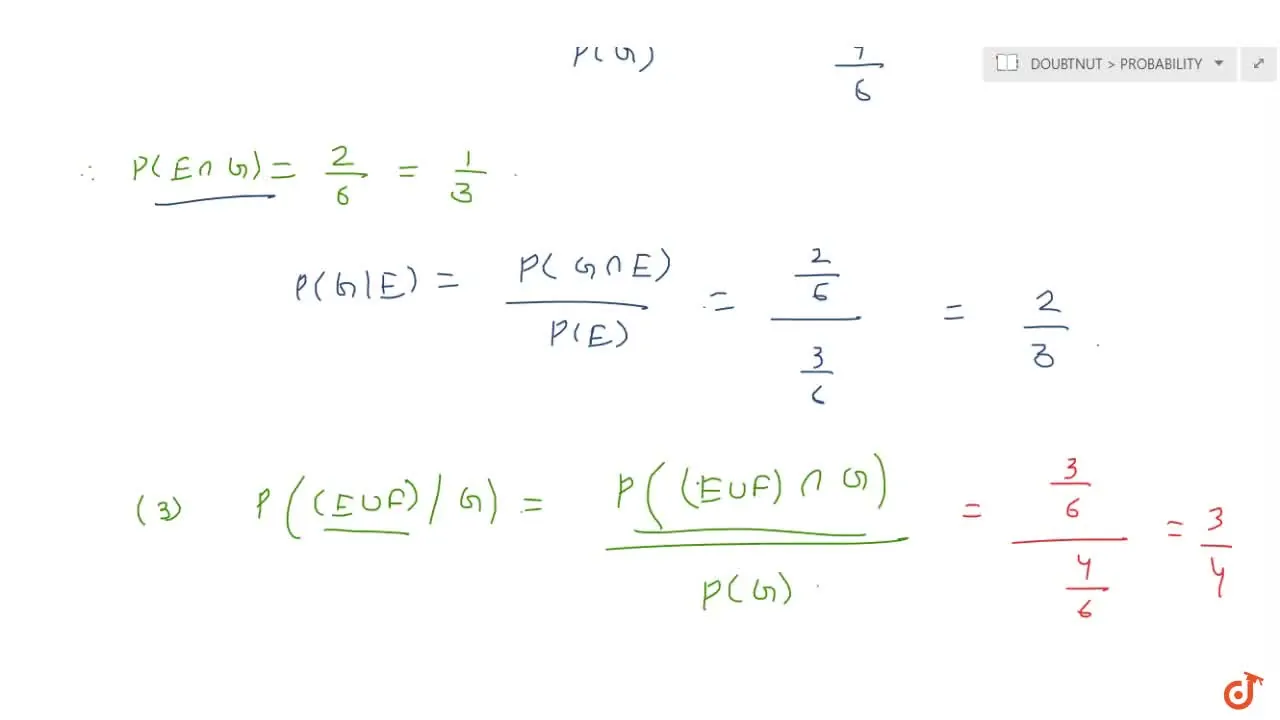A fair die is rolled. Consider events E={1,3,5}, F={2,3}and G={2,3,4,5}Find(i) P(E∣F)and P(F∣E) (ii) P(E∣G)and P(G∣E) (iii) P((E∪F)∣G)and P((E∩F)∣G)
Solution: We are given with the following information-
E={1,3,5},F={2,3},G={2,3,4,5}
.
A dice is rolled,so, we will consider following events - E={1,3,5};P(E)=36=12,F={2,3};P(F)=26=13,G={2,3,4,5};P(G)=46=23
, now,E∩F={3},so,P(E∩F)=16;
(i)P(E∣F)=P(E∩F)P(F)=1613=12
;P(F∣E)=P(F∩E)P(E)=P(E∩F)P(E)=1613=16×12=13
;(ii)P(E∣G)=P(E∩G)P(G),and,E∩G={3,5}=P(E∩G)=26=13,now,P(E∣G)=P(E∩G)P(G)=1323=12=P(G∣E)=P(G∩E)P(E)=P(E∩G)P(E)=1323=12
;(iii)P((E∪G)∣G),E∪F=A={1,2,3,5},⇒P(A)=46=23,and,(A∩G)={2,3,5},so,P(A∩G)=36
, now,P(A∣G)=P(A∩G)P(G)=P((E∪F)∣G)=3646=34,(E∩F)=B,B={3},P(B)=16,B∩G={3},so,P(B∩G)=16,andP((E∩F)∣G)=P(B∩G)P(G),now,P((E∩F)∣G)=1646=14
Related Playlists
- BOOK - NCERTCHAPTER - PROBABILITYEXERCISE - MISCELLANEOUS EXERCISE19videos
PROBABILITY
- BOOK - NCERTCHAPTER - PROBABILITYEXERCISE - EXERCISE 13.515videos
PROBABILITY
- BOOK - NCERTCHAPTER - PROBABILITYEXERCISE - Solved Examples36videos
PROBABILITY
- BOOK - NCERTCHAPTER - MATRICESEXERCISE - EXERCISE 3.312videos
MATRICES
- BOOK - NCERTCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - EXERCISE 1.314videos
RELATIONS AND FUNCTIONS
Similar Questions
A fair die is rolled. Consider the events :
E = {1, 3, 5}, F = {2, 3} and G = {2, 3, 4, 5}.
Find : (i) P(E/F) and P(F/E)
(ii) P(E/G) and P(G/E)
(iii) P(E∪F/G) and P(E∩F/G).View SolutionA fair die is rolled. Consider E={1,3,5}, F={2,3}, G={2,3,4,5}
View SolutionA fair dice is rolled. Consider the following events: A={1,2,5},B={2,3} and C={2,3,4,5} Find (i) P(AB) and P(BC) (ii) P(AC) and P(CA) (iii) P(A∪BC) and P(A∩BC) (iv) P(A∩BC)
View SolutionIf P(E)=0−8,P(F)=0.5 and P(FE)=0.4, then P(EF)=
View SolutionIf E and F are events such that P(E)=14,P(F)=12 and P(EandF)=18, find (i) P(EorF) (ii) P (not E and not F).
View SolutionGiven that E and F are events such that P(E)=0.6,P(F)=0.3 and P(E∩F)=0.2, find P(E/F) and P(F/E).
View SolutionGiven that E and F are events such that P(E)=0.8,P(F)=0.7,P(E∩F)=0.6. Find P(E∣F)
View SolutionIf E1 and E2 are independent events such that P(E1)=0.3 and P(E2)=0.4, find (i) P(E1∩E2) (ii) P(E1∪E2) (iii) P(¯¯¯¯E1∩¯¯¯¯E2) (iv) P(¯¯¯¯E1∩E2).
View SolutionLet E1 and E2 are two independent events such that P(E1)=0.3andP(E2)=0.6. Find the value of: (i) P(E1∩E2) (ii) P(E1∪E2) (iii) P(E1/E2)(iv) P(E2/E1)
View SolutionA die is rolled. E is the event that the uppermost face shows a number multiple of 3. Write n ( E ) and P( E).
View Solution