By the graphical method, find whether the following pair of equations are consistent of not. If consistent, solve them.
(i) $3 x + y + 4 = 0, 6 x - 2 y + 4 = 0$
(ii) $x - 2 y = 6, 3 x - 6 y = 0$
(iii) $x + y = 3, 3 x + 3 y = 9$

Video Solution

Text Solution

Verified by Experts

(i) Given pair of equations is
3x+y+4=0 $... (i)$
and $6 x - 2 y + 4 = 0 ... (i i)$
On comparing with $a x + b y + c = 0$ , we get
$a_{1} = 3, b_{1} = 1$
and $c_{1} = 4$ [from Eq. (i)]
$a_{2} = 6, b_{2} = - 2$
and $c_{2} = 4$ [from Eq.(ii)] $< b r > H e r e,$ (a_(1))/(a_(2))=(3)/(6)=(1)/(2) , (b_(1))/(b_(2))=(1)/(-2) $< b r > and$ (c_(1))/(c_(2))=(4)/(4)=(1)/(1) $< b r >$ :' (a_(1))/(a_(2))!=(b_(1))/(b_(2)) $< b r > S o, t h e g i v e n p a i r o f l \in e a r e q u a t i o n s a r e \int e r sec t \in g a t o \neq p \oint, ∴ t h e s e l \in e s h a v e u n i q u e s o l u t i o n . < b r > H e n c e, g i v e n p a i r o f l \in e a r e q u a t i o n s i s c o n s i s t e n t . < b r > W e h a v e, 3 x + y + 4 = 0 < b r >$ rArr " " y=-4-3x $< b r > w h e n x = 0, t h e n y = - 4 < b r > w h e n x = - 1, t h e n y = - 1 < b r > W h e n x = - 2, t h e n y = 2 < b r >$ {:(" "x,0,-1,-2),(" "y,-4,-1,2),("Points","B","C","A"):} $< b r > and 6 x - 2 y + 4 = 0 < b r >$ rArr 2y=6x+4 $< b r >$ rArr y=3x+2 $< b r > W h e n x = 0, t h e n y = 2 < b r > W h e n x = - 1, t h e n y = - 1 < b r > W h e n x = 1, t h e n y = 5 < b r >$ {:(" "x,-1,0,1),(" "y,-1,2,5),("Points","C","Q","P"):} $< b r > P l o \in g t h e p \oint B (0, - 4) and A (- 2, 2), w e \geq t t h e s t r a i g h t l \in e A B . P l o \in g t h e p \oint s Q (0, 2) and P (1, 5), w e \geq t t h e s t r a i g h t l \in e P Q . T h e l \in e s A B and P Q \int e r sec t a t C (- 1, - 1) . < b r > < i m g a \leq ocr_image l o a d \in g = lazy s r c = https://d10lpgp6xz60nq.cloudfront.net/physics_images/ARH_NCERT_EXE_MATH_X_C03_S01_030_S01.png w h = 80% mx-auto s t y \leq = background:white; > < b r > (i i) G i v e n p a i r o f e q u a t i o n s i s$ " " x-2y=6 " " ...(i) $< b r > and$ " " 3x-6y=0 " " ...(ii) $< b r > O n c o m p a r \in g w i t h a x + b y + c = 0 . w e \geq t < b r >$ a_(1)=1, b_(1)=-2 $and$ c_(1)=-6 " " $[o m E q . (i)] < b r >$ a_(2)=3, b_(2)=-6 $and$ c_(2)=0 $[from Eq. (i i)] < b r > H e r e,$ (a_(1))/(a_(2))=(1)/(3), (b_(1))/(b_(2))= (-2)/(-6)=(1)/(3) $and$ (c_(1))/(c_(2))=(-6)/(0) $< b r >$ :. " " (a_(1))/(a_(2))=(b_(1))/(b_(2))=(c_(1))/(c_(2)) $< b r > H e n c e, t h e l \in e s r e p r e s e n t e d b y t h e g i v e n e q u a t i o n s a r e p a r a l \leq l . T h e r e f or e, i t h a s n o s o l u t i o n . S o, t h e g i v e n p a i r o f l \in e s i s \in c o n s i s t e n t . < b r > (i i i) G i v e n p a i r o f e q u a t i o n i s$ " " x+y=3 " " ...(i) $< b r > and$ " " 3x+3y=9 " " ...(ii) $< b r > O n c o m p a r \in g w i t h a x + b y + c = 0 . w e \geq t < b r >$ a_(1)=1, b_(1) $and$ c_(1)=-3 " " $[o m E q . (i)] < b r >$ a_(2)=3, b_(2)=3 $and$ c_(2)=-9 " " [from Eq. (ii)]
Here, $\frac{a_{1}}{a_{2}} = \frac{1}{3}, \frac{b_{1}}{b_{2}} = \frac{1}{3}$ and $\frac{c_{1}}{c_{2}} = \frac{- 3}{- 9} = \frac{1}{3}$
$\Rightarrow \frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} = \frac{c_{1}}{c_{2}}$
So, the given pair of lines is coincident. Therefore, these lines have infinitely many solutions. Hence, the given pair of linear equations is consistent.
Now, $x + y = 3 \Rightarrow y = 3 - x$
If x=0, then y=3, If x=3, then y=0
$\begin{matrix} x & 0 & 3 y & 3 & 0 Points & A & B \end{matrix}$
and $3 x + 3 y = 9 \Rightarrow 3 y = 9 - 3 x$
$\Rightarrow y \frac{9 - 3 x}{3}$
If x=0, then y=3, if x=1, then y=2 and if x=3, then y=0
$\begin{matrix} x & 0 & 1 & 3 y & 3 & 2 & 0 Points & C & D & E \end{matrix}$

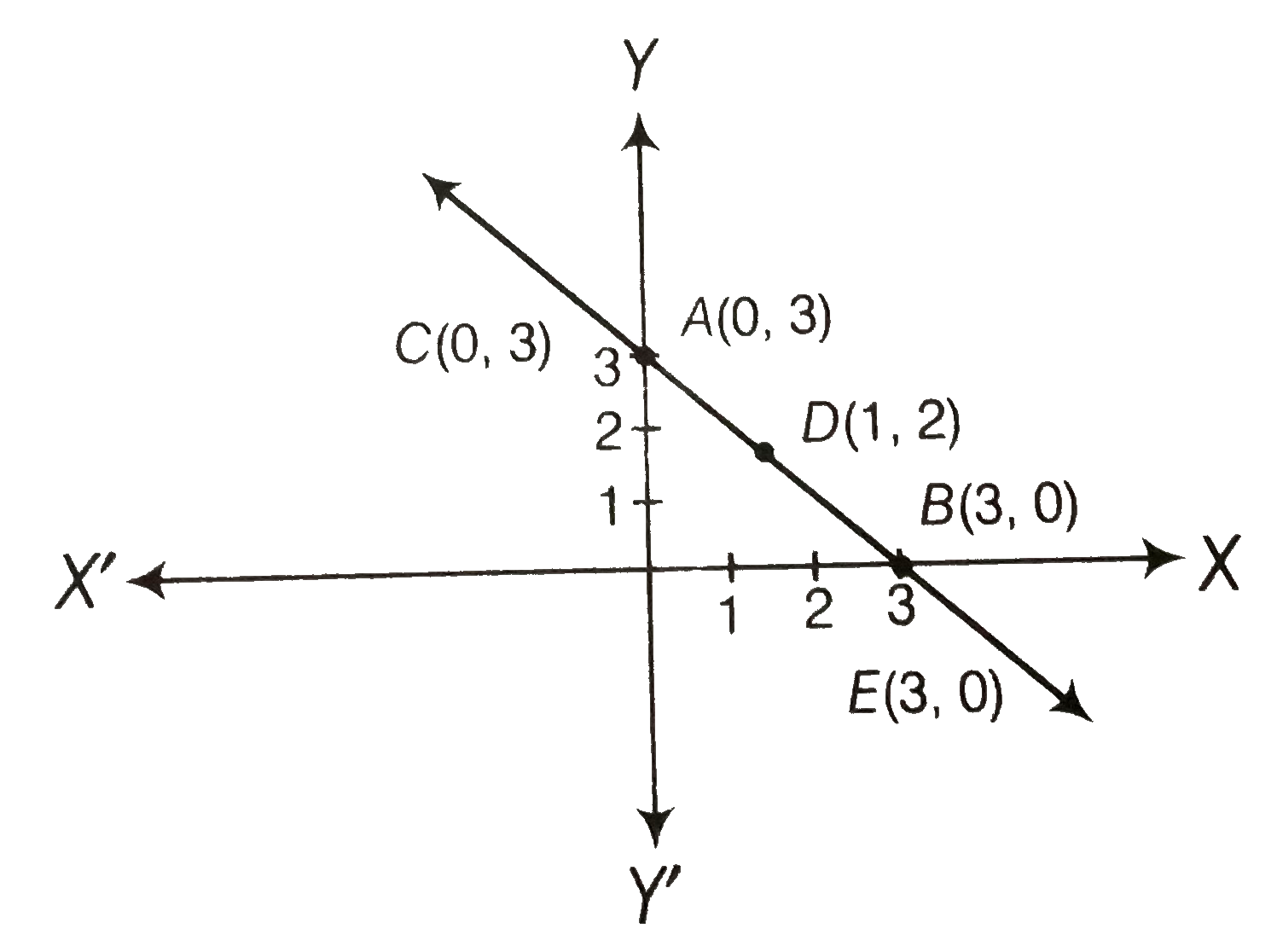
Plotting the points A (0,3) and B (3,0), we get the line AB. Again, plotting the points C(0,3)D(1,2) and E(3,0), we get the line CDE.
We observe that the lines represented by Eqa. (i) and (ii) are coincident.

Updated on:21/07/2023

|

Class 10 MATHS LINEAR EQUATIONS IN TWO VARIABLE

Topper's Solved these Questions

Similar Questions

NCERT EXEMPLAR-PAIR OF LINEAR EQUATIONS IN TWO VARIABLES-Exercise 3.3 Short Answer Type Questions

Home
Ask Doubt
Profile