The zeroes of the quadratic polynomial $x^{2} + k x + k$ where $k \neq 0$ ,

A

cannot both be positive

B

cannot both be negative

C

are always unequal

D

are always equal

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Let $p (x) = x^{2} + k x + k, k \neq 0$
On comparing $p (x)$ with $a x^{2} + b x + c$ , we get
$a = 1, b = k$ and $c = k$
Now, $x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$ [by quadratic formula]
$= \frac{- k \pm \sqrt{k^{2} - 4 k}}{2 \times 1}$
$= \frac{- k \pm \sqrt{k (k - 4)}}{2}, k \neq 0$
Here, we see that
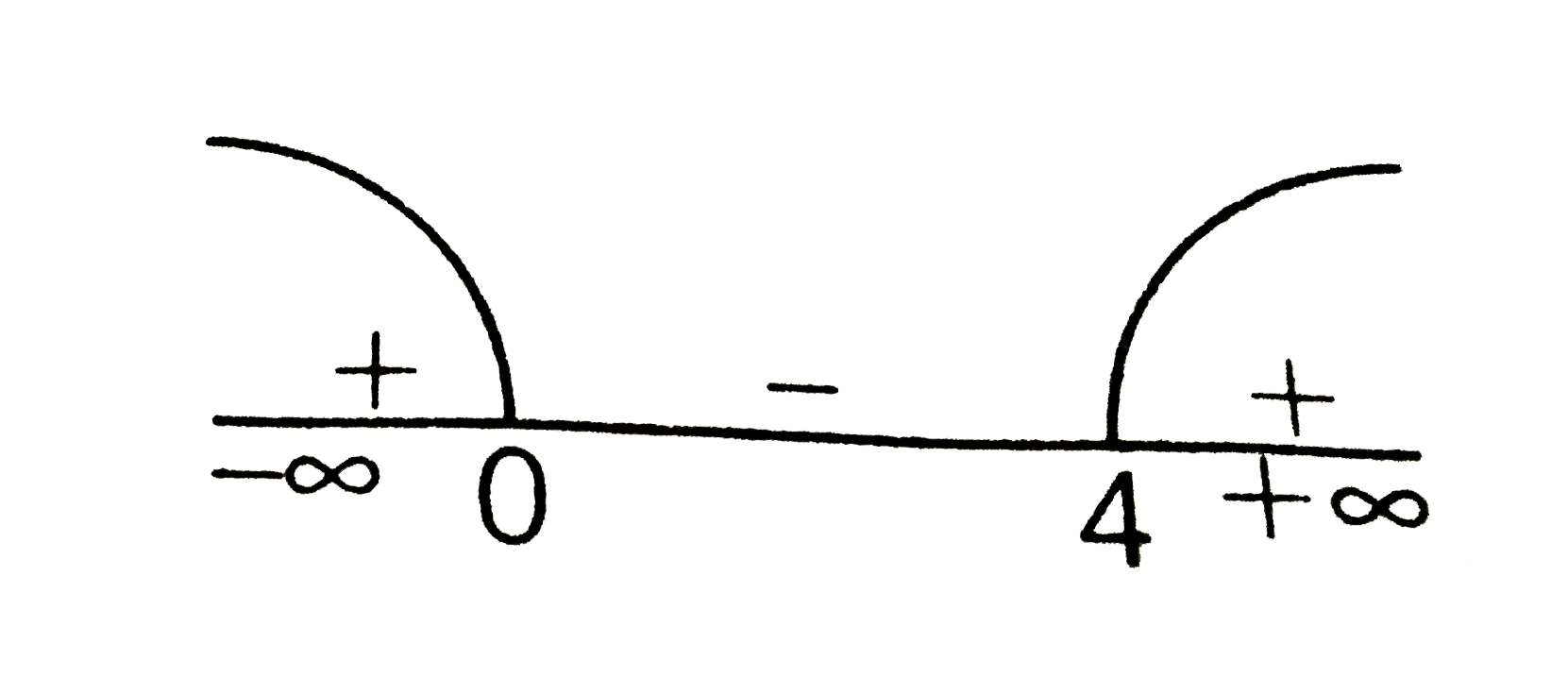
$k (k - 4) > 0$
$\Rightarrow k \in (- \infty, 0) \cup (4, \infty)$
Now, we know that
In quadratic polynomial $a x^{2} + b x + c$
If $a > 0, b > 0, c > 0$ or $a < 0, b < 0, c < 0$ ,
then the polynomial has always all negative zeroes. and is $a > 0, c < 0$ or $a < 0, c > 0$ , then the polynomial has always zeroes of opposite sign.
Case I if $k \in (- \infty, 0)$ i.e., $k < 0$
$\Rightarrow a = 1 > 0, b, c = k < 0$
So, the zeroes are of opposite sign.
Case II If $k \in (4, \infty) i . e ., k \geq 4$
$\Rightarrow a = 1 > 0, b \geq 4$
So, both zeroes are negative
Hence, in any case zeroes of the given quadratic polynomial cannot both be positive.

Updated on:21/07/2023

|

Class 10 MATHS POLYNOMIALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

The zeroes of the quadratic polynomial $x^{2} + k x + k, k \neq 0$
Acannot both be positive
Bcannot both be negative
Care always unequal
Dare always equal
If the sum of the zeros of the quadratic polynomial $k x^{2} + 2 x + 3 k$ is equal to the product of its zeros then $k = ?$
A $\frac{1}{3}$
B $\frac{- 1}{3}$
C $\frac{2}{3}$
D $\frac{- 2}{3}$
If one zero of the quadratic polynomial $k x^{2} + 3 x + k$ is 2 then the value of k is
A $\frac{5}{6}$
B $\frac{- 5}{6}$
C $\frac{6}{5}$
D $\frac{- 6}{5}$

NCERT EXEMPLAR-POLYNOMIALS -Polynomials

Home
Ask Doubt
Profile