A black body is at a temperature of 2880 K. The energy of radiation emitted by this object with wavelength between 4990 A and 5000A is E1 , and that between 9990 A and 10000 A is E2 . Find the ratio of E2 and E1.
To find the ratio of the energies E2 and E1 emitted by a black body at a temperature of 2880 K for the specified wavelengths, we will use Planck's Radiation Law.
1. Understand Planck's Radiation Law:
The energy emitted per unit wavelength by a black body is given by:
Eλ=2πhc2λ5⋅1ehcλkT−1
where:
- h = Planck's constant =6.63×10−34Js
- c = speed of light =3×108m/s
- k = Boltzmann's constant =1.38×10−23J/K
- T = temperature in Kelvin
2. Define the Wavelengths:
- For E1: Wavelength range is from 4990Å to 5000Å.
- For E2: Wavelength range is from 9990Å to 10000Å.
3. Calculate the Average Wavelengths:
- Average wavelength for E1 (λ1):
λ1=4990+50002=4995Å=4995×10−10m
- Average wavelength for E2 (λ2):
λ2=9990+100002=9995Å=9995×10−10m
4. Apply Planck's Law for Both Wavelengths:
- For E1:
E1=2πhc2λ51⋅1ehcλ1kT−1
- For E2:
E2=2πhc2λ52⋅1ehcλ2kT−1
5. Find the Ratio E2E1:
E2E1=2πhc2λ52⋅1ehcλ2kT−12πhc2λ51⋅1ehcλ1kT−1
This simplifies to:
E2E1=λ51λ52⋅ehcλ1kT−1ehcλ2kT−1
6. Substituting Values:
- Substitute λ1=4995×10−10m, λ2=9995×10−10m, and T=2880K.
- Calculate E2E1.
7. Final Calculation:
After performing the calculations, you will find:
E2E1≈4.62
The energy emitted per unit wavelength by a black body is given by:
Eλ=2πhc2λ5⋅1ehcλkT−1
where:
- h = Planck's constant =6.63×10−34Js
- c = speed of light =3×108m/s
- k = Boltzmann's constant =1.38×10−23J/K
- T = temperature in Kelvin
- For E1: Wavelength range is from 4990Å to 5000Å.
- For E2: Wavelength range is from 9990Å to 10000Å.
- Average wavelength for E1 (λ1):
λ1=4990+50002=4995Å=4995×10−10m
- Average wavelength for E2 (λ2):
λ2=9990+100002=9995Å=9995×10−10m
- For E1:
E1=2πhc2λ51⋅1ehcλ1kT−1
- For E2:
E2=2πhc2λ52⋅1ehcλ2kT−1
E2E1=2πhc2λ52⋅1ehcλ2kT−12πhc2λ51⋅1ehcλ1kT−1
This simplifies to:
E2E1=λ51λ52⋅ehcλ1kT−1ehcλ2kT−1
- Substitute λ1=4995×10−10m, λ2=9995×10−10m, and T=2880K.
- Calculate E2E1.
After performing the calculations, you will find:
E2E1≈4.62
Topper's Solved these Questions
- HEAT TRANSFER BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Discussion Question
26 Videos
- HEAT TRANSFER BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Conceptual MCQs Single Option Correct
24 Videos
- HEAT TRANSFER BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Practice Exercise 4.3
5 Videos
- HEAT AND THERMAL EXPANSIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT AND THERMAL EXPANSIONEXERCISE - UNSOLVED NUMRICAL PROBLEMS FOR PREPARATION OF NSEP, INPhO & IPhO
82 Videos
- Kinetic Theory of Gases and Gas LawsBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - Kinetic Theory of Gases and Gas LawsEXERCISE - Unsolved Numerical Problems for Preparation of NSEP, INPhO & IPhO
64 Videos
Similar Questions
A black body, which is at a high temperature TK thermal radiation emitted at the rate of E W/m2. If the temperature falls to T/4 K, the thermal radiation emitted in W/m2 will be
View SolutionA black body is at 2000 K, it emits maximum energy at a wavelength. 1μm.. The temperature, it emits at wavelength of 2μm is
View Solution
Knowledge Check
A blackbody is at a temperature of 2880K. The energy of radiation emitted by this object with wavelength between 499nm and 500nm is U1, between 999nm and 1000nm is U2 and between 1499 nm and 1500 nm is U3. The Wien constant b=2.88×106nmK. Then
AU1=0BU3=0CU1>U2DU2>U1Compare the energies of two radiations E1 with wavelength 800 nm and E2 with wavelength 400 nm.
AE1=2E2BE1=E2CE2=2E1DE2=−12E1If the rate of emission of radiation by a body at temperature TK is E then graph between log E and log T will be .
A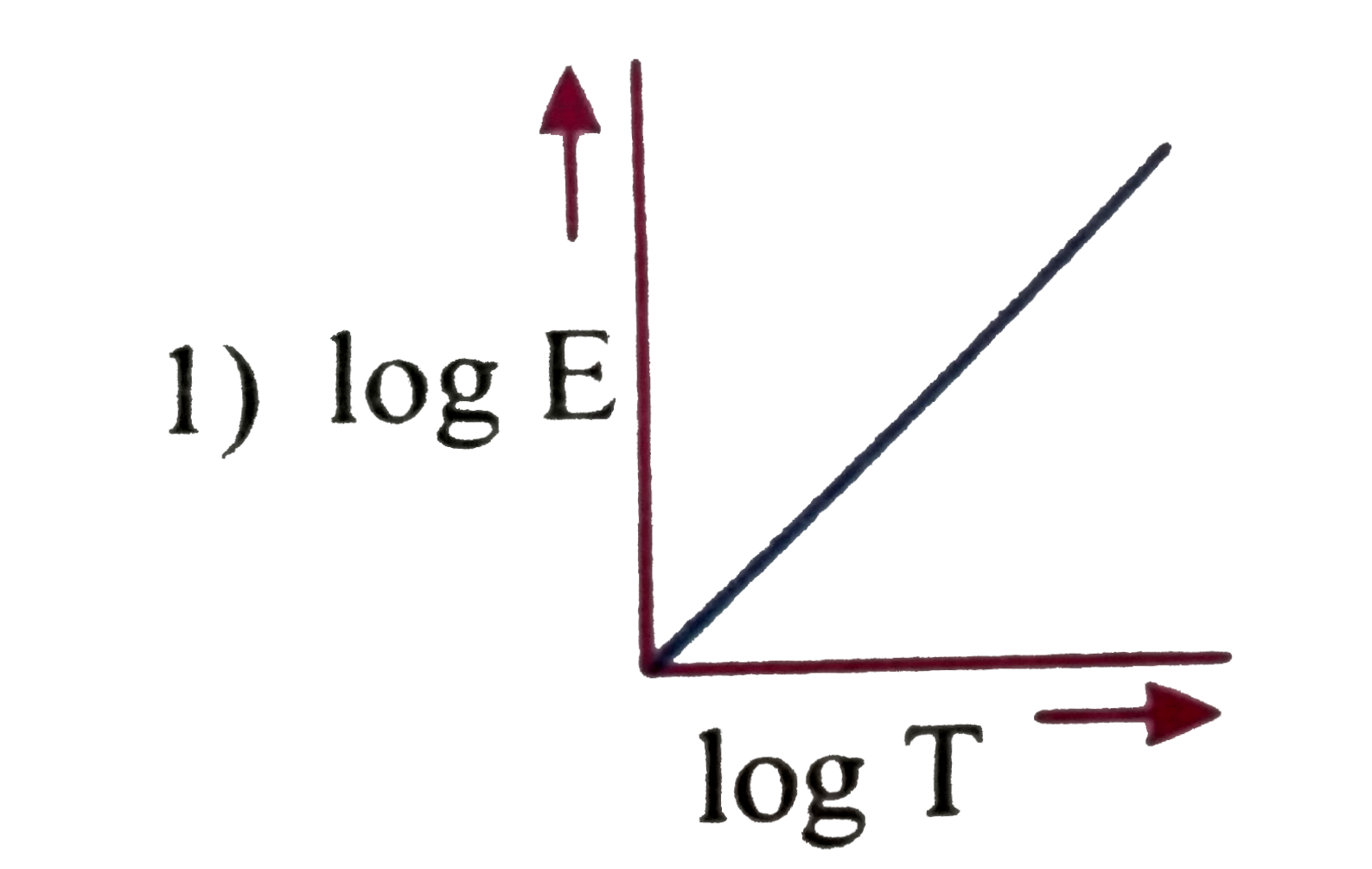 B
B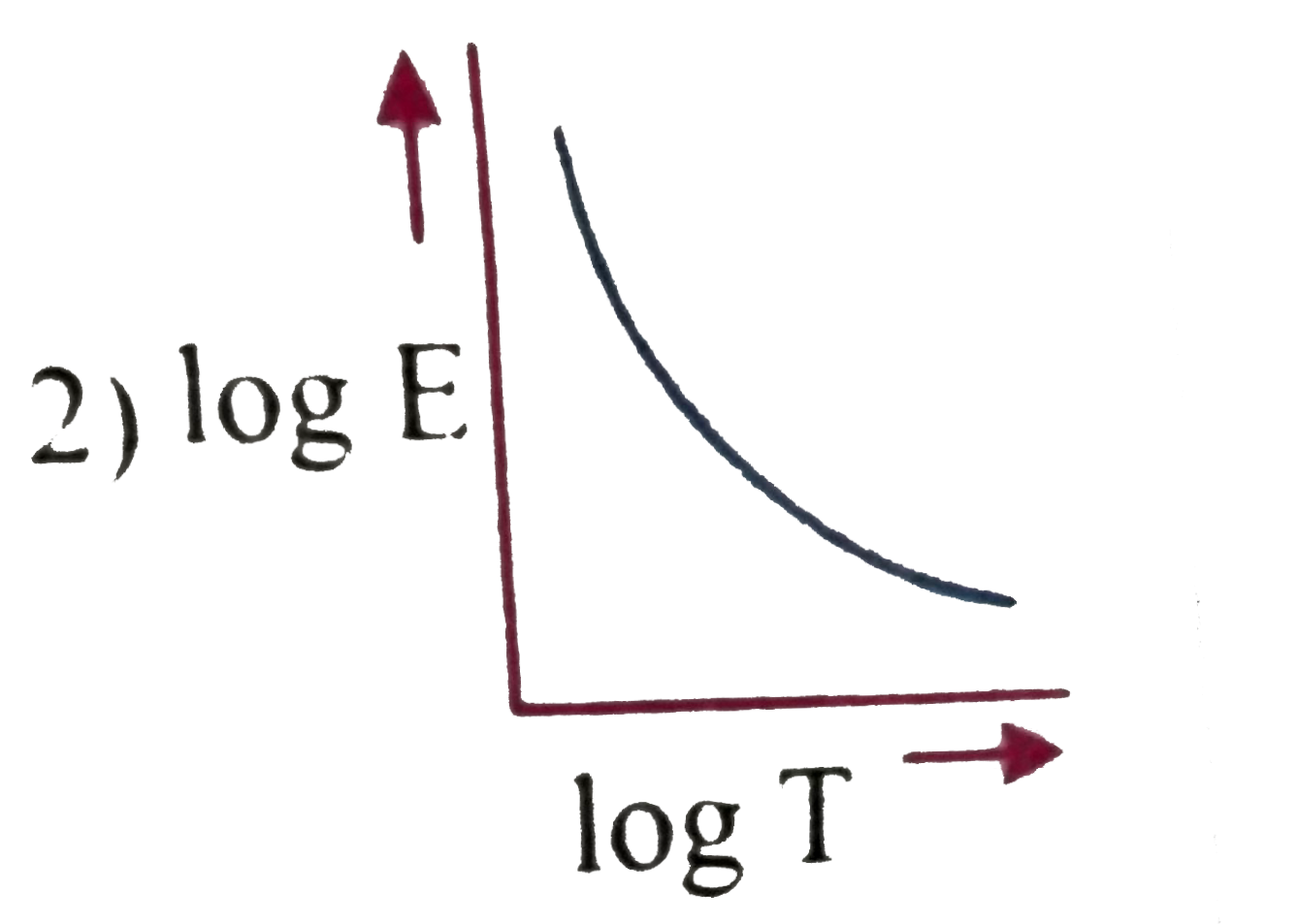 C
C D
D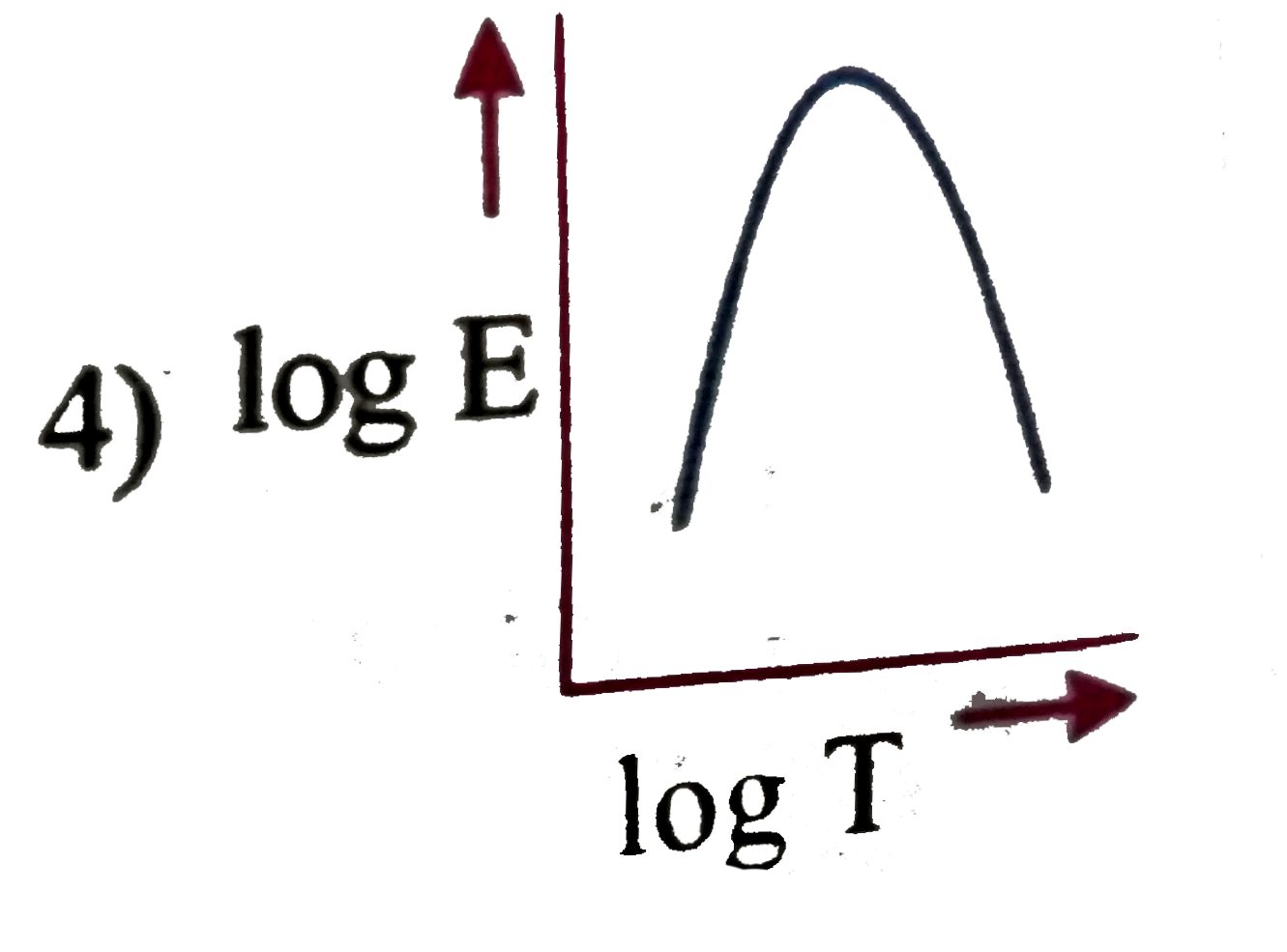
The energy of a radiation of wavelength 8000 Å is E1 and energy of a radiation of wavelength 16000 Å is E2. What is the relation between these two
View SolutionThe relationship between energy E, of the radiation with a wavelength 8000 Å and the energy of the radiation with a wavelength 16000 Å is
View SolutionAn atom emits a spectral line of wavelength λ when an electron makes a transition between levels of energy E1andE2. Which expression correctly relates λE1andE2 ?
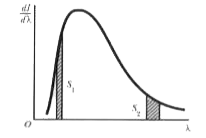
View SolutionTwo separate segments of equal area are isolated in the energy distribution of black body radiation (As shown in the following figure). Let us assume that the number of photons emitted by the body per unit time in the segments is n1andn2 and the energy of the photons are E1andE2 respectively. Then
View SolutionThe frequency of radiation absorbed or emitted when transition occurs between two stationary states with energies E1 (lower) and E2 (higher) is given by
View Solution
