A parallel plate capacitor consists of two plates of 2m×1m. The space between the plates is of 1mm and filled with a dielectric of relative permittivity of 7. A potential difference of 300 volts is applied across the plates. Find the potential gradient
6×105N/C
3×105N/C
18×105N/C
12×105N/C
The correct Answer is:B
To find the potential gradient in the parallel plate capacitor, we can follow these steps:
Step 1: Identify the given values
- Area of the plates: 2m×1m
- Separation between the plates: 1mm=1×10−3m
- Potential difference (voltage) across the plates: 300V
- Relative permittivity (dielectric constant): 7 (not directly needed for potential gradient calculation)
Step 2: Understand the formula for potential gradient
The potential gradient (also known as electric field strength, E) between the plates of a capacitor is given by the formula:
E=ΔVd
where:
- E is the potential gradient (in volts per meter, V/m),
- ΔV is the potential difference (in volts, V),
- d is the separation between the plates (in meters, m).
Step 3: Substitute the known values into the formula
Substituting the known values into the formula:
E=300V1×10−3m
Step 4: Calculate the potential gradient
Calculating the above expression:
E=3000.001=300000V/m=3×105V/m
Step 5: State the final answer
The potential gradient in the parallel plate capacitor is:
E=3×105V/mor3×105N/C
- Area of the plates: 2m×1m
- Separation between the plates: 1mm=1×10−3m
- Potential difference (voltage) across the plates: 300V
- Relative permittivity (dielectric constant): 7 (not directly needed for potential gradient calculation)
The potential gradient (also known as electric field strength, E) between the plates of a capacitor is given by the formula:
E=ΔVd
where:
- E is the potential gradient (in volts per meter, V/m),
- ΔV is the potential difference (in volts, V),
- d is the separation between the plates (in meters, m).
Substituting the known values into the formula:
E=300V1×10−3m
Calculating the above expression:
E=3000.001=300000V/m=3×105V/m
The potential gradient in the parallel plate capacitor is:
E=3×105V/mor3×105N/C
Topper's Solved these Questions
Similar Questions
The plates of a parallel plate capacitor are separated by a distance d=1cm. Two parallel sided dielectric slabs of thickness 0.7cm and 0.3cm fill the space between the plates. If the dielectric constants of the two slabs are 3 and 5 respectively and a potential difference of 440V is applied across the plates. Find (a) The electric field intensities in each of the slabs. (b) The ratio of electric energies stored in the first to that in the second dielectric slab.
View SolutionThe plates of a parallel plate capacitor are separated by 1cm .Two parallel sided dielectric slabs of thickness 0.6cm and 0.4 cm fill the space between the plates.The dielectric constants of the two slabs are 3 and 5 respectively and a potential difference of 210V is applied across the plates.Electric field in the slab of 0.6cm thick is k2×104Vm .The value of k is
View Solution
Knowledge Check
A capacitor with air as the dielectric is charged to a potential of 100 volts. If the space between the plates is now filled with a dielectric of dielectric constant 10, the potential difference between the plates will be
A1000 voltsB100 voltsC10 voltsDZeroA parallel plate capacitor has rectangular plates of 400cm2 and are separated by a distance of 2 mm with air as medium. What charge will appear on the plates. If a 200 volt potential difference is applied across the condenser
A3.54×10−6CB3.54×10−8CC3.54×10−10CD1770.8×10−13CTwo plates are 2cm apart, a potential difference of 10 volt is applied between them, the electric field between the plates is
A20N/CB500N/CC5N/CD250N/C
- The plates of a parallel plate capacitor are separated by 1cm .Two parallel sided dielectric slabs of thickness 0.6cm and 0.4cm fill the space between the plates.The dielectric constants of the two slabs are 3 and 5 respectively and a potential difference of 210V is applied across the plates.Electric field in the slab of 0.6cm thick is k−×104V/m .The value of 'k is
View SolutionA parallel-plate capacitor is filled with a dielectric up to one-half of the distance between the plates.The manner in which the potential between the plates varies is illustrated in the figure. Which half (1or2) of the space between the plates is filled with the dielectric and what will be the distribution of the potential after the dielectric is taken out of the capacitor provided that (a) the charges on the plates are conserved or (b) the potential difference across the capacitor is conserved?
View SolutionIn a parallel plate capacitor the potential difference of 100 V is manitianed between the plates. If distance between the plates be 5mm, what will be the electric field at points A and B ?
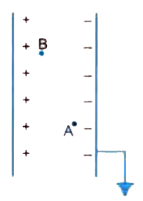
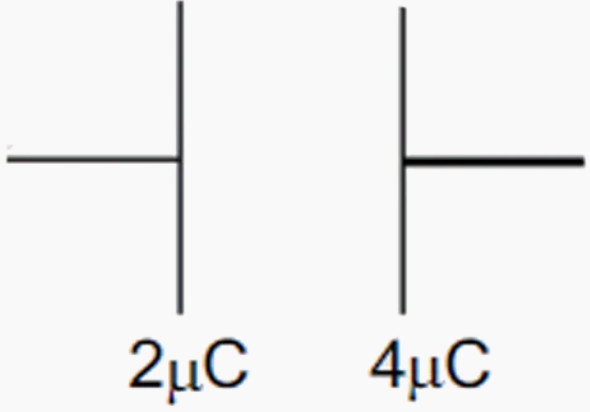
View SolutionIn a parallel plate capacitor of capacitor 1μF two plates are given charges 2μC and 4μC the potential difference between the plates of the capacitor is
View SolutionThe distance between the plates of a parallel plate condenser is 4mm and potential difference is 60 volts. If the distance between the plates is increased to 12mm, then
View Solution
