Power dissipated in pure inductance will be-
LI22
2LI2
LI24
Zero
The correct Answer is:D
To determine the power dissipated in a pure inductance, we can follow these steps:
1. Understand the Circuit: In a pure inductive AC circuit, we have an alternating current (AC) source connected to an inductor (L).
2. Power Formula: The average power (P) in an AC circuit can be calculated using the formula:
P=Vrms×Irms×cosϕ
where:
- Vrms is the root mean square voltage,
- Irms is the root mean square current,
- ϕ is the phase difference between the voltage and current.
3. Phase Difference in Pure Inductance: In a pure inductive circuit, the voltage leads the current by 90 degrees. Therefore, the phase difference ϕ is 90 degrees.
4. Calculate Cosine of the Phase Angle: We need to find cos(90∘):
cos(90∘)=0
5. Substituting into the Power Formula: Now, substitute cos(90∘) into the power formula:
P=Vrms×Irms×0
6. Conclusion: Since any number multiplied by zero is zero, we find that:
P=0
Thus, the power dissipated in a pure inductance is zero.
Final Answer:
The power dissipated in pure inductance will be 0 watts.
---
P=Vrms×Irms×cosϕ
where:
- Vrms is the root mean square voltage,
- Irms is the root mean square current,
- ϕ is the phase difference between the voltage and current.
cos(90∘)=0
P=Vrms×Irms×0
P=0
Thus, the power dissipated in a pure inductance is zero.
The power dissipated in pure inductance will be 0 watts.
Similar Questions
Knowledge Check
A series circuit connected across a 200V,60Hz line consists of a capacitive reactance 30Ω non inductive resistor of 44Ω and a coil of inductive reactance 90Ω and resistance 36Ω as shown in the diagram
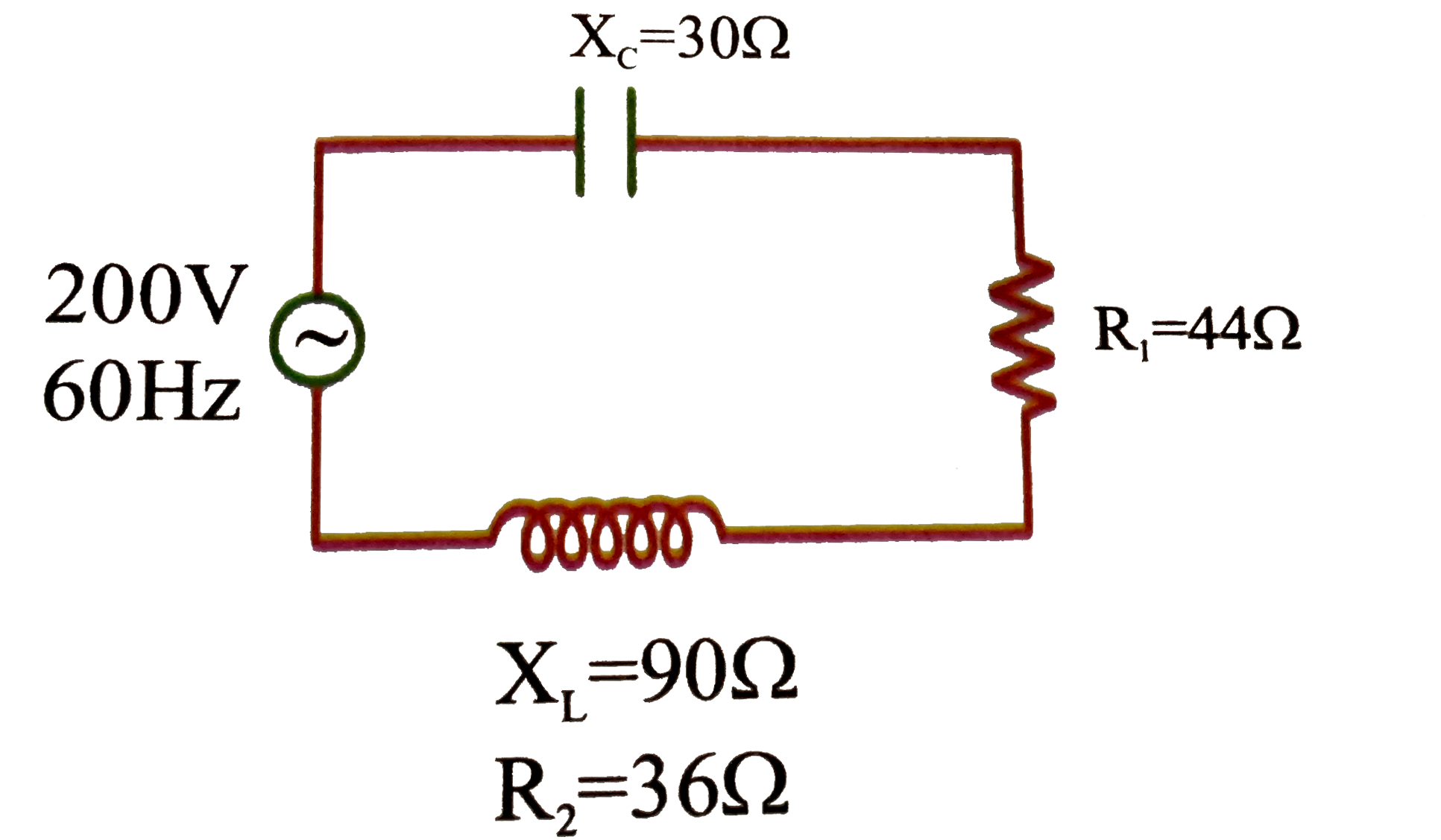
The power dissipated in the inductance coil isAzeroB320WC144WD160WThe average power is dissipated in a pure inductor is
AVI24B12VICzeroDVI2The average power dissipated in a pure inductor L carrying an alternating current of rms value I is .
A12LI2BLI2C14LI2Dzero
The power dissipated in the adjacent circuit is -
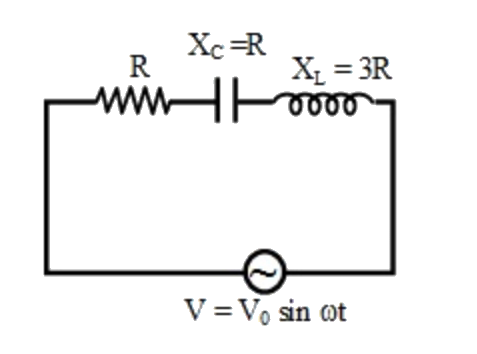
View SolutionThe power dissipated in 3Ω resistor in the circuits as shown in the figure is 2W. The power dissipated in 7Ω resistor will be
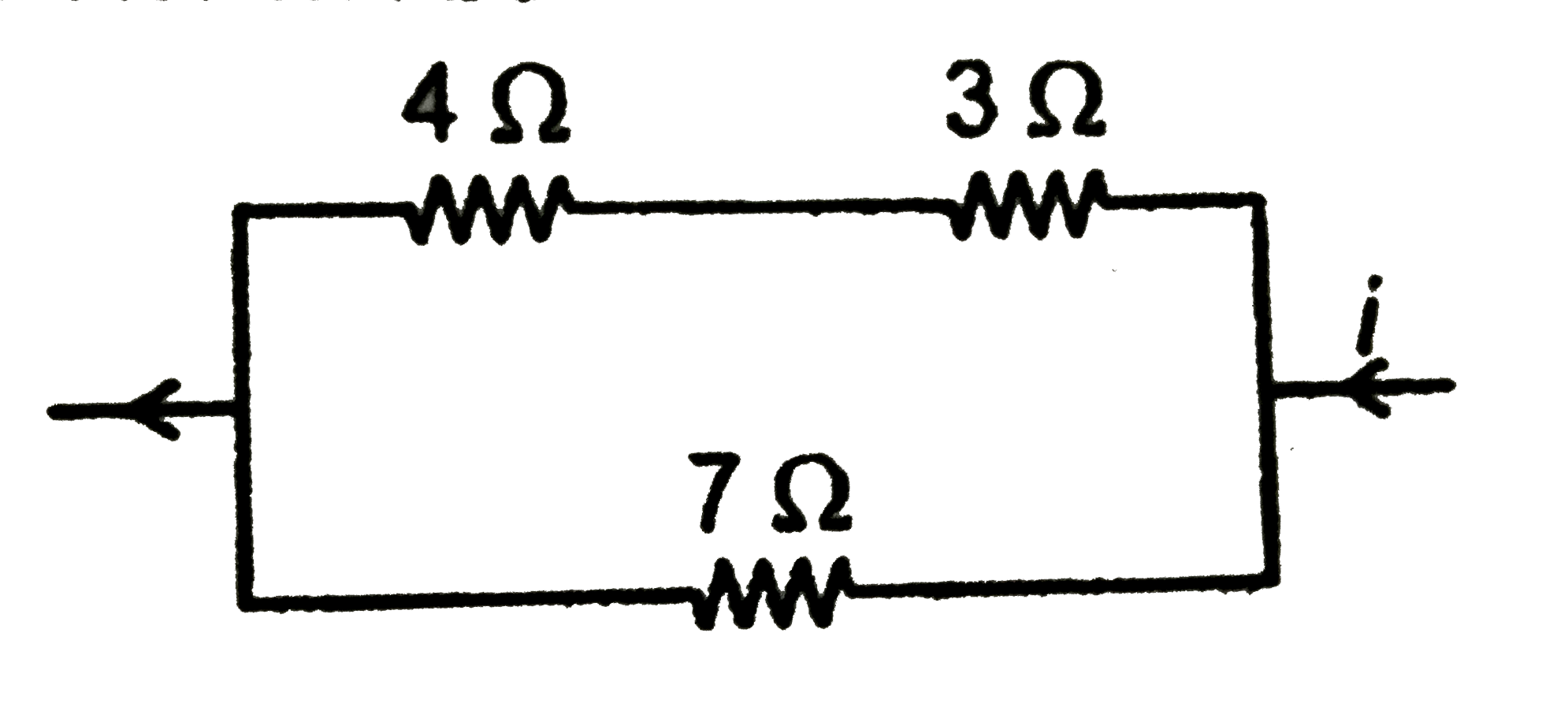
View SolutionAssertion : In a purely inductive or capacitive circuit, the current is referred to as wattless currents.
Reason : No power is dissipated in a purely inductive or capacitive circuit even though a current is flowing in the circuit.
View SolutionThe average power dissipation in a pure capacitance in AC circuit is
View SolutionFour equal resistance dissipated 5 W of power together when connected in series to a battery of negligible internal resistance . The total power dissipated in these resistance when connected in parallel across the same battery would be .
View Solution