For a series R-L-C circuit :-
(a) Voltage across L and C are differ by π
(b) Current through L and R are in same phase
(c) Voltage across R and L differ by π/2
(d) Voltage across L and current through C are differ by π/2
a,b,c
b,c,d
c,d,a
ALL
The correct Answer is:D
To solve the problem regarding the phase relationships in a series R-L-C circuit, let's analyze each of the given options step by step.
Step 1: Understanding the Phase Relationships
In a series R-L-C circuit:
- The current (I) is the same through all components (R, L, and C).
- The voltage across the resistor (V_R) is in phase with the current.
- The voltage across the inductor (V_L) leads the current by π/2 (90 degrees).
- The voltage across the capacitor (V_C) lags the current by π/2 (90 degrees).
Step 2: Analyzing Each Option
Now, let's analyze each of the options provided in the question:
Option (a): Voltage across L and C differ by π
- The voltage across the inductor (V_L) leads the current by π/2, and the voltage across the capacitor (V_C) lags the current by π/2.
- Therefore, the phase difference between V_L and V_C is π (180 degrees).
- Conclusion: This statement is correct.
Option (b): Current through L and R are in the same phase
- Since the circuit is in series, the current through the inductor (I_L) and the current through the resistor (I_R) are the same.
- Conclusion: This statement is correct.
Option (c): Voltage across R and L differ by π/2
- The voltage across the resistor (V_R) is in phase with the current, while the voltage across the inductor (V_L) leads the current by π/2.
- Therefore, the phase difference between V_R and V_L is π/2.
- Conclusion: This statement is correct.
Option (d): Voltage across L and current through C differ by π/2
- The voltage across the inductor (V_L) leads the current by π/2, while the current through the capacitor (I_C) lags the voltage across the capacitor (V_C) by π/2.
- Since V_L leads the current and I_C lags the voltage, the phase difference between V_L and I_C is indeed π/2.
- Conclusion: This statement is correct.
Final Conclusion
All four options are correct. Therefore, the answer is that all statements (a, b, c, d) are true.
In a series R-L-C circuit:
- The current (I) is the same through all components (R, L, and C).
- The voltage across the resistor (V_R) is in phase with the current.
- The voltage across the inductor (V_L) leads the current by π/2 (90 degrees).
- The voltage across the capacitor (V_C) lags the current by π/2 (90 degrees).
Now, let's analyze each of the options provided in the question:
- The voltage across the inductor (V_L) leads the current by π/2, and the voltage across the capacitor (V_C) lags the current by π/2.
- Therefore, the phase difference between V_L and V_C is π (180 degrees).
- Conclusion: This statement is correct.
- Since the circuit is in series, the current through the inductor (I_L) and the current through the resistor (I_R) are the same.
- Conclusion: This statement is correct.
- The voltage across the resistor (V_R) is in phase with the current, while the voltage across the inductor (V_L) leads the current by π/2.
- Therefore, the phase difference between V_R and V_L is π/2.
- Conclusion: This statement is correct.
- The voltage across the inductor (V_L) leads the current by π/2, while the current through the capacitor (I_C) lags the voltage across the capacitor (V_C) by π/2.
- Since V_L leads the current and I_C lags the voltage, the phase difference between V_L and I_C is indeed π/2.
- Conclusion: This statement is correct.
All four options are correct. Therefore, the answer is that all statements (a, b, c, d) are true.
Similar Questions
Knowledge Check
In series LCR circuit, the voltages across R, L and C are shown in the figure. The voltage of applied source
 A110 VB10 voltC50 voltD70 volt
A110 VB10 voltC50 voltD70 voltIn series LCR circuit, the voltages across R, L and C shown in figure. The voltage of applied source is
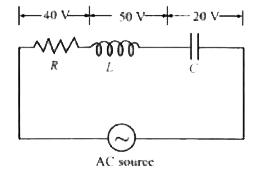 A110 voltB10 voltC50 voltD70 volt
A110 voltB10 voltC50 voltD70 voltPhase difference between voltages across L and C in series is
A0∘B90∘C180∘D360∘
In an LCR series circuit the voltages across R,L and C at resonance are 40Vand60V respectively the applied voltage is .
View SolutionConsider following series R-L-C circuit.
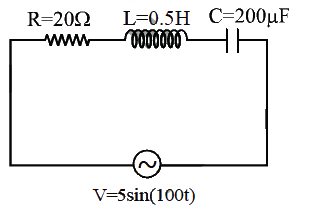
The maximum voltage drop across inductance is :-
View SolutionFor a series RLC circuit R=XL=2XC. The impedance of the current and phase different (between) V and i will be
View SolutionIn an LCR series circuit the rms voltages across R,L and C are foundd to be 10V,10V and 20V respectively. The rms voltage across the entire combination is
View SolutionIn series LCR circuit, the phase difference between voltage across L and voltage across C is
View Solution


