If instantaneous current in a circuit is given by I=(2+3sinωt) A, then the effective value of resulting current in the circuit is
√172A
√217A
√3√2A
3√2A
The correct Answer is:A
To find the effective (RMS) value of the instantaneous current given by I(t)=2+3sin(ωt) A, we can follow these steps:
Step 1: Define the RMS value
The effective (RMS) value of a current is defined as:
Irms=√1T∫T0I(t)2dt
where T is the time period of the current.
Step 2: Square the instantaneous current
We need to compute I(t)2:
I(t)=2+3sin(ωt)
Squaring this gives:
I(t)2=(2+3sin(ωt))2=4+12sin(ωt)+9sin2(ωt)
Step 3: Substitute into the RMS formula
Now, we substitute I(t)2 into the RMS formula:
Irms=√1T∫T0(4+12sin(ωt)+9sin2(ωt))dt
Step 4: Evaluate the integral
We can break this integral into three parts:
∫T0(4+12sin(ωt)+9sin2(ωt))dt=∫T04dt+∫T012sin(ωt)dt+∫T09sin2(ωt)dt
1. First Integral:
∫T04dt=4T
2. Second Integral:
The integral of sin(ωt) over one complete cycle is zero:
∫T012sin(ωt)dt=0
3. Third Integral:
For sin2(ωt), we use the identity:
sin2(ωt)=1−cos(2ωt)2
Thus,
∫T09sin2(ωt)dt=9∫T01−cos(2ωt)2dt=92(T−0)=9T2
Step 5: Combine the results
Now we can combine the results from the integrals:
∫T0(4+12sin(ωt)+9sin2(ωt))dt=4T+0+9T2=4T+9T2=8T2+9T2=17T2
Step 6: Substitute back into the RMS formula
Now substituting back into the RMS formula:
Irms=√1T⋅17T2=√172
Step 7: Final result
Thus, the effective value of the resulting current in the circuit is:
Irms=√172A
The effective (RMS) value of a current is defined as:
Irms=√1T∫T0I(t)2dt
where T is the time period of the current.
We need to compute I(t)2:
I(t)=2+3sin(ωt)
Squaring this gives:
I(t)2=(2+3sin(ωt))2=4+12sin(ωt)+9sin2(ωt)
Now, we substitute I(t)2 into the RMS formula:
Irms=√1T∫T0(4+12sin(ωt)+9sin2(ωt))dt
We can break this integral into three parts:
∫T0(4+12sin(ωt)+9sin2(ωt))dt=∫T04dt+∫T012sin(ωt)dt+∫T09sin2(ωt)dt
∫T04dt=4T
The integral of sin(ωt) over one complete cycle is zero:
∫T012sin(ωt)dt=0
For sin2(ωt), we use the identity:
sin2(ωt)=1−cos(2ωt)2
Thus,
∫T09sin2(ωt)dt=9∫T01−cos(2ωt)2dt=92(T−0)=9T2
Now we can combine the results from the integrals:
∫T0(4+12sin(ωt)+9sin2(ωt))dt=4T+0+9T2=4T+9T2=8T2+9T2=17T2
Now substituting back into the RMS formula:
Irms=√1T⋅17T2=√172
Thus, the effective value of the resulting current in the circuit is:
Irms=√172A
Similar Questions
Knowledge Check
A current in circuit is given by i = 3 + 4 sinωt. Then the effective value of current is :
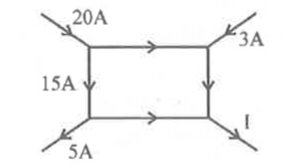
A5B√7C√17D√10The value of current I in the circuit will be
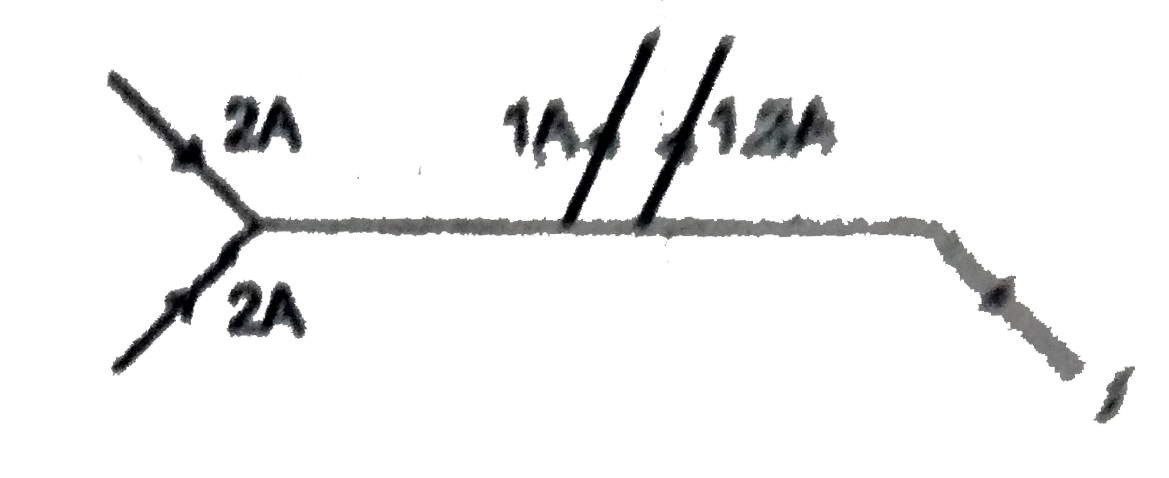 A1.7AB2.1AC3ADzero
A1.7AB2.1AC3ADzeroIf the instantaneous current in a circuit is given by I=20cos(ωt+ϕ)A, the rms value of the current is
A2AB√2AC2√2ADzero
If the instantaneous current in a circuit is given by I=2cos(ωt+ϕ) amperes, the rms value of the current is
View SolutionThe instantaneous current in an A.C. circuit is given by I=2sin(ωt+θ) ampere. The r.m.s. value of the current is
View SolutionThe current I in the given circuit is
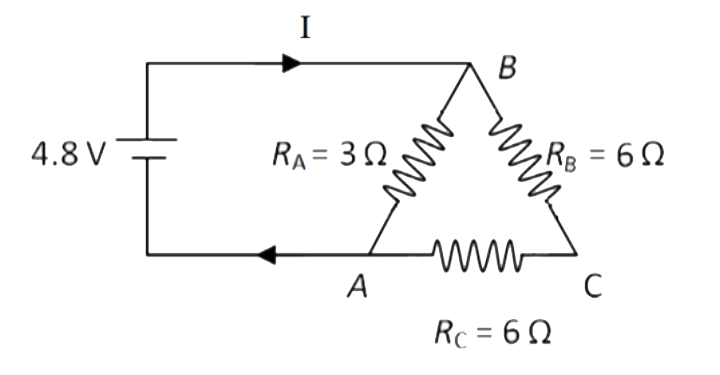
View SolutionIf the instantaneous current in a circuit is given by i=2cos(ωt−ϕ)ampere, the r.m.s. value of the current is
View SolutionValue of current i in the follwing circuit is:
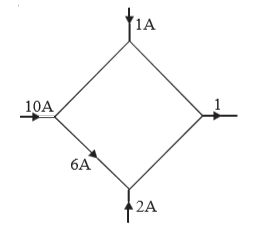
View Solution