The velocity of any particle is related with its displacement As, x=√v+1, Calculate acceleration at x=5m.
√6 unit
24 unit
240 unit
25 unit
x=√v+1⇒x2+v+1⇒v=x2−1
⇒dvdx=2x . Now acceleration
a=vdvdx=(x2−1).2x
This is the acceleration at position x. Now at x = 5 unit, a=(52−1)(2×5)=240 unit
Hence correct answer is (C).
Topper's Solved these Questions
- ONE DIMENSION MOTIONBOOK - MOTIONCHAPTER - ONE DIMENSION MOTIONEXERCISE - EXERCSE -1 (Section - A : Distance, Displacement, Velocity and Acceleration, Equation of Motion )
26 Videos
- ONE DIMENSION MOTIONBOOK - MOTIONCHAPTER - ONE DIMENSION MOTIONEXERCISE - EXERCSE -1 (Section - B : Motion under Gravity)
11 Videos
- NLM & FRICTIONBOOK - MOTIONCHAPTER - NLM & FRICTIONEXERCISE - EXERCISE-4 ( LEVEL-II)
15 Videos
- OPTICSBOOK - MOTIONCHAPTER - OPTICSEXERCISE - Exercise
45 Videos
Similar Questions
Knowledge Check
The velocity of a particle varies with its displacement as v=(√9−x2)ms−1.
Find the magnitude of the maximum acceleration of the particle.A3ms−2B4ms−2C3.5ms−2D5ms−2If the velocity v of particle moving along a straight line decreases linearly with its displacement s from 20ms−1 to a value approaching zero at s = 30 m, then acceleration of the particle at v=10ms^(-1) is
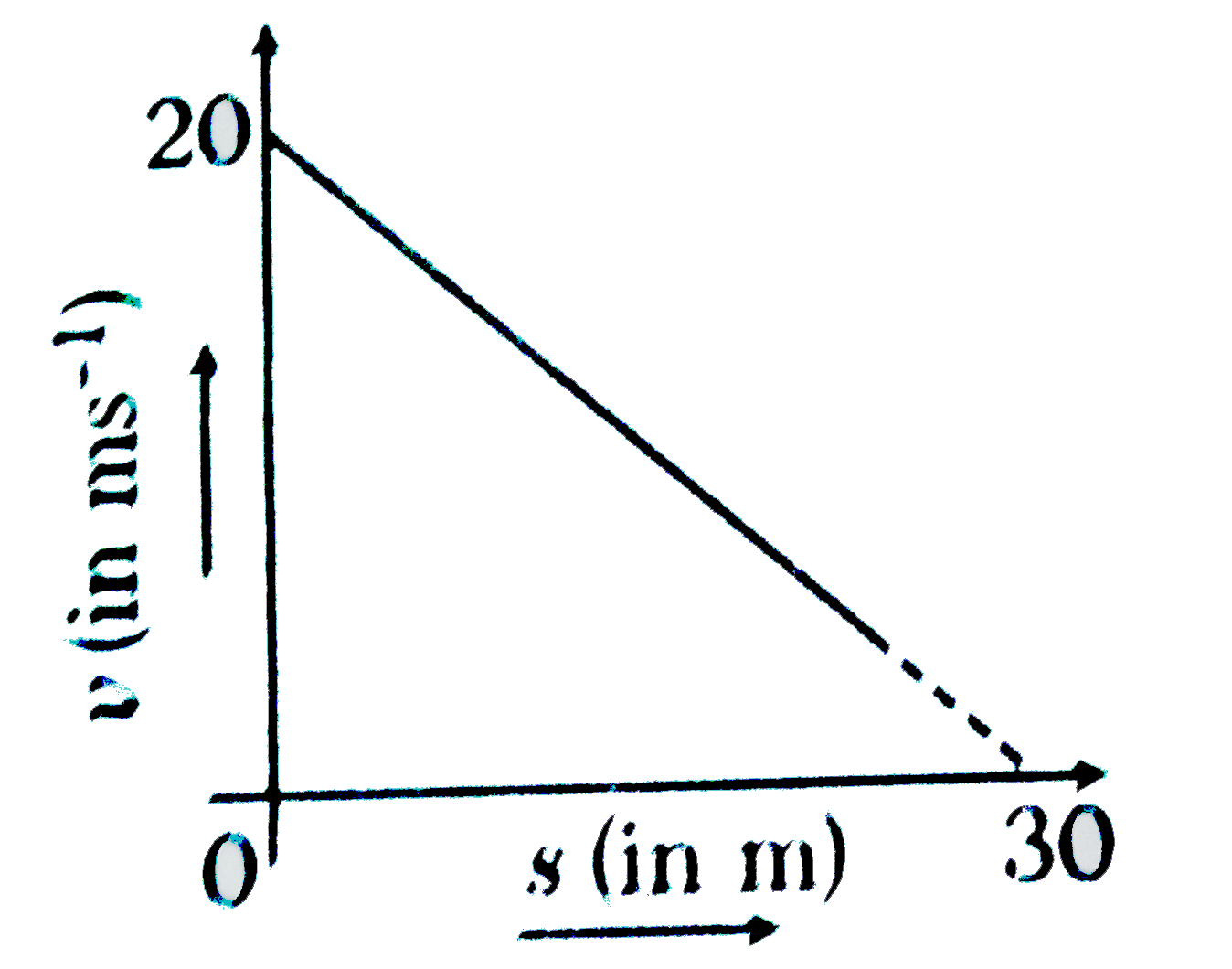 A23ms−2B−23ms−2C203ms−2D−203ms−2
A23ms−2B−23ms−2C203ms−2D−203ms−2
If the velocity of a body related to displacement x is given by v=√5000+24x m/s, then the acceleration of the body is _______m/s2.
View SolutionThe velocity v of moving object varies with displacement u as v=3x^(2)-2 ,then the acceleration at x=2m is
View SolutionIf v=√5000+24xms then calculate acceleration.
View SolutionVelocity of a particle moving in a straight line varies with its displacement as v=√4+4xm/s where x is displacement. Displacement of particle at time t = 0 is x = 0. Find displacement (in m) of particle in 2 sec.
View SolutionThe velocity of particle is given by v=√gx . Find its acceleration.
View SolutionThe velocity time relation of a particle is given by v =(3t2−2t−1)m/s Calculate the position and acceleration of the particle when velocity of the particle is zero . Given the initial position of the particle is 5m .
View Solution
