The self inductance of a toroid is :-
μ0N2r22Rm
μ0N2πr2Rm
μ0N2r2Rm
μ0N2rπrm
The correct Answer is:a
To find the self-inductance of a toroid, we can follow these steps:
1. Understanding the Geometry of the Toroid:
- A toroid is a doughnut-shaped coil of wire. We denote the radius from the center of the toroid to the center of the wire as R, and the radius of the wire itself as r.
2. Magnetic Field Inside the Toroid:
- The magnetic field B inside a toroid carrying a current I is given by the formula:
B=μ0IN2πR
where μ0 is the permeability of free space and N is the number of turns of the wire.
3. Calculating the Magnetic Flux:
- The magnetic flux Φ through one loop of the toroid can be expressed as:
Φ=B⋅A
where A is the cross-sectional area of the toroid. For a circular cross-section, the area A can be calculated as:
A=πr2
Therefore, the total magnetic flux through N turns is:
Φtotal=N⋅B⋅A=N⋅(μ0IN2πR)⋅(πr2)
4. Relating Flux to Inductance:
- The self-inductance L is defined by the relationship:
Φtotal=L⋅I
Substituting the expression for total magnetic flux:
N⋅(μ0IN2πR)⋅(πr2)=L⋅I
5. Solving for Self-Inductance L:
- We can cancel I from both sides (assuming I≠0):
L=N2μ0r22πR
6. Final Expression for Self-Inductance:
- Thus, the self-inductance of a toroid is given by:
L=μ0N2r22πR
Summary:
The self-inductance of a toroid is:
L=μ0N2r22πR
- A toroid is a doughnut-shaped coil of wire. We denote the radius from the center of the toroid to the center of the wire as R, and the radius of the wire itself as r.
- The magnetic field B inside a toroid carrying a current I is given by the formula:
B=μ0IN2πR
where μ0 is the permeability of free space and N is the number of turns of the wire.
- The magnetic flux Φ through one loop of the toroid can be expressed as:
Φ=B⋅A
where A is the cross-sectional area of the toroid. For a circular cross-section, the area A can be calculated as:
A=πr2
Therefore, the total magnetic flux through N turns is:
Φtotal=N⋅B⋅A=N⋅(μ0IN2πR)⋅(πr2)
- The self-inductance L is defined by the relationship:
Φtotal=L⋅I
Substituting the expression for total magnetic flux:
N⋅(μ0IN2πR)⋅(πr2)=L⋅I
- We can cancel I from both sides (assuming I≠0):
L=N2μ0r22πR
- Thus, the self-inductance of a toroid is given by:
L=μ0N2r22πR
The self-inductance of a toroid is:
L=μ0N2r22πR
Topper's Solved these Questions
- ELECTRO MAGNETIC INDUCTIONBook:MOTIONChapter:ELECTRO MAGNETIC INDUCTIONExercise:EXERCISE-3 (Assertion & Reasoning)
Explore 18 Videos
- ELECTRO MAGNETIC INDUCTIONBook:MOTIONChapter:ELECTRO MAGNETIC INDUCTIONExercise:EXERCISE-4| Section A (Prevous Years Problems )
Explore 28 Videos
- ELECTRO MAGNETIC INDUCTIONBook:MOTIONChapter:ELECTRO MAGNETIC INDUCTIONExercise:EXERCISE-1
Explore 72 Videos
- Electrical Instrument Book:MOTIONChapter:Electrical Instrument Exercise:EXERCISE -3
Explore 16 Videos
- ELECTRO MAGNETIC WAVES Book:MOTIONChapter:ELECTRO MAGNETIC WAVES Exercise:EXERCISE - 3 (SECTION - B)
Explore 8 Videos
Similar Questions
A toroid is wound over a circular core. Radius of each turn is r and radius of toroid is R(>>r). The Coefficient of self - inductance of the toroid is given by
View SolutionFind the self-inductance of a toroidal solenoid of radius 20 cm, area of cross section 100cm2 and having 500 turns. Assume that the field variations across the cross section of the toroid are negligible. Further, if a secondary coil of 300 turns is wound on this toroid and the current in the primary coil is increased from 2 A to 5 A in 0.05 s. Find the emf induced in the secondary coil.
View Solution
Knowledge Check
A toroidal solenoid with an air core has an average radius of 15 cm , area of cross-section 12cm2 and 1200 turns . Ignoring the field variation across the cross-section of the toroid the self-inductance of the toroid is
A4.6 mHB6.9 mHC2.3 mHD9.2 mHThe self inductance of a coil is a measure of
Aelectrical inertiaBelectrical frictionCinduced emf and the magnetic fluxDinduced currentA toroid is wound over a circular core. Radius of each turn is r and radius of toroid is R(>>r). The coefficient of self-inductance of the toroid is given by
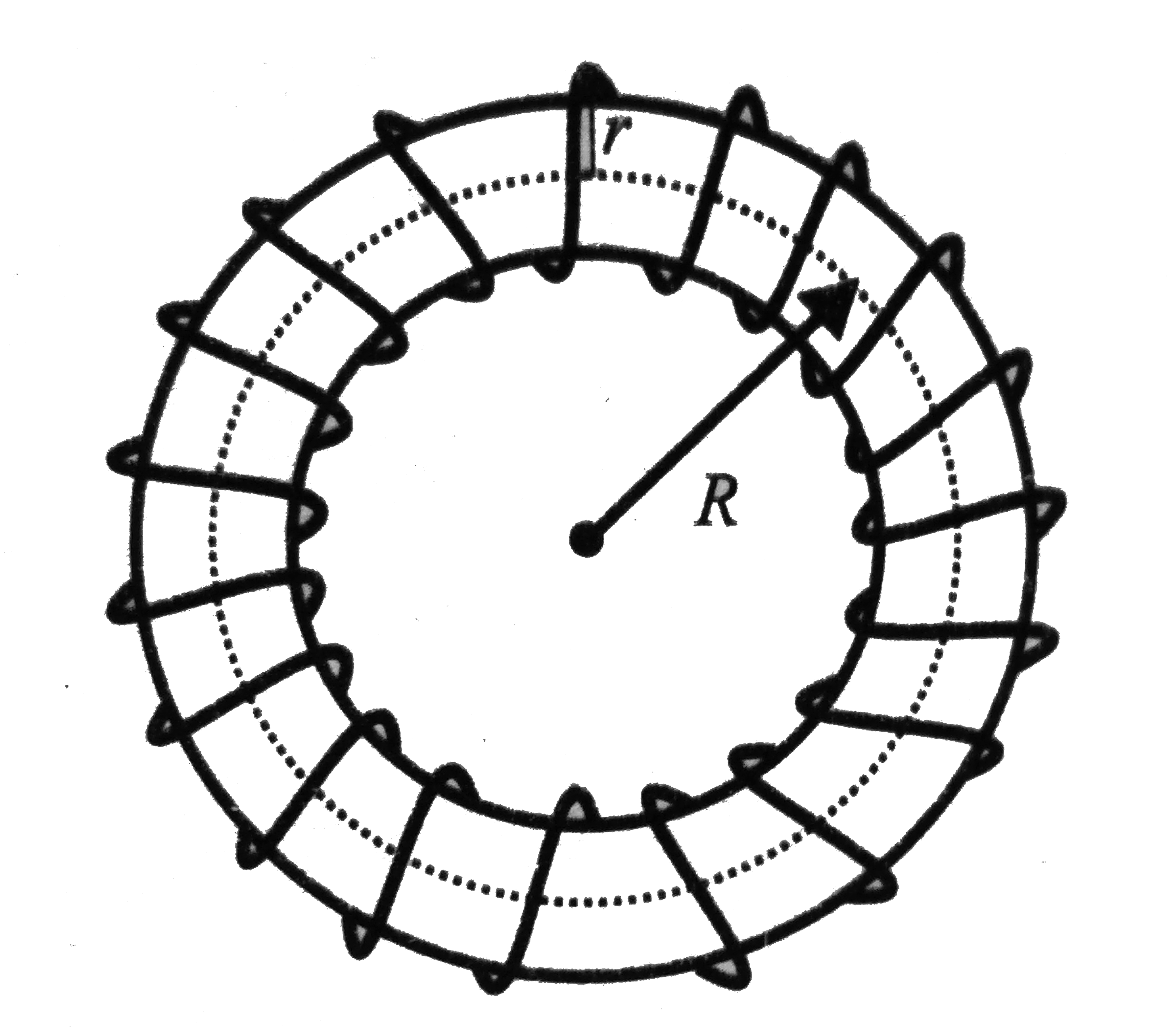 AL=μ0Nr22RBL=μ0Nr2RCL=μ0Nr2RDL=μ0N2r22R
AL=μ0Nr22RBL=μ0Nr2RCL=μ0Nr2RDL=μ0N2r22R
A toroidal solenoid with an air core has an average radius of 15 cm, area of cross-section 12cm2 and 1200 turns. Obtain the self inductance of the toroid. Ignore field variations across the cross-section of the toroid.
(b) A second coil of 300 turns is wound closely on the toroid above. If the current in the primary coil is increased from zero to 2.0 A in 0.05 s, obtain the induced e.m.f. in the second coil.
View SolutionA toroid of 1000 turns has an average radius of 10 cm and area of cross section 15cm2. Calculate the self-inductance of the toroid.
View SolutionThe self inductance of a coil does not depend upon
View SolutionThe coefficient of self inductance of a coil is
View SolutionThe unit of self inductance of a coil is
View Solution

