If the current in a primary circuit is I=I0 Sin ωt and the mutual inductance is M, then the value of induced voltage in secondary circuit will be :-
e=MI0ωCosωt
e=MI0ωCostωt
e=[MωCosωt]/I0
e=(MωCosωt)/I0
The correct Answer is:B
To find the induced voltage in the secondary circuit when the current in the primary circuit is given by I=I0sin(ωt) and the mutual inductance is M, we can follow these steps:
Step 1: Understand the relationship between current and induced voltage
The induced voltage (or electromotive force, EMF) in the secondary circuit due to a changing current in the primary circuit is given by the formula:
E=MdIdt
where E is the induced voltage, M is the mutual inductance, and dIdt is the rate of change of current in the primary circuit.
Step 2: Differentiate the current function
The current in the primary circuit is given by:
I=I0sin(ωt)
To find dIdt, we differentiate I with respect to t:
dIdt=I0ddt(sin(ωt))=I0ωcos(ωt)
Here, we used the chain rule where the derivative of sin(x) is cos(x) and multiplied by the derivative of ωt which is ω.
Step 3: Substitute dIdt into the induced voltage formula
Now, we substitute dIdt back into the formula for induced voltage:
E=MdIdt=M(I0ωcos(ωt))
This simplifies to:
E=MI0ωcos(ωt)
Step 4: Final expression for the induced voltage
Thus, the induced voltage in the secondary circuit is:
E=MI0ωcos(ωt)
Conclusion
The value of the induced voltage in the secondary circuit is MI0ωcos(ωt).
---
The induced voltage (or electromotive force, EMF) in the secondary circuit due to a changing current in the primary circuit is given by the formula:
E=MdIdt
where E is the induced voltage, M is the mutual inductance, and dIdt is the rate of change of current in the primary circuit.
The current in the primary circuit is given by:
I=I0sin(ωt)
To find dIdt, we differentiate I with respect to t:
dIdt=I0ddt(sin(ωt))=I0ωcos(ωt)
Here, we used the chain rule where the derivative of sin(x) is cos(x) and multiplied by the derivative of ωt which is ω.
Now, we substitute dIdt back into the formula for induced voltage:
E=MdIdt=M(I0ωcos(ωt))
This simplifies to:
E=MI0ωcos(ωt)
Thus, the induced voltage in the secondary circuit is:
E=MI0ωcos(ωt)
The value of the induced voltage in the secondary circuit is MI0ωcos(ωt).
Topper's Solved these Questions
- ELECTRO MAGNETIC INDUCTIONBook:MOTIONChapter:ELECTRO MAGNETIC INDUCTIONExercise:EXERCISE-1
Explore 72 Videos
- ELECTRO MAGNETIC INDUCTIONBook:MOTIONChapter:ELECTRO MAGNETIC INDUCTIONExercise:EXERCISE-2 (Objective problems (Analytical questions))
Explore 70 Videos
- ELECTRO MAGNETIC INDUCTIONBook:MOTIONChapter:ELECTRO MAGNETIC INDUCTIONExercise:QUESTIONS FOR PRACTICE (Type- IV: Questions based on induced Parameters :-)
Explore 10 Videos
- Electrical Instrument Book:MOTIONChapter:Electrical Instrument Exercise:EXERCISE -3
Explore 16 Videos
- ELECTRO MAGNETIC WAVES Book:MOTIONChapter:ELECTRO MAGNETIC WAVES Exercise:EXERCISE - 3 (SECTION - B)
Explore 8 Videos
Similar Questions
The value of the current I in the given circuit is
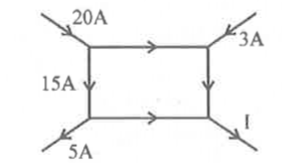
View SolutionIf the current in the primary circuit of a pair of coils changes from 5 A to 1 A in 0.02 s.
Calculate (i) induced emf in the secondary coil if the mutal inductance between the two coills is 0.5 H and
(ii) the change of flux per turn in the secondary ,if it has 200 turns .
View Solution
Knowledge Check
The value of current I in the circuit will be
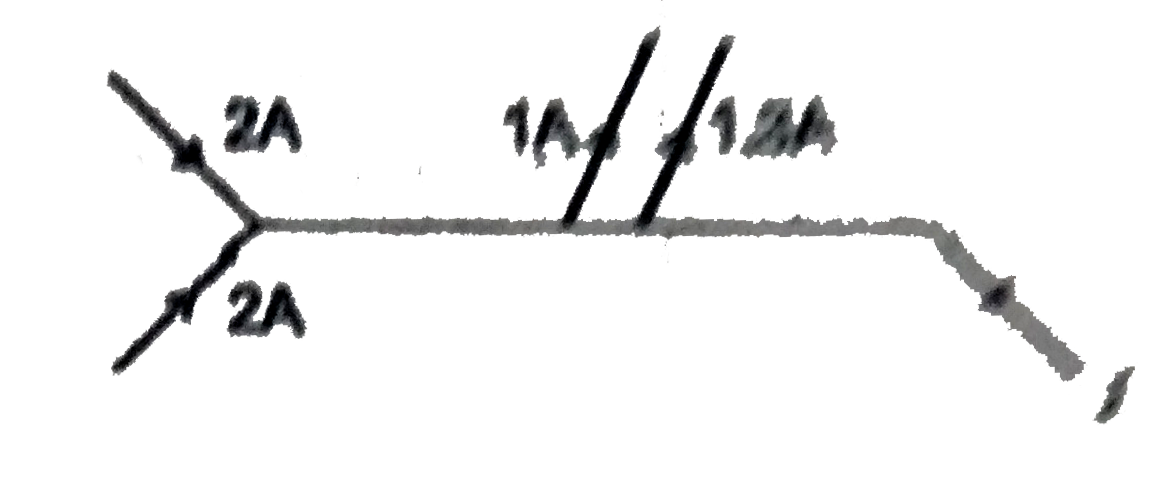 A1.7AB2.1AC3ADzero
A1.7AB2.1AC3ADzeroA current of 10A in the primary coil of a circuit is reduced to zero. If the coefficient of mutual inductance is 3 H and emf induced in the secondary coil is 30 kV, time taken for the change of current is
A103sB102sC10−3sD10−2sIf instantaneous current in a circuit is given by I=(2+3sinωt) A, then the effective value of resulting current in the circuit is
A√172AB√217AC√3√2AD3√2A
Find the value of current I in the circuit
View SolutionTwo coils have mutual inductance of 1.5 henry. If current in primary circuit is raised to 5 ampere in one millisecond after closing the circuit, what is the e.m.f. Induced in the secondary ?
View SolutionIf the current in the primary circuit of a pair of coils changes from 10 A to 0 in 0.1 s, calculate (i) the induced emf in the secondary if the mutual inductance between the two coils is 2 H and (ii) the change of flux per turn in the secondary if it has 500 turns.
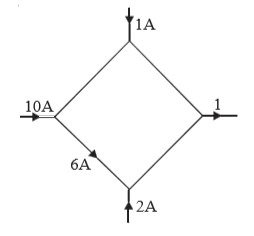
View SolutionValue of current i in the follwing circuit is:
View SolutionThe instantaneous current in a circuit is, I=sin(ωt+ϕ) ampere. What is the r.m.s., value of the current?
View Solution

