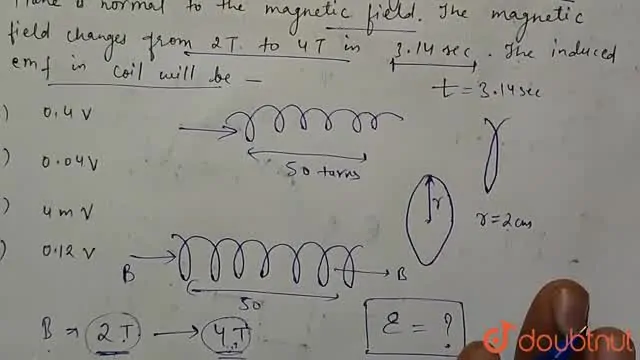
The radius of a circular coil having 50 turns is 2 cm. Its plane is normal to the magnetic field. The magnetic field changes from 2T to 4T in 3.14 sec. The induced emf in coil will be :-
0.4V
0.04V
4mV
0.12V
The correct Answer is:B
Step by step video, text & image solution for The radius of a circular coil having 50 turns is 2 cm. Its plane is normal to the magnetic field. The magnetic field changes from 2T to 4T in 3.14 sec. The induced emf in coil will be :- by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - MOTIONCHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - QUESTION FOR PRACTICE41videos
ELECTRO MAGNETIC INDUCTION
- BOOK - MOTIONCHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - EXERCISE-172videos
ELECTRO MAGNETIC INDUCTION
- BOOK - MOTIONCHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - QUESTIONS FOR PRACTICE (Type-III: Special Question :-)2videos
ELECTRO MAGNETIC INDUCTION
- BOOK - MOTIONCHAPTER - Electrical Instrument EXERCISE - EXERCISE -316videos
Electrical Instrument
- BOOK - MOTIONCHAPTER - ELECTRO MAGNETIC WAVES EXERCISE - EXERCISE - 3 (SECTION - B)8videos
ELECTRO MAGNETIC WAVES
Similar Questions
The radius of a circular coil having 100 turns is 2 cm. its plane is normal to the magnetic field.
The magnetic field changes from 4T to 8T in 3.14 sec. The induced emf in coil will beView SolutionThe radius of a circular coil having 100 turns is 5 cm .its plane is normal to the magnetic field. The magnetic field changes from 2T to 10 T in 3.14 sec. The induced emf in coil will be
View SolutionA coil having an area A0 is placed in a magnetic field which changes from B0 to 4B0 in time interval t. The emf induced in the coil will be
View SolutionA coil having an area A0 is placed in a magnetic field which changes from B0 to 4B0 in a time interval t. The e.m.f. induced in the coil will be
View SolutionA coil having an area A0 is placed in a magnetic field which changes from B0 to 4B0 in a time interval t. The e.m.f. induced in the coil will be
View SolutionA coil having an area A0 is placed in a magnetic field which changes from B0 to 4B0 in time interval t. The emf induced in the coil will be
View SolutionA coil having 100 turns and area 0.020m2 is placed normally in a magnetic field. The magnetic field changes from 0.20Wbm−2 at a uniform rate over a period of 0.01 s. Calculate the induced emf in the coil.
View SolutionA coil having n turns and area A is initially placed with its plane normal to the magnetic field B. It is then rotated through 180∘ in 0.2 sec. The emf induced at the ends of the coils is ___
View SolutionA coil of 50 turns and 4cm radius carries 2A current then magnetic field at its centre is :- ?
View SolutionA 50 turns circular coil has a radius of 3cm , it is kept in a magnetic field acting normal to the area of the coil. The magnetic field B increased from 0.10 tesla to 0.35 tesla in 2 milliseconds . The average induced e.m.f. in the coil is
View Solution