A cubical block rests on a plane of μ=√3 . The angle through which the plane be inclined to the horizontal so that the block just slides down will be -
30∘
45∘
60∘
75∘
The correct Answer is:C
To solve the problem of determining the angle at which a cubical block will just start to slide down an inclined plane with a coefficient of friction (μ) equal to √3, we can follow these steps:
Step 1: Understand the Forces Acting on the Block
When the block is placed on the inclined plane, two main forces act on it:
- The gravitational force (weight) acting downwards, which can be represented as mg.
- The normal force acting perpendicular to the surface of the inclined plane.
Step 2: Resolve the Gravitational Force
The gravitational force can be resolved into two components:
- A component parallel to the incline: mgsinθ
- A component perpendicular to the incline: mgcosθ
Step 3: Write the Expression for Normal Force
The normal force (N) acting on the block is equal to the perpendicular component of the gravitational force:
N=mgcosθ
Step 4: Determine the Maximum Static Friction
The maximum static friction force (F_friction) that can act on the block before it starts sliding is given by:
Ffriction=μN=μ(mgcosθ)
Step 5: Set Up the Condition for Sliding
The block will just start to slide when the component of the gravitational force parallel to the incline equals the maximum static friction force:
mgsinθ=μ(mgcosθ)
Step 6: Simplify the Equation
We can cancel mg from both sides (assuming mg≠0):
sinθ=μcosθ
Step 7: Divide Both Sides by cosθ
This gives us:
tanθ=μ
Step 8: Substitute the Value of μ
Given that μ=√3:
tanθ=√3
Step 9: Find the Angle θ
To find θ, we take the arctangent (inverse tangent) of both sides:
θ=tan−1(√3)
Step 10: Calculate θ
From trigonometric values, we know:
tan60∘=√3
Thus,
θ=60∘
Final Answer
The angle through which the plane can be inclined to the horizontal so that the block just slides down is 60∘.
---
When the block is placed on the inclined plane, two main forces act on it:
- The gravitational force (weight) acting downwards, which can be represented as mg.
- The normal force acting perpendicular to the surface of the inclined plane.
The gravitational force can be resolved into two components:
- A component parallel to the incline: mgsinθ
- A component perpendicular to the incline: mgcosθ
The normal force (N) acting on the block is equal to the perpendicular component of the gravitational force:
N=mgcosθ
The maximum static friction force (F_friction) that can act on the block before it starts sliding is given by:
Ffriction=μN=μ(mgcosθ)
The block will just start to slide when the component of the gravitational force parallel to the incline equals the maximum static friction force:
mgsinθ=μ(mgcosθ)
We can cancel mg from both sides (assuming mg≠0):
sinθ=μcosθ
This gives us:
tanθ=μ
Given that μ=√3:
tanθ=√3
To find θ, we take the arctangent (inverse tangent) of both sides:
θ=tan−1(√3)
From trigonometric values, we know:
tan60∘=√3
Thus,
θ=60∘
The angle through which the plane can be inclined to the horizontal so that the block just slides down is 60∘.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION & FRICTION Book:MOTIONChapter:NEWTON'S LAWS OF MOTION & FRICTION Exercise:Exercise - 2 SECTION-A:- String Constrained, Wedge Constrained, Newtons Law theory Question, Equillibrium Questions (Normal and Tension), Problems with Acceleration (F=ma), Wedge problems
Explore 23 Videos
- NEWTON'S LAWS OF MOTION & FRICTION Book:MOTIONChapter:NEWTON'S LAWS OF MOTION & FRICTION Exercise:Exercise - 2 SECTION-B :- Pulley Block System
Explore 7 Videos
- NEWTON'S LAWS OF MOTION & FRICTION Book:MOTIONChapter:NEWTON'S LAWS OF MOTION & FRICTION Exercise:Exercise - 1 SECTION-E:- Static friction, Kinetic friction
Explore 13 Videos
- MODERN PHYSICS -1Book:MOTIONChapter:MODERN PHYSICS -1Exercise:EXERCISE-4 ( LEVEL- II)
Explore 39 Videos
- NLM & FRICTIONBook:MOTIONChapter:NLM & FRICTIONExercise:EXERCISE-4 ( LEVEL-II)
Explore 15 Videos
Similar Questions
A cubical block rests on an inclined plance of μ=1√3 . Determine the angle at which the block just slides down the incline .
View SolutionThe coefficient of static friction between a block of mass m and an incline is μs=03, a. What can be the maximum angle θ of the incline with the horizontal so that the block does not slip on the plane? b. If the incline makes an angle θ2 with the horizontal, find the frictional force on the block.
View Solution
Knowledge Check
A cubical block rests on a plane of μ=√3 . The angle through which the plane be inclined to the horizontal so that the block just slides down will be -
A30∘B45∘C60∘D75∘A cubical block rests on an inclined plane of coefficient of friction μ=1√3 . What should be the angle of inclination so that the block just slides down the inclined plane?
A30∘B60∘C45∘D90∘The angle which the rough inclined plane makes with the horizontal when the body placed on it just starts sliding down is called
Aangle of FrictionBangle of reposeCcritical angleDbrewster's angle
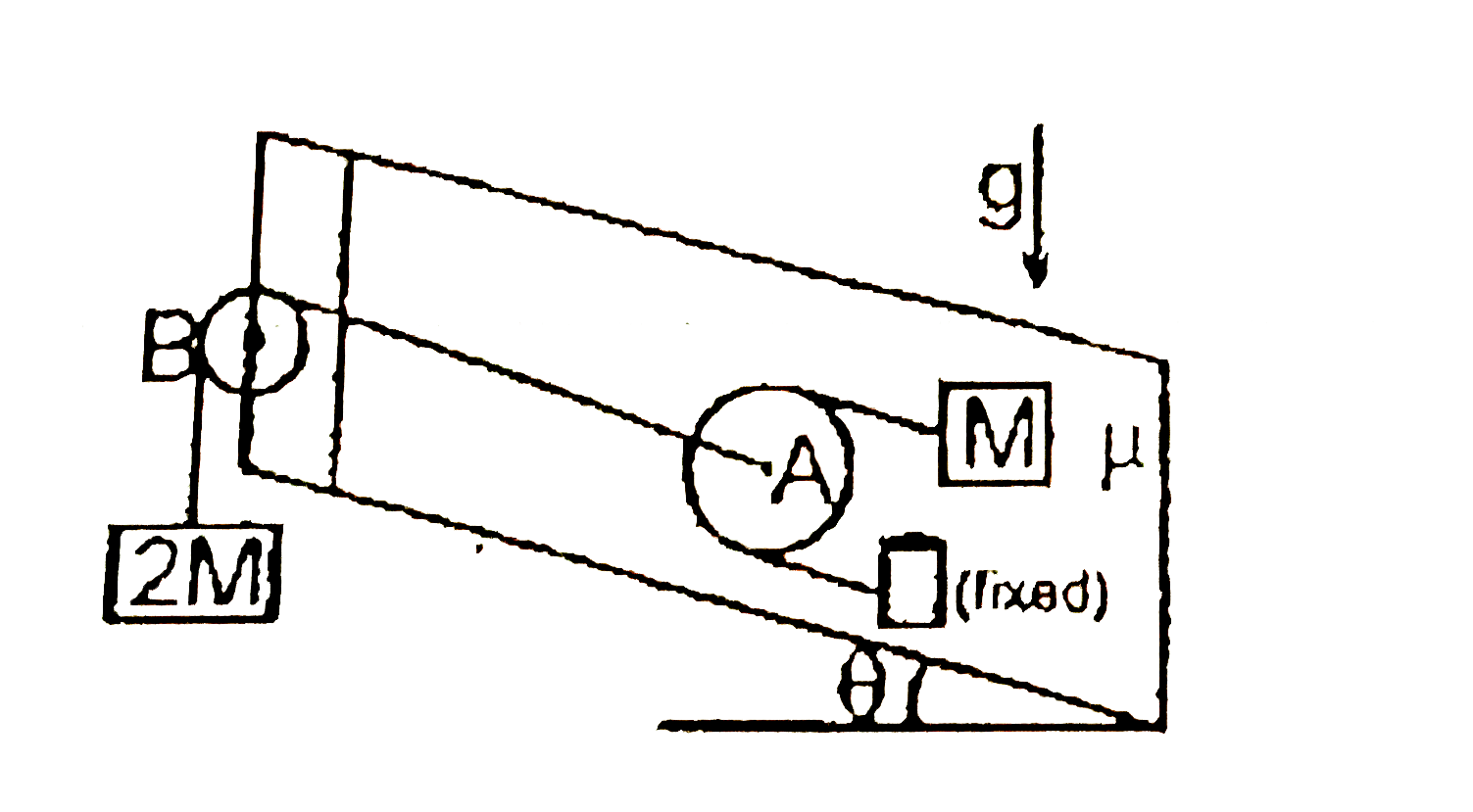
A block of mass M sits on an inclined plane and is connected via a massless string through a massless pulley A that slides without friction on the plane to a fixed post. This pulley is in turn connected via a massless string through a second massless pulley B to a second block of mass 2M that hangs above the ground. The coefficient of static friction between the inclined plane and block resting on the inclined plane is μ. The inclined plane is tilted to an anlge θ w.r.t. horizontal, so the blocks just start to move. Find the value of quantity μcosθ+sinθ.
View SolutionThe angle which the rough inclined plane makes with the horizontal when the body placed on it just starts sliding down is called .
View SolutionA block of mass m rests on a rough inclined plane. The coefficient of friction between the surface and the block is µ. At what angle of inclination θ of the plane to the horizontal will the block just start to slide down the plane?
View SolutionA block mass 'm' is placed on a frictionless inclined plane of inclination θ with horizontal. The inclined plane is accelerated horizontally so that the block does not slide down. In this situation vertical force exerted by the inclined plane on the block is:
View SolutionA block of mass m is placed on a rough inclined plane. When the inclination of the plane is θ , the block just beging to slide down the plane under its own weight. The minimum force applied parallel to the plane, to move the block up the plane, is.
View Solution