A lift is moving up with an acceleration of 3.675 m/sec2. The weight of a man-
increases by 37.5%
decreases by37.5%
increases by 137.5%
remains the same
The correct Answer is:A
To solve the problem of how the weight of a man changes when a lift accelerates upwards, we can follow these steps:
1. Understand the Forces Acting on the Man:
- When the lift is stationary or moving at constant velocity, the only forces acting on the man are his weight (downward force) and the normal force (upward force) exerted by the lift floor.
- The weight of the man is given by W=mg, where m is the mass of the man and g is the acceleration due to gravity (approximately 9.8m/s2).
2. Identify the Situation with Upward Acceleration:
- When the lift accelerates upwards with an acceleration a=3.675m/s2, the effective weight of the man increases.
- The normal force N acting on the man can be expressed as:
N=mg+ma
- Here, mg is the weight of the man, and ma is the additional force due to the lift's upward acceleration.
3. Calculate the Normal Force:
- Substitute the values into the equation for normal force:
N=m(g+a)=m(9.8+3.675)
- This simplifies to:
N=m(13.475)N
4. Calculate the Percentage Increase in Weight:
- The original weight of the man is mg=m×9.8.
- The increase in weight due to the lift's acceleration is:
ΔW=N−mg=m(13.475)−m(9.8)=m(3.675)
- The percentage increase in weight is given by:
Percentage Increase=(ΔWmg)×100=(m(3.675)m(9.8))×100
- The mass m cancels out:
Percentage Increase=(3.6759.8)×100
5. Perform the Calculation:
- Calculate the fraction:
3.6759.8≈0.3745
- Convert to percentage:
0.3745×100≈37.45%
6. Conclusion:
- The weight of the man increases by approximately 37.5% when the lift accelerates upwards at 3.675m/s2.
Final Answer:
The weight of the man increases by approximately 37.5%.
- When the lift is stationary or moving at constant velocity, the only forces acting on the man are his weight (downward force) and the normal force (upward force) exerted by the lift floor.
- The weight of the man is given by W=mg, where m is the mass of the man and g is the acceleration due to gravity (approximately 9.8m/s2).
- When the lift accelerates upwards with an acceleration a=3.675m/s2, the effective weight of the man increases.
- The normal force N acting on the man can be expressed as:
N=mg+ma
- Here, mg is the weight of the man, and ma is the additional force due to the lift's upward acceleration.
- Substitute the values into the equation for normal force:
N=m(g+a)=m(9.8+3.675)
- This simplifies to:
N=m(13.475)N
- The original weight of the man is mg=m×9.8.
- The increase in weight due to the lift's acceleration is:
ΔW=N−mg=m(13.475)−m(9.8)=m(3.675)
- The percentage increase in weight is given by:
Percentage Increase=(ΔWmg)×100=(m(3.675)m(9.8))×100
- The mass m cancels out:
Percentage Increase=(3.6759.8)×100
- Calculate the fraction:
3.6759.8≈0.3745
- Convert to percentage:
0.3745×100≈37.45%
- The weight of the man increases by approximately 37.5% when the lift accelerates upwards at 3.675m/s2.
The weight of the man increases by approximately 37.5%.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION & FRICTION Book:MOTIONChapter:NEWTON'S LAWS OF MOTION & FRICTION Exercise:Exercise - 1 SECTION-D :- Spring force and spring cutting problems
Explore 7 Videos
- NEWTON'S LAWS OF MOTION & FRICTION Book:MOTIONChapter:NEWTON'S LAWS OF MOTION & FRICTION Exercise:Exercise - 1 SECTION-E:- Static friction, Kinetic friction
Explore 13 Videos
- NEWTON'S LAWS OF MOTION & FRICTION Book:MOTIONChapter:NEWTON'S LAWS OF MOTION & FRICTION Exercise:Exercise - 1 SECTION-B :- Pulley Block System
Explore 12 Videos
- MODERN PHYSICS -1Book:MOTIONChapter:MODERN PHYSICS -1Exercise:EXERCISE-4 ( LEVEL- II)
Explore 39 Videos
- NLM & FRICTIONBook:MOTIONChapter:NLM & FRICTIONExercise:EXERCISE-4 ( LEVEL-II)
Explore 15 Videos
Similar Questions
A lift is moving upwards with an acceleration of 2m/sec2. Inside the lift a 4kg block is kept on the floor. On the top of it , 3kg block is placed and again a 2kg block is kept on the 3kg . Calculator :
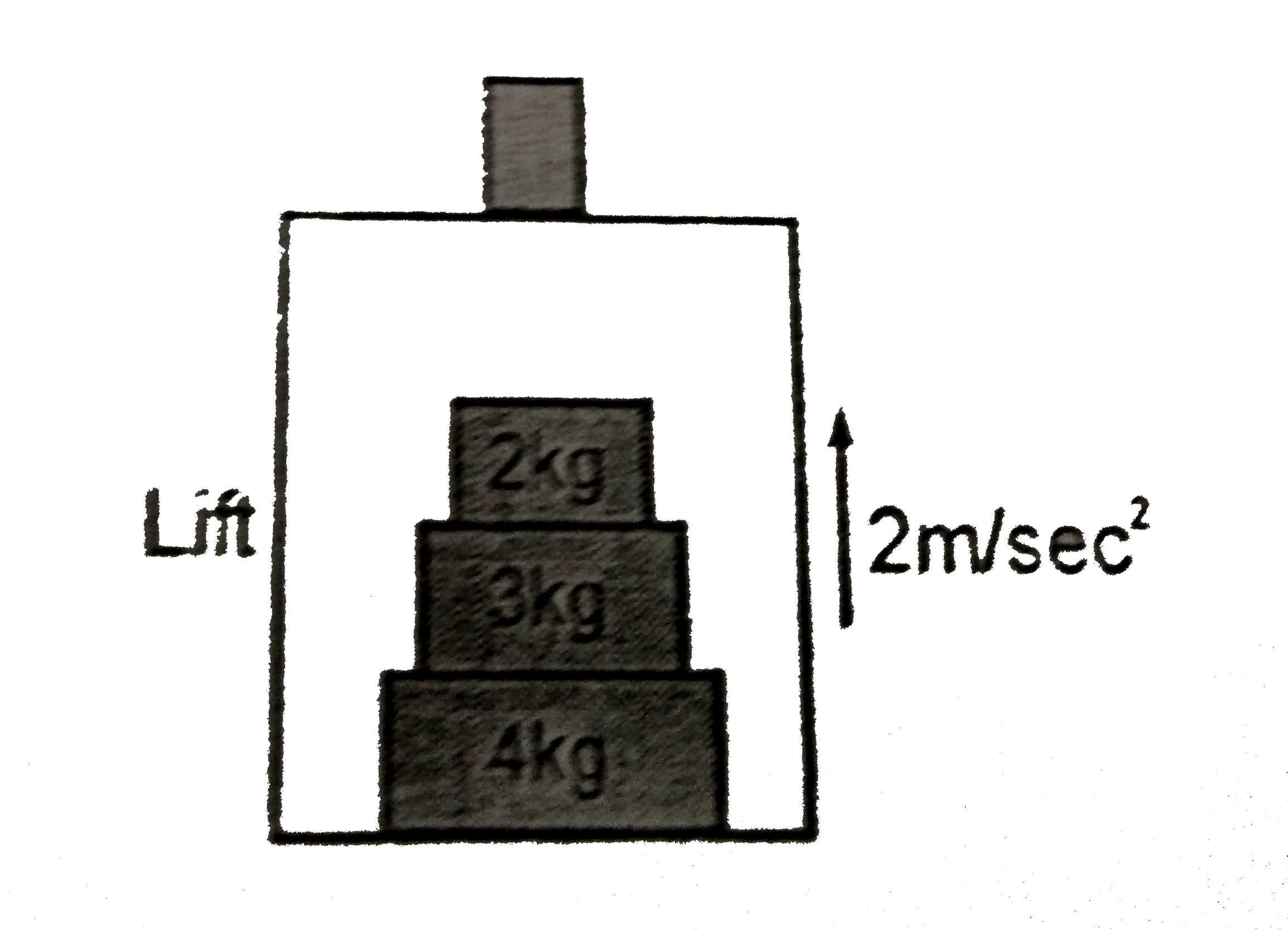
(i) contact force between 2kg block and the 3kg block.
(ii) contact force between 4kg block and floor of the lift.
Draw the free body diagrams properly & take g=10m/sec2
View SolutionA man weighs 80 kg. He stands on a weighing scale in a lift which is moving upwards with a uniform acceleration of 5m/s2. What would be the reading on the scale? (g=10m/s2)
View Solution
Knowledge Check
A man of weight W is standing on a lift which is moving upward with an acceleration a. The apparent weight of the man is
AW(1+ag)BWCW(1−ag)DW(1−a2g2)A 60kg man is inside a lift which is moving up with an acceleration of 2.45ms−2. The appar-ent percentage change in his weight is .
A20%B25%C50%D75%A seconds pendulum is suspended form the roof of a lift. If the lift is moving up with an acceleration 9.8m/s2, its time period is
A1sB√2C1√2sD2√2s
The mass of a lift if 600kg and it is moving upwards with a uniform acceleration of 2m/s2. Then the tension in the cable of the lift is :
View SolutionThe mass of a lift is 600 kg and it is moving upwards with a uniform acceleration of 2m/s2. Then the tension in the cable of the lift is-
View SolutionMass of a person sitting in a lift is 50 kg . If lift is coming down with a constant acceleration of 10 m/sec2 . Then the reading of spring balance will be (g=10m/sec2)
View SolutionWhen a lift is moving up with a uniform speed of 1 m/s. the weight of a man recorded bby a weighing machine in the lift is 70 kg . If the lift starts moving down with a uniform speed of 2 m/s, the weight of the man recorded by the weighing machine will be
View SolutionA coin is released inside a lift at a height of 2m from the floor of the lift. The height of the lift is 10 m. The lift is moving with an acceleration of 9m/s2downwards. The time after which the coin will strike with the lift is : (g=10m/s2)
View Solution

