The figure shows mass m moves with velocity u. Find the velocity of ring at that moment. Ring is restricted to move on smooth rod.
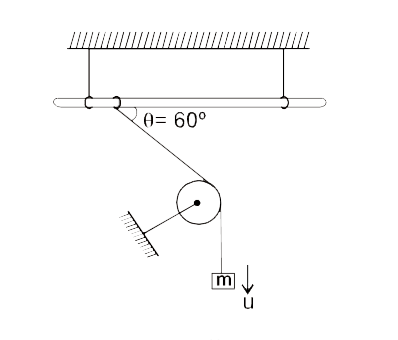
The correct Answer is:VR=ucosθ, VR=2u
Velocity along string remains same .
VRcosθ=u
VR=ucosθ
θ=60∘
VR=2u
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION & FRICTION BOOK - MOTIONCHAPTER - NEWTON'S LAWS OF MOTION & FRICTION EXERCISE - Questions For Practice
25 Videos
- NEWTON'S LAWS OF MOTION & FRICTION BOOK - MOTIONCHAPTER - NEWTON'S LAWS OF MOTION & FRICTION EXERCISE - Exercise - 1 (SECTION-A:- String Constrained, Wedge Constrained, Newtons Law theory Question, Equillibrium Questions (Normal and Tension), Problems with Acceleration (F=ma), Wedge problems)
27 Videos
- NEWTON'S LAWS OF MOTION & FRICTION BOOK - MOTIONCHAPTER - NEWTON'S LAWS OF MOTION & FRICTION EXERCISE - Exercise - 3 Section-B
12 Videos
- MODERN PHYSICS -1BOOK - MOTIONCHAPTER - MODERN PHYSICS -1EXERCISE - EXERCISE-4 ( LEVEL- II)
39 Videos
- NLM & FRICTIONBOOK - MOTIONCHAPTER - NLM & FRICTIONEXERCISE - EXERCISE-4 ( LEVEL-II)
15 Videos
Similar Questions
Find velocity of ring when spring becomes horizontal

View SolutionA charge +Q is uniformluy distributed over a thin ring with radus R.a negative point charge -Q and mass m starts from rest at a pont far away from the centre of the ring and moves towardsn then centre. Find the velocity of this particle at the moment it passes through the centre of the ring .
View Solution
Knowledge Check
A bullet of mass 'm' is fired from a gum of mass M with a (muzzle) velocity u. If the cart on which gun is fixed can move on the smooth horizontal floor as shown

Find recoil velocity of the cartAMucosθM+mBmucosθMCMucosθmDmucosθM+mA bullet of mass 'm' is fired from a gum of mass M with a (muzzle) velocity u. If the cart on which gun is fixed can move on the smooth horizontal floor as shown

Find maximum compression of spring of spring constant (K) isA√MK(mucosθm)B√KM(MucosθM+m)C√MK(mucosθM+m)D√MK(mucosθM)Two small rings, each of mass 'm', are connected to the block of same mass 'm' through an inextensible massless string of length 'l'. Rings are constrained to move over smooth rod AB. Initially, the system is held at rest as shown in Fig. Let a and v be the velocities of ring and block, respectively when string makes an angle 60∘ with the vertical.
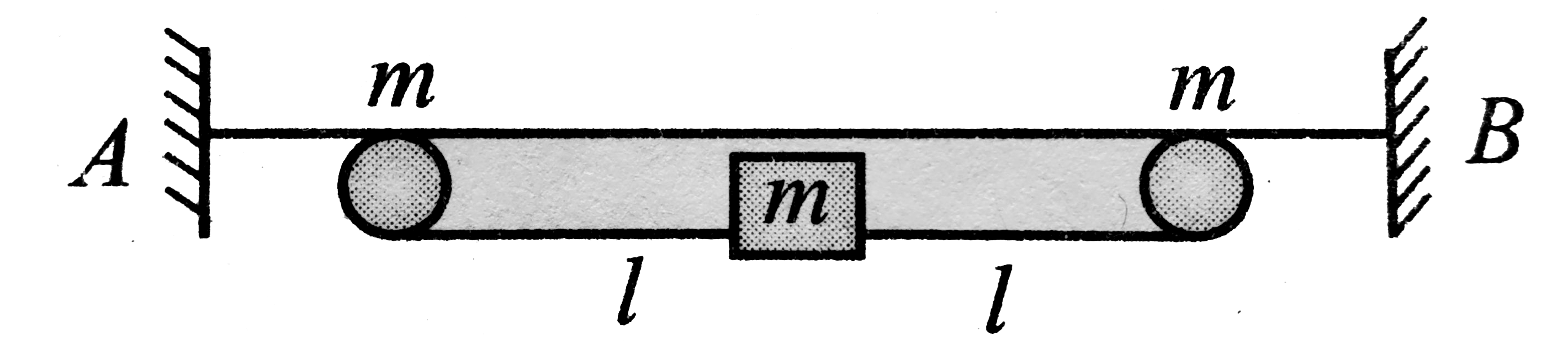 Au=√gl5Bu=√8gl5Cv=√3glDv=√3gl5
Au=√gl5Bu=√8gl5Cv=√3glDv=√3gl5
 ltbgt Find the velocity of block B when ring A is moving downward with velocity v.
ltbgt Find the velocity of block B when ring A is moving downward with velocity v.
View SolutionA rocket moves in the absence of external forces by ejecting a steady jet with velocity u constant relative to the rocket. Find the velocity v of the rocket at the moment when its mass is equal to m, if at the initial moment it possessed the mass m0 and its velocity was equal to zero. Make use of the formula given in the foregoing problem.
View SolutionA smooth rod of length l rotates freely in a horizontal plane with the angular velocity about a stationary vertical axis O as shown in Fig. The moment of inertia of the rod is equal to I relative to the axis. A small ring of mass m is located on the rod close to the rotation axis and is tied to it by a thread. When the thread is burned, the ring starts sliding radially outwards along the rod. Find the velocity v of the ring relative to the rod as a function of its distance r from the rotation axis.
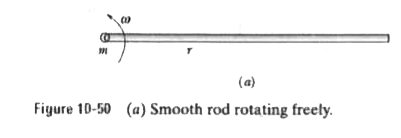
View SolutionA rigid horizontal smooth rod AB of mass 0.75kg and length 40cm can roate freely about a fixed vertical axis through its mid point O. Two rings each of mass 1kg are initially at rest at a distance of 10cm from O on either side of the rod. The rod is set in rotatiob with an angular velocity of 30 radians per second. Find the velocity of each ring along the length of the rod in m/s when they reach the ends of the rod.
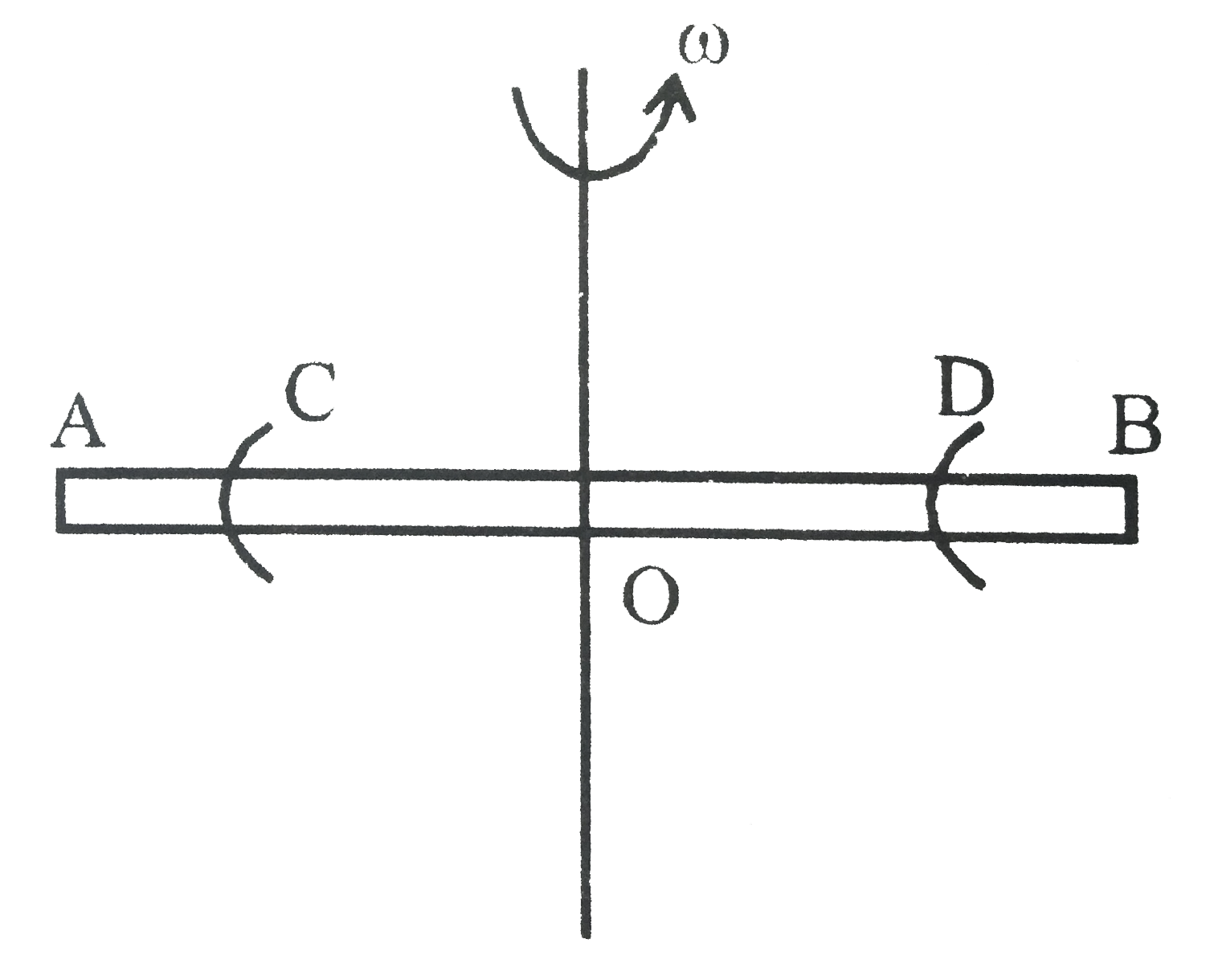 .
.
View SolutionA ball of mass '2m' moving with velocity uˆi collides with another ball of mass 'm' moving with velocity −2uˆi. After the collision, mass 2m moves with velocity u2(ˆi−ˆj). Then the change in kinetic energy of the system ( both balls ) is
View Solution
