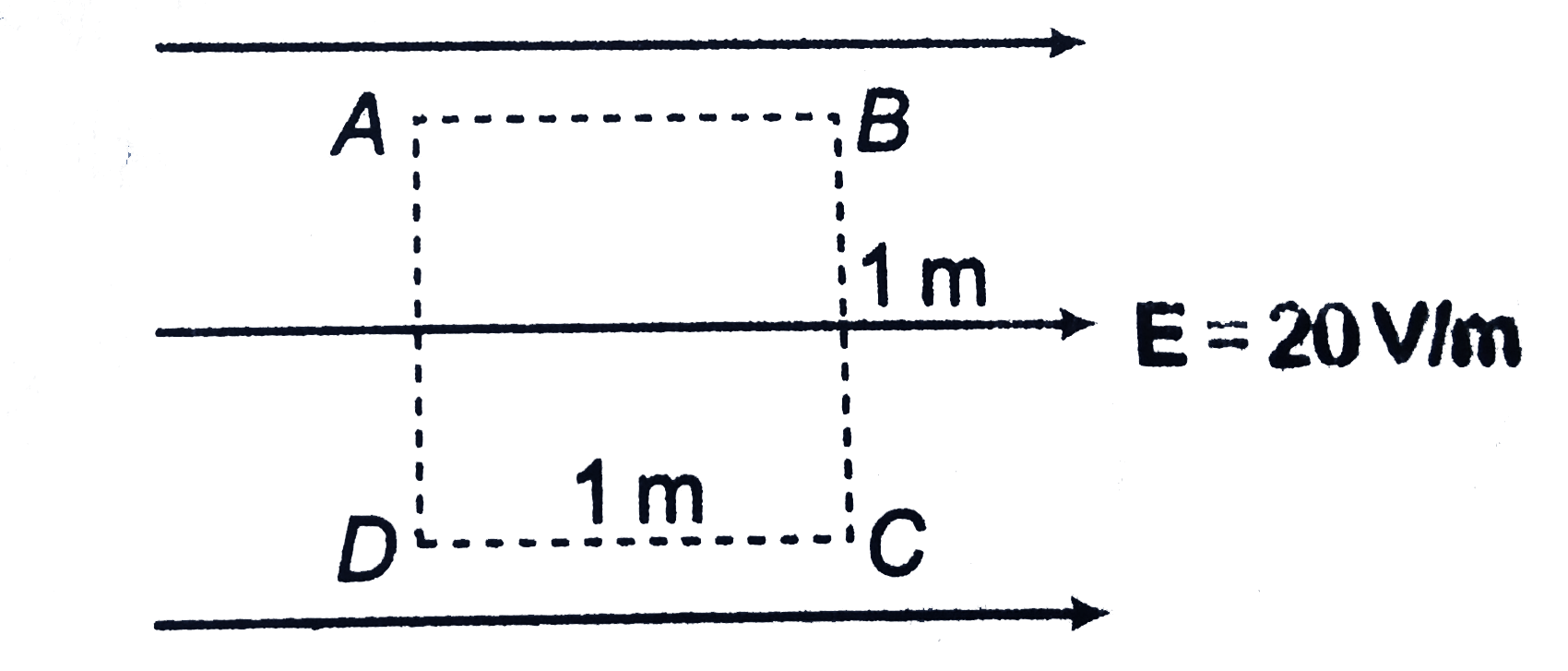
Find out following

(i) VA−VB (ii) VB−VC (iii) VC−VA (iv) VD−VC
(v) VA−VD (vi) Arrange the order of potential for points A, B, C and D.
(i) |ΔVAB|=Ed=20×2×10−2=0.4
so, VA−VB=0.4V
because In the direction of electric field potential always decreases.
(ii) |ΔVBC|=Ed=20×2×10−2=0.4
so, VB−VC=0.4V
(iii) |ΔVCA|=Ed=20×4×10−2=0.8 so, VC−VA=−0.8A
because In the direction of electric field potential always decreases.
(iv) |ΔVDC|=Ed=20×0=0 so, VD−VC=0
because the effective distance between D and C is zero.
(v) |ΔVAD|=Ed=20×4×10−2=0.8, so, VA−VD=0.8V
because In the direction of electric field potential always decreases.
(vi) The order of potential VA>VB>VC=VD.
Topper's Solved these Questions
- ELECTROSTATICSBook:MOTIONChapter:ELECTROSTATICSExercise:SELF MISCELLANEOUS PROBLEM (Example )
Explore 15 Videos
- ELECTROSTATICSBook:MOTIONChapter:ELECTROSTATICSExercise:SELF PRACTICE PROBLEM
Explore 27 Videos
- ELECTRONICS - SEMI CONDUCTORBook:MOTIONChapter:ELECTRONICS - SEMI CONDUCTORExercise:EXERCISE - 3
Explore 29 Videos
- ELECTROSTATICS - I Book:MOTIONChapter:ELECTROSTATICS - I Exercise:EXERCISE - 4 (Level -II) PREVIOUS YEAR - JEE ADVANCED
Explore 13 Videos
Similar Questions
Knowledge Check
Two capacitors C1 and C2 in a circuite are joined as shown. If VA=V1,VB=V2, the potemntial of point P is
 A12(V1−V2)BC2V1+C1V2C1+C2CC1V1+C2V2C1+C2DC2V1−C1V2C1+C2
A12(V1−V2)BC2V1+C1V2C1+C2CC1V1+C2V2C1+C2DC2V1−C1V2C1+C2When perssure is increase at constant temperature, volume of gas decreases, AB → gases,Bc → vapour + liquid ,CD →liquid critical point .At this all the physical properties of liquid phase as density of liquid = density if vapour.
Te or critical temp : Temperature above which a gas can not be liquified
Ve or critical volume : Volume occupied by one mole of gas at Te abd Pe.
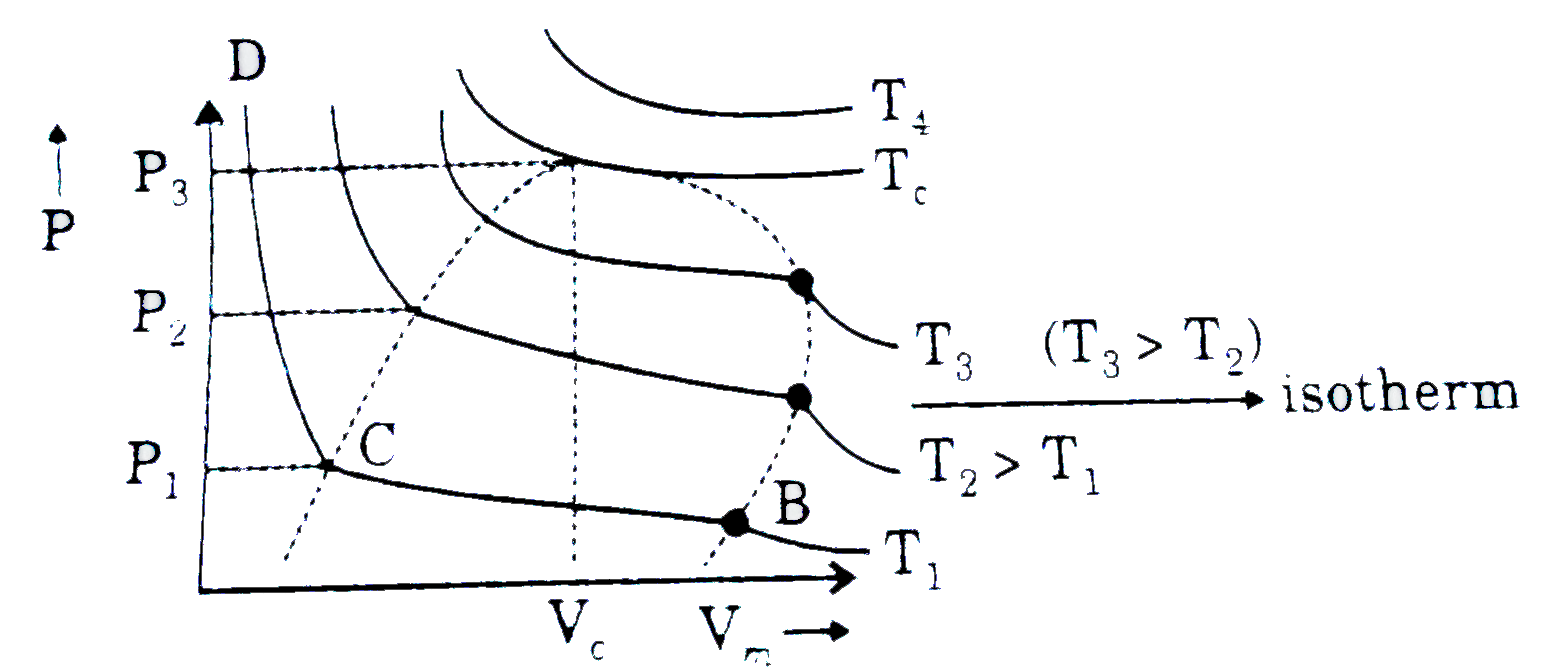
Critical constant Using van der Waals' Equations
(P+aV2m)(Vm−b)=RT
⇒(PV2m+a)(Vm−b)=RTV2m
PV3m+aVm−PbV2m=ab−RTV2m=0
⇒V3m−V2m(b+RTeP)+apVm−abp=0
Since equation is cubic in Vm hence there will be roots of equation at any temperature and pressure.At critical point van der Waals' equation will be
V3m−V2m(b+RTcPc)+apcVm−abpc=0 ....(i)
But at critical point all three roots of the equation should be equal, hence equation should be :
Vm=Vc
(Vm−Vc)3=0
Vm−3V2mVc+3VmV2c−V3c=0....(ii)
Comparing with equation (i)
b+RTcpc=3Vc ...(iii)
apc=3V2e...(iv)
abpc=V3c....(v)
from eqns.(iv) and (v0, Vc=3b
from eq. (iv) pc=a3V2c substituting pc=a3(3b)2=a27b2
from e.q (iii) RTcpc=3Vc−b=9b−b=8b
⇒Tc=8a27Rb
At critical point, the slope of PV curve (slope of isotherm) will be zero at all other point slpoe will be negative zero is the maximum value of slope
(∂P∂Vm)Tc=0...(iv)
∂∂Vm(∂P∂Vm)Tc=0
[Mathematically such points are known as point of inflection (where first two derivatives becomes zero) Using the two TcPc and Vc can be calculated
If the critical constants for a hypothetical van der Waals' gas are Vc=150cm2mol−1,pc=300K Then the approxomate radius of the molecule is :
(TakeR=112Latmmol−1K−1]A(752πNA)1/3B(758πNA)1/3C(3πNA)1/3D(3256πNA)1/3When perssure is increase at constant temperature, volume of gas decreases, AB → gases,Bc → vapour +liquid ,CD → liquid critical point .At this all the physical properties of liquid phase as density of liquid = density if vapour.
Te or critical temp : Temperature above which a gas can not be liquified
Ve or critical volume : Volume occupied by one mole of gas at Te abd Pe.
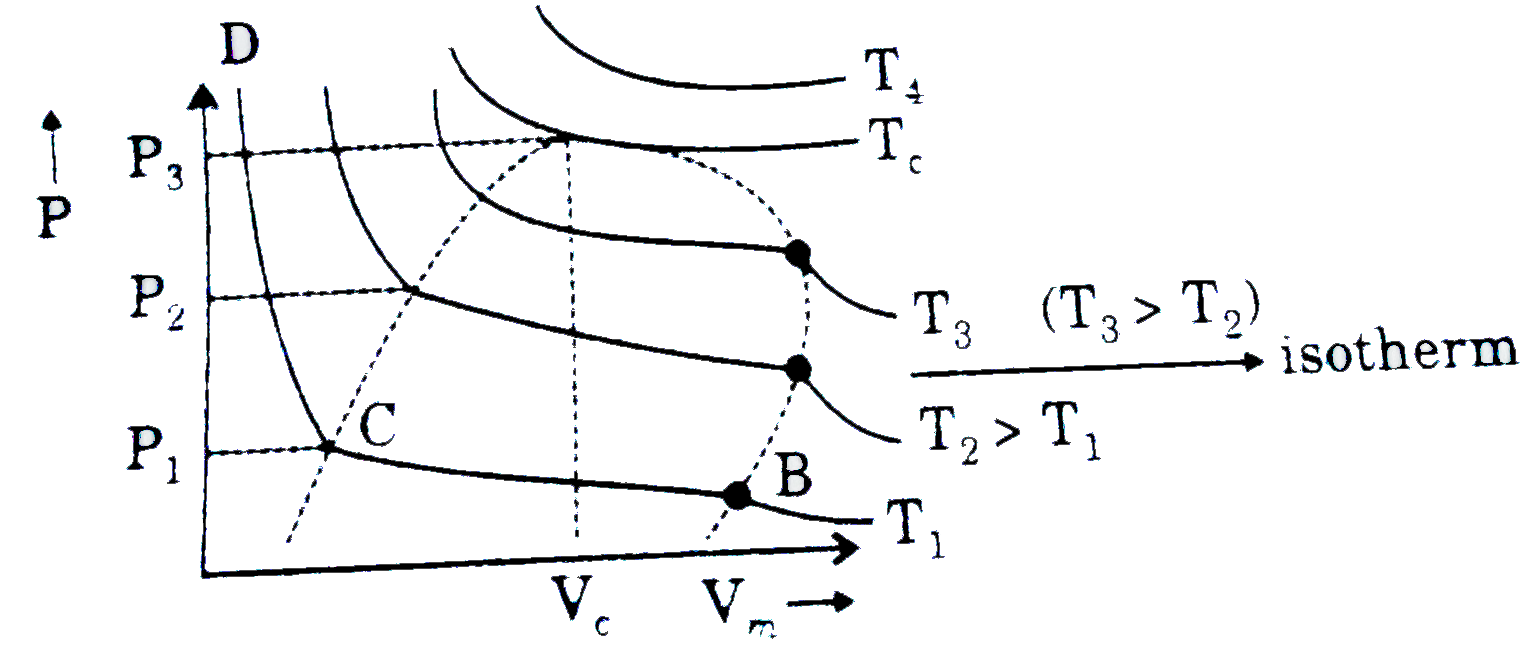
Critical constant Using van der Waals' Equations
(P+aV2m)(Vm−b)=RT
⇒(PV2m+a)(Vm−b)=RTV2m
PV3m+aVm−PbV2m=ab−RTV2m=0
⇒V3m−V2m(b+RTeP)+apVm−abp=0
Since equation is cubic in Vm hence there will be roots of equation at any temperature and pressure.At critical point van der Waals' equation will be
V3m−V2m(b+RTcPc)+apcVm−abpc=0 ....(i)
But at critical point all three roots of the equation should be equal, hence equation should be :
Vm=Vc
(Vm−Vc)3=0
Vm−3V2mVc+3VmV2c−V3c=0....(ii)
Comparing with equation (i)
b+RTcpc=3Vc ...(iii)
apc=3V2e...(iv)
abpc=V3c....(v)
from eqns.(iv) and (v0, Vc=3b
from eq. (iv) pc=a3V2c substituting pc=a3(3b)2=a27b2
from e.q (iii) RTcpc=3Vc−b=9b−b=8b
⇒Tc=8a27Rb
At critical point, the slope of PV curve (slope of isotherm) will be zero at all other point slpoe will be negative zero is the maximum value of slope
(∂P∂Vm)Tc=0...(iv)
∂∂Vm(∂P∂Vm)Tc=0
[Mathematically such points are known as point of inflection (where first two derivatives becomes zero) Using the two TcPc and Vc can be calculated
A scientist proposed the following equation of state
P=RTVm−BV2m+CV2m If this equation leads to the critical behaviour then critical temperature isA8B27RCBB8RCCB23RCDnone of these
Consier the following system & find VC−VA
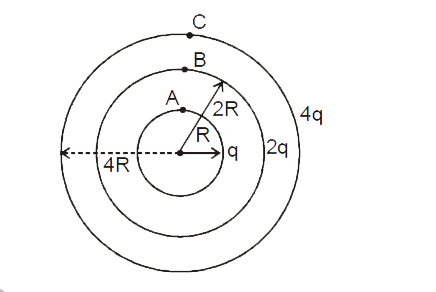
View SolutionWhich of the following is correct for step-up transformer? (A) Vs>Vp (B)Vs<Vp (C) Vs=Vp (D) Vs<<Vp
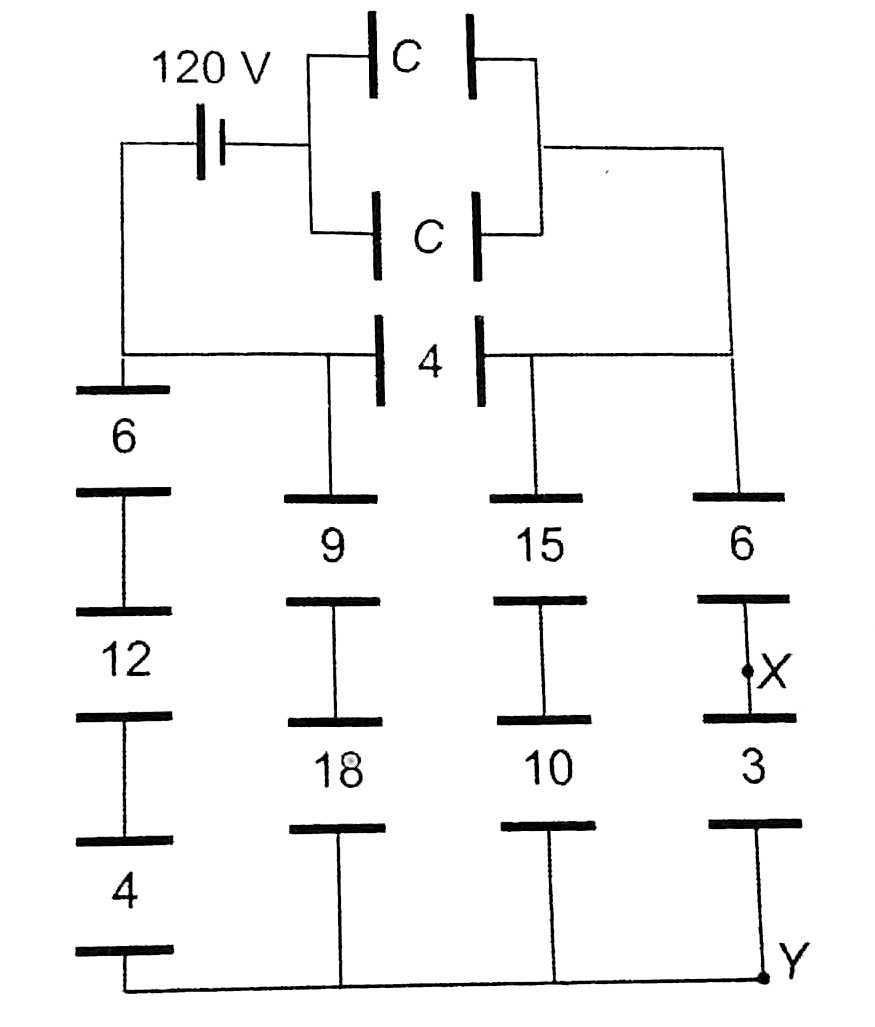
View SolutionIf VX−VY=20V, find the value of C.
View SolutionAt resonance, VL and VC both very much greater than the applied potential, V itself. The quantity factor for an LCR circuit in resonance is given by Q=XLR. In pratice, Q=200 has been achieved.
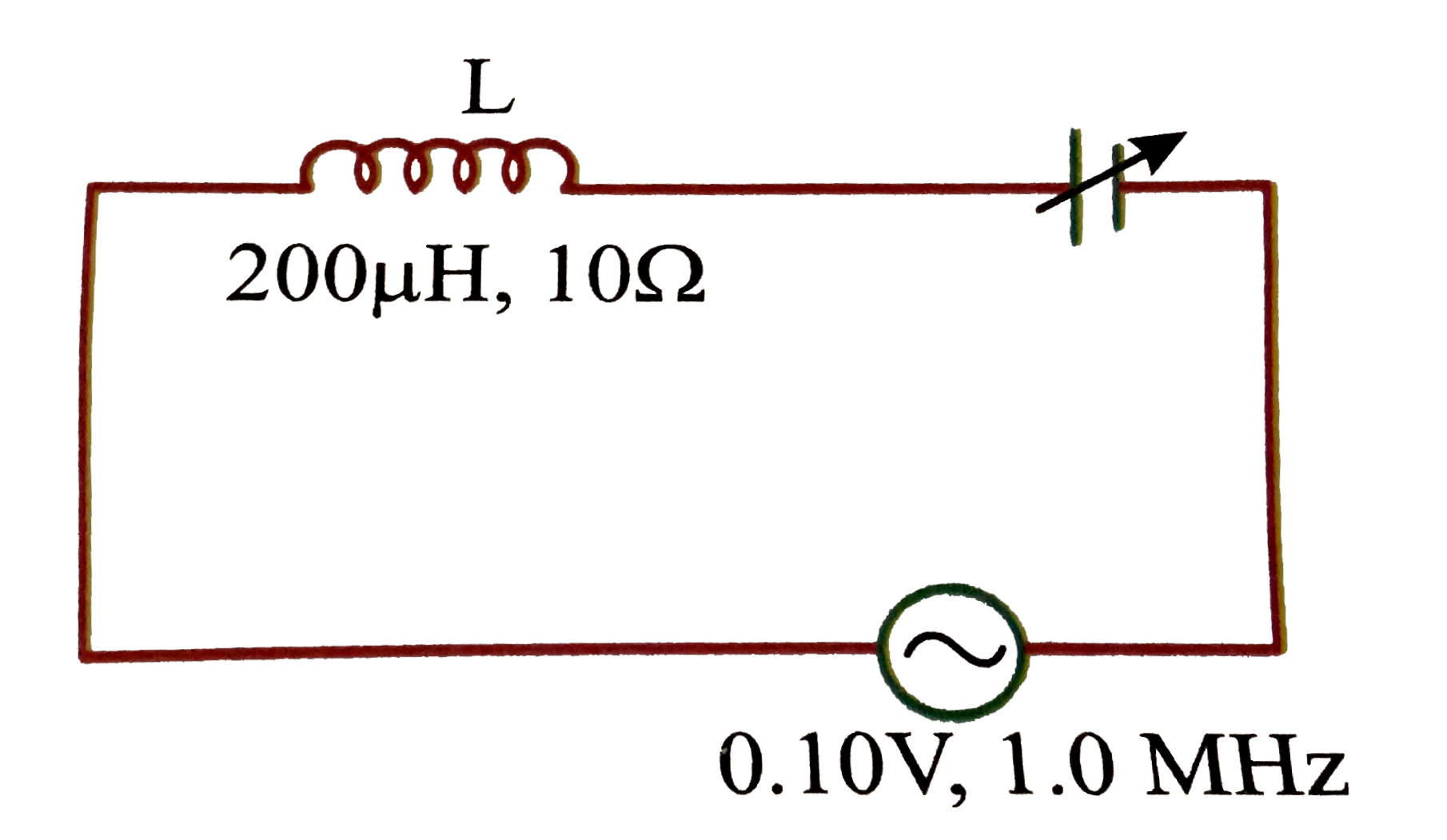
At resonance, the capacitor has been adjusted for
(1). 200×10−6μF
(2) 0.00013μF
(3). 0.0012μF
(4). 0.0013F
At resonance, the potential difference across the inductance is
(1) 1.3V
(2) 13V
(3). 0.3V
(d) none of these
The potential across the capacitor at resosnance is
(1) 1.3V
(2) 13V
(3) <13V
(4) none of these
The Q factor is
(1) VLVC
(2) VCVL
(3) VCV
(d) VLV
(e) choose the right statement.
(1) VL+VC can be greater than Vapplied
(2) VL+VC=Vapplied
(3) VL+VC<Vapplied
(4) none of these
View SolutionIn the uniform electric field shown in figure, find :
a. VA−VD
b. VA−VC
c. VB−VD
d. VC−VD
View Solution

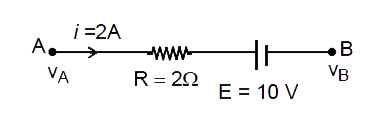
 .
.