Five point charges, each of value +q are placed on five vertices of a regular hexagon of side Lm. What is the magnitude of the force on a point charge of value -q coulomb placed at the centre of the hexagon?
Method : I
If there had been a sixth charge +q at the remaining vertex of hexagon force due to all the six charges on - q at O would be zero (as the forces due to individual charges will balances each other), i.e.,
Now if is the force due to sixth charge and due to remaining five charges.
i.e.
or,
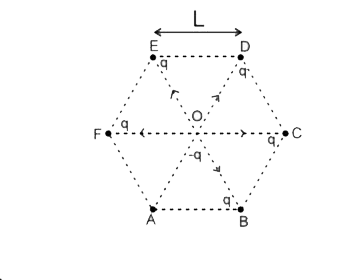
along CO
Method : II
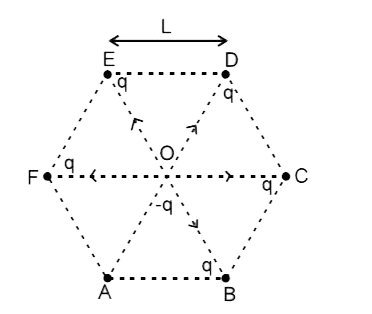
In the diagram we can see that force due to charge A and D are opposite to each other
...(i)
Similarly ...(ii)
So
Using (i) and (ii) along CO.
(A) The total charge of the rod cannot be considered to be placed at the centre of the rod as we do in mechanics for mass in many problems.
(B) If then behaviour of the rod is just like a point charge.
Topper's Solved these Questions
- ELECTROSTATICSBook:MOTIONChapter:ELECTROSTATICSExercise:SELF MISCELLANEOUS PROBLEM (Example )
Explore 15 Videos
- ELECTROSTATICSBook:MOTIONChapter:ELECTROSTATICSExercise:SELF PRACTICE PROBLEM
Explore 27 Videos
- ELECTRONICS - SEMI CONDUCTORBook:MOTIONChapter:ELECTRONICS - SEMI CONDUCTORExercise:EXERCISE - 3
Explore 29 Videos
- ELECTROSTATICS - I Book:MOTIONChapter:ELECTROSTATICS - I Exercise:EXERCISE - 4 (Level -II) PREVIOUS YEAR - JEE ADVANCED
Explore 13 Videos
Similar Questions
Five point charges, each of value +q coul, are placed on five vertices of a regular hexagon of isde L meters. The magnitude of the force on the point charge of value -q coul, placed at the centre of the hexagen is…………….
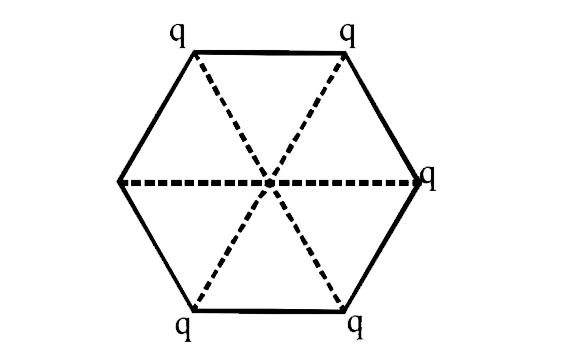
View SolutionFive point charges each of charges +q are placed of five vertices of a regular hexagon of side 'l'. Find the magnitude of the resultant force on a charge -q placed at the centre of the hexagon.
(##U_LIK_SP_PHY_XII_C01_E09_018_Q01.png" width="80%">
View Solution
Knowledge Check
Three point charges each of value +q are placed on three vertices of a square of side a metre. What is the magnitude of the force on a point charge of value −q coulomb placed at the centre of the square?
A(14πε0)(qa)2B(12πε0)(2qa)2C(12πε0)(qa)2D(14πε0)(2qa)2Five point charges each of charge + q are placed on five vertices of a regular of side h as shown in the figure. Then
Athe forces on (-q) at O due to charges +q at A and D are balanced.Bthe forces on (-q) due to charges at D and E are balanced.CThe resultant force on −q at O is 14πε0q2h2 along OE.DThe resultant force on - q at O is 14πε0q2h2 along OC.Five point charge (+q each) are placed at the five vertices of a regular hexagon of side 2a.what is the magnitude of the net electric field at the centre of the hexazon?
A14πε0qa2Bq16πε0a2C√2q4πε0a2D5q16πε0a2
Five point charges, each +q are placed on five vertices of a regular hexagon of side' l '. Find the magnitude of the resultant force on a charge –q placed at the centre of the hexagon.
View SolutionFive equal charges each of value q are placed at the corners of a regular pentagon of side a. The electric field at the centre of the pentagon is

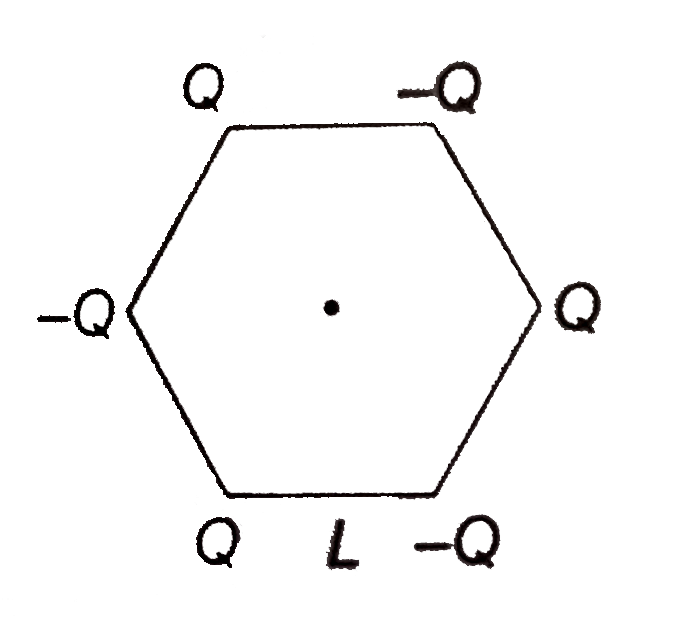
View SolutionThe point charges are placed on the vertices of regular hexagon of side L as shown. Find the potential energy of the system of charges.
View SolutionFive point charge (+q each) are placed at the five vertices of a regular hexagon of side 2a.what is the magnitude of the net electric field at the centre of the hexazon?
View SolutionFive point charges, +q each are placed at the five vertices of a regular hexagon. The distance of the center of the hexagon from any fo the vertices is a. the electric field at the center of the hexagon is
View Solution