Three infinitely long conductors R, S and T are lying in a horizontal plane as shown in the figure. The currents in the respective conductors are
IR=I0sin(ωt+2π3)
IS=I0sin(ωt)
IT=I0sin(ωt−2π3)
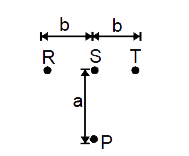
Find the amplitude of the vertical component of the magnetic field at a point P, distance ‘a’ away from the central conductor S.
Video Solution
Text Solution
μ0102π√3b(a2+b2)
|
Topper's Solved these Questions
- MAGNETISM Book:MOTIONChapter:MAGNETISM Exercise:EXERCISE-4 (LEVEL-I)
Explore 33 Videos
- MAGNETISM Book:MOTIONChapter:MAGNETISM Exercise:EXERCISE-4 (LEVEL-II)
Explore 40 Videos
- MAGNETISM Book:MOTIONChapter:MAGNETISM Exercise:EXERCISE-3 (Level-I)
Explore 46 Videos
- LOGIC GATESBook:MOTIONChapter:LOGIC GATESExercise:EXERCISE - 2
Explore 10 Videos
- MAGNETISM -1Book:MOTIONChapter:MAGNETISM -1Exercise:Exercise - 3 SECTION -A
Explore 56 Videos
Similar Questions
Knowledge Check
If i1=i0sin(ωt),i2=i02sin(ωt+ϕ), then i3=
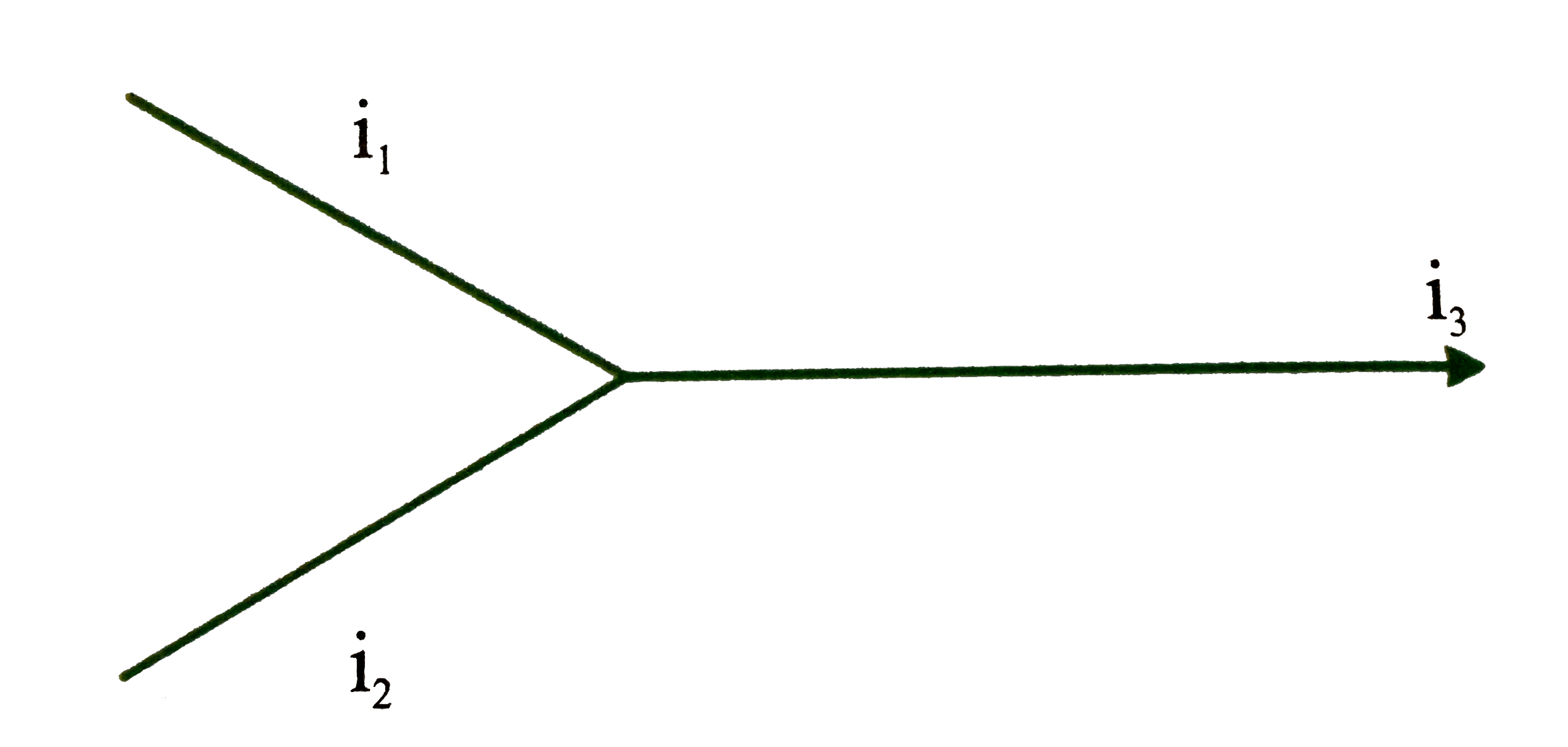 A√i201+i202sin{ϕ+ωt}B(i01+i02)sin(ϕ2+ωt)C(√i201+i202+2i01i02cosϕ)sin[ϕ+ωt]D(√i201+i202+2i01i02cosϕ)sin[α+ωt] where α=Tan−1[i02sinϕi01+i02cosϕ]
A√i201+i202sin{ϕ+ωt}B(i01+i02)sin(ϕ2+ωt)C(√i201+i202+2i01i02cosϕ)sin[ϕ+ωt]D(√i201+i202+2i01i02cosϕ)sin[α+ωt] where α=Tan−1[i02sinϕi01+i02cosϕ]The instantaneous values of emf and the current in a series ac circuit are -
E = Eo Sin ω t and l = lo sin (ωt+π/3) respectively, then it isANecessarily a RL circuitBNecessarily a RC circuitCNecessarily a LCR circuitDCan be RC or LCR circuitTwo parallel S.H.M.s have equations y1=A1sin(ωt+2π) and y2=A2sin(ωt+4π). The amplitude of the resultant motion is
A+=(A1+A2)B+=(A1−A2)C√A21+A22+A1A2D√A21+A22
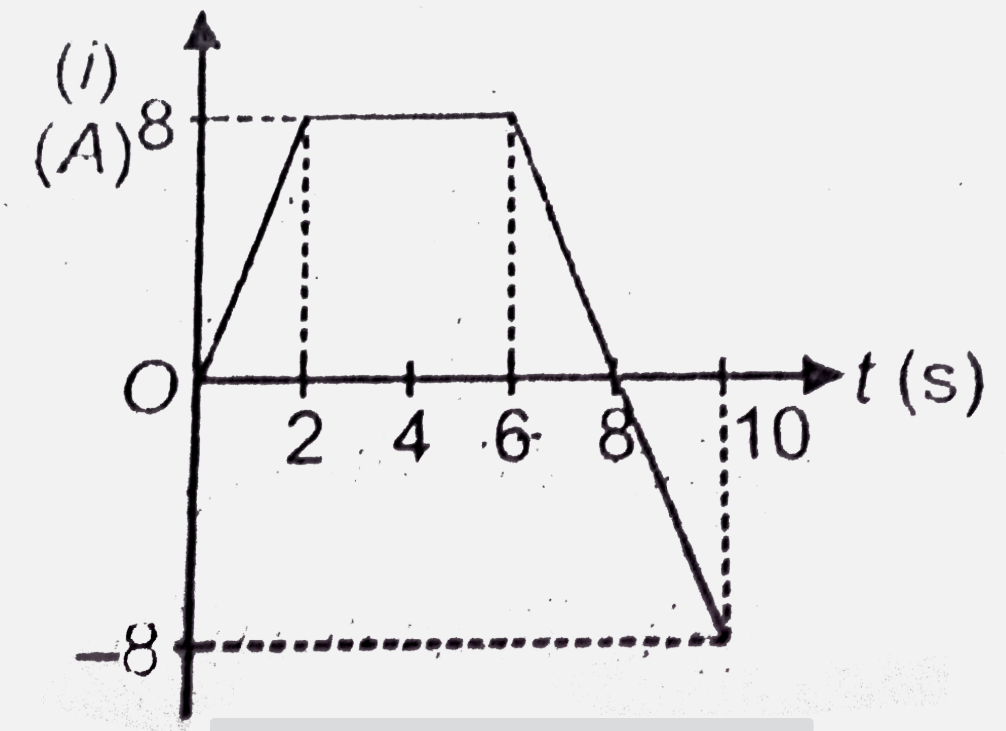
The current I through a conductor varies with time t as shown in figure. The average electric current during t=0 to t=10 s will be
View SolutionWhat is the power dissipation in an AC circuit in which voltage and current are given by V=300sin(ωt+π2) and I = 5 sinωt ?
View SolutionAn AC source producing e.m.f V=V0(sinωt+sin3ωt) is connected in series with a capacitor and a resistor. The current in the circuit is found to be i=i1sin(ωt+ϕ1)+i2sin(3ωt+ϕ2) then comment
View SolutionThe power dissipated in alternating circuit with voltage e=e0 sin ωt and current I=I0sin(ωt−ϕ) is
View SolutionThe magnetic field at a distance r from a long wire carrying current i is 0.4 T. The magnetic field at a distance 2r is
View Solution