A current I flows around a closed path in the horizontal plane of circle as shown in the figure The path consists of eight arcs with alternating radii r and 2r . Each segment of arc subtends equal angle at the common centre P The magnetic field produced by current path at point P is
 .
.
38μ0Ir , perpendicular to the plane of the paper and directed inward
38μ0Ir , perpendicular to the plane of the paper and directed outward
18μ0Ir , perpendicular to the plane of the paper and directed inward
18μ0Ir , perpendicular to the plane of the paper and directed outward
The correct Answer is:A
Step by step video, text & image solution for A current I flows around a closed path in the horizontal plane of circle as shown in the figure The path consists of eight arcs with alternating radii r and 2r . Each segment of arc subtends equal angle at the common centre P The magnetic field produced by current path at point P is . by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MAGNETISM BOOK - MOTIONCHAPTER - MAGNETISM EXERCISE - EXERCISE-2 (Level-I)
40 Videos
- MAGNETISM BOOK - MOTIONCHAPTER - MAGNETISM EXERCISE - EXERCISE-2 (Level-II)
15 Videos
- MAGNETISM BOOK - MOTIONCHAPTER - MAGNETISM EXERCISE - EXERCISE-4 (LEVEL-II)
40 Videos
- LOGIC GATESBOOK - MOTIONCHAPTER - LOGIC GATESEXERCISE - EXERCISE - 2
10 Videos
- MAGNETISM -1BOOK - MOTIONCHAPTER - MAGNETISM -1EXERCISE - Exercise - 3 SECTION -A
56 Videos
Similar Questions
A current of 10A flows around a closed path in a circuit which is int eh horizontal plne as shown in the figure. The circuit consists oif eight alternating arcs of radii r1=0.08m and r2=0.12m. Each subtends the same angle at the centre.
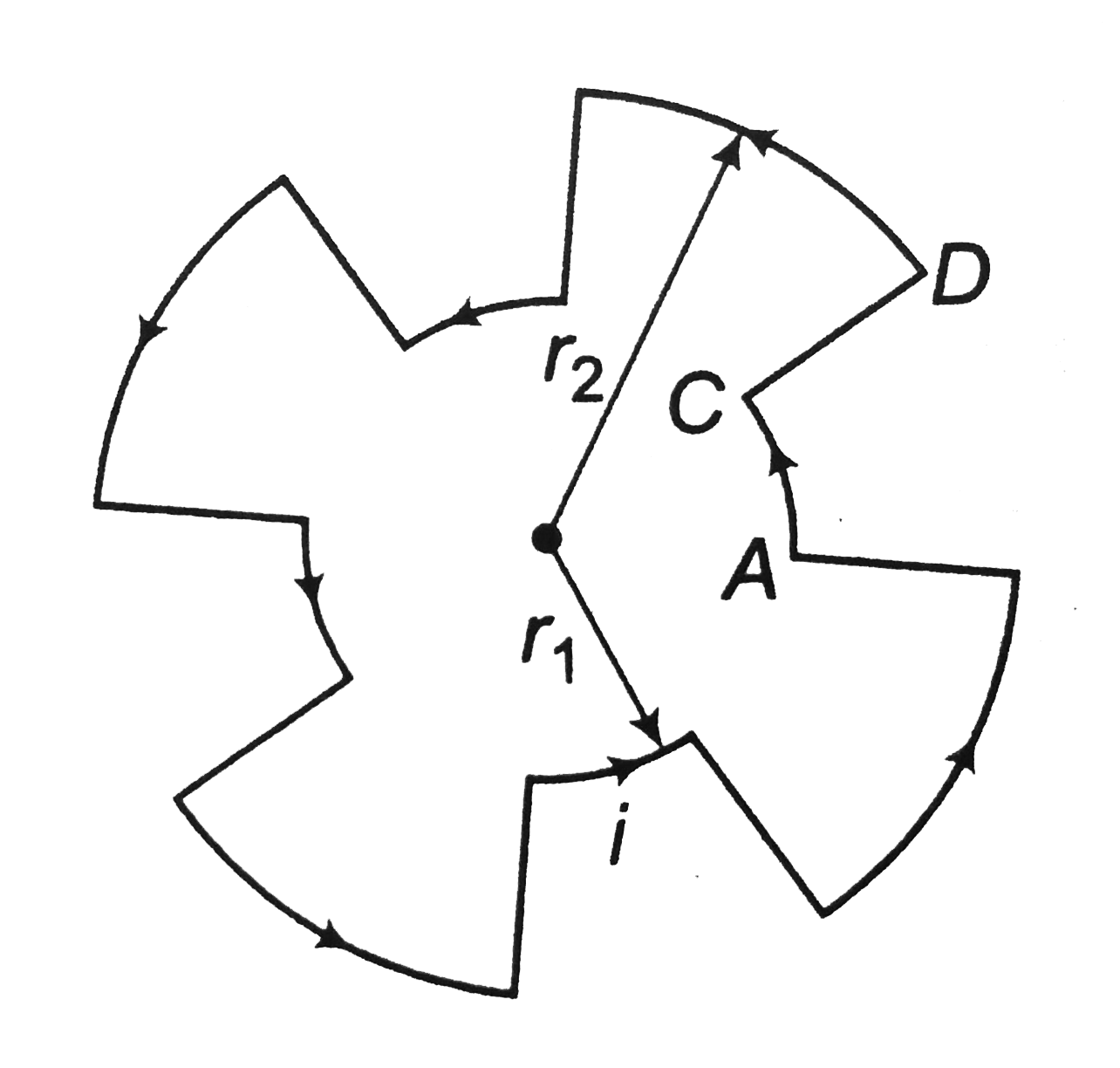
a. Find the magnetic field produced by this circuit at the centre.
b. An infinitely long straight wire carryin as current of 10A is passing through the centre of the above circuit vertically with the direction of the current being into the pane of the circuit. what is the force acting on the wire at the centredue to the curren in the circuit? What is the force acting on the arc AC and the straight segment CD due to the current at the centre?
View SolutionA current of 10A flows around a closed path in a circuit which is in horizontal plane as shown in the figure . The circuit consists of eight alternating arcs of radiir1=0.08mandr1=0.12m.Eacharc⊂tendsthesameathecenter.<br>(a)F∈dthemag≠tixcfield∏ucedbythis∘uitatthecenter.<br>(b)An∈f∈itelylongstraightwirecarry∈gacurrentof10 Aispassingthroughthecenteroftheabove∘uitverticallywiththedirectionofthecurrentbe∈g∫othepla≠ofthe∘uit.Wˆistheforceact∈gonthearcACandthestraightsegment CD due to the current at the center?
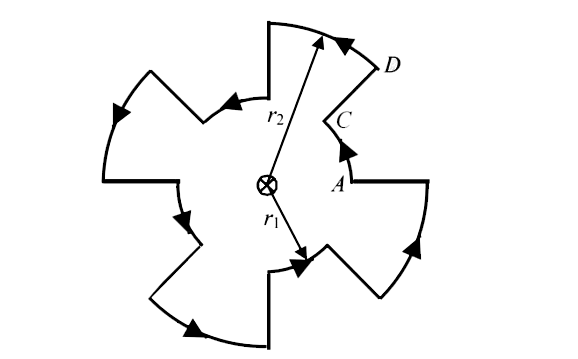
View Solution
Knowledge Check
A current I flows through a closed loop as shown in figure. The magnetic field induction at the centre 0 is
 Aμ0I4πRθBμ0I4πR(θ+sinθ)Cμ0I4πR(π−θ+sinθ)Dμ0I4πR(π−θ+tanθ)
Aμ0I4πRθBμ0I4πR(θ+sinθ)Cμ0I4πR(π−θ+sinθ)Dμ0I4πR(π−θ+tanθ)An arc of a circle of radius R subtends an angle π2 at the centre. It carriers a current i. The magnetic field at the centre will be
Aμ0i2RBμ0i8RCμ0i4RD2μ0i5RAn are of a circle of a radius R subtends an angle π2 at the centre .it carries a current l. The magnetic field at the centre will be
Aμ0I2RBμ0I8RCμ0I4RDμ0I5R
Calculate the magnetic field at point O for the current-carrying wire segment shown in Fig. The wire consists of two straight portions and a circular arc of radius a, which subtends an angle θ.
View SolutionThe segment of wire shown in figure carries a current of i=5 A. The magnetic field (in Tesla) at the point P is

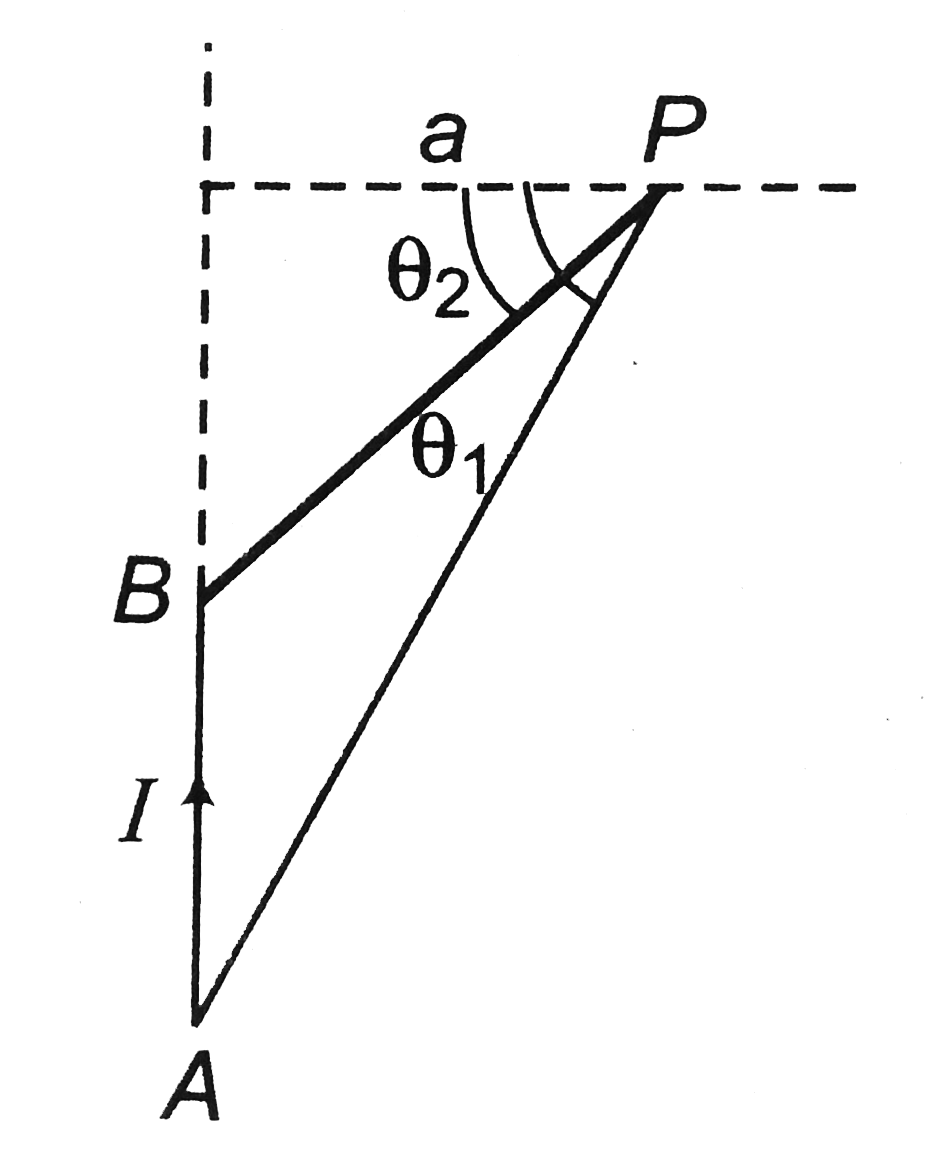
View SolutionThe straight wire AB carries a current I. The ends of the wire subtend angles θ1 and θ2 at the point P as shown in figure. The magnetic field at the point P is
View SolutionA current I ampere flows in the loop having circular arc of radius r metre subtending an angle 6 as shown in figure. The magnetic field, at center of circle is
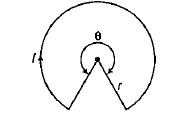
View SolutionA current i ampere flows in the loop having circular arc of radius r metre subtending an angle θ∘as shown in figure. The magnetic field at centre O of circle is
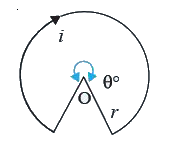
View Solution
