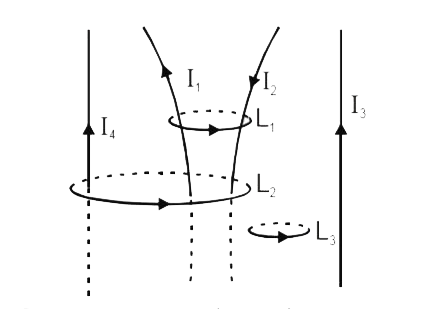
Find the values of ∮→B.→dl for the loops L1,L2andL3 in Fig. (The sense of →dl is mentioned in the figure)

for L1∮→B.→dl=μ0(I1−I2)
here I1 is taken positive because magnetic lines of force produced by I1 is anti clockwise as seen from top. I2 produces lines of →B in clockwise sense as seen from top. The sense of →dl is anticlockwise as seen from top. for L2:∮→B.→dl=μ0(I1−I2+I4)
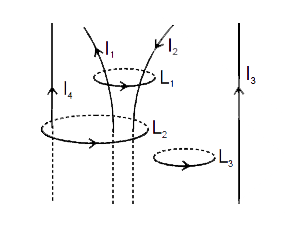
for L3:∮→B.→dl=0
Topper's Solved these Questions
- MAGNETISM BOOK - MOTIONCHAPTER - MAGNETISM EXERCISE - EXERCISE-1
50 Videos
- MAGNETISM BOOK - MOTIONCHAPTER - MAGNETISM EXERCISE - EXERCISE-2 (Level-I)
40 Videos
- LOGIC GATESBOOK - MOTIONCHAPTER - LOGIC GATESEXERCISE - EXERCISE - 2
10 Videos
- MAGNETISM -1BOOK - MOTIONCHAPTER - MAGNETISM -1EXERCISE - Exercise - 3 SECTION -A
56 Videos
Similar Questions
Knowledge Check
Rank the value of ∮→B→dl for the closed paths shown in figure from the smallest to largest.
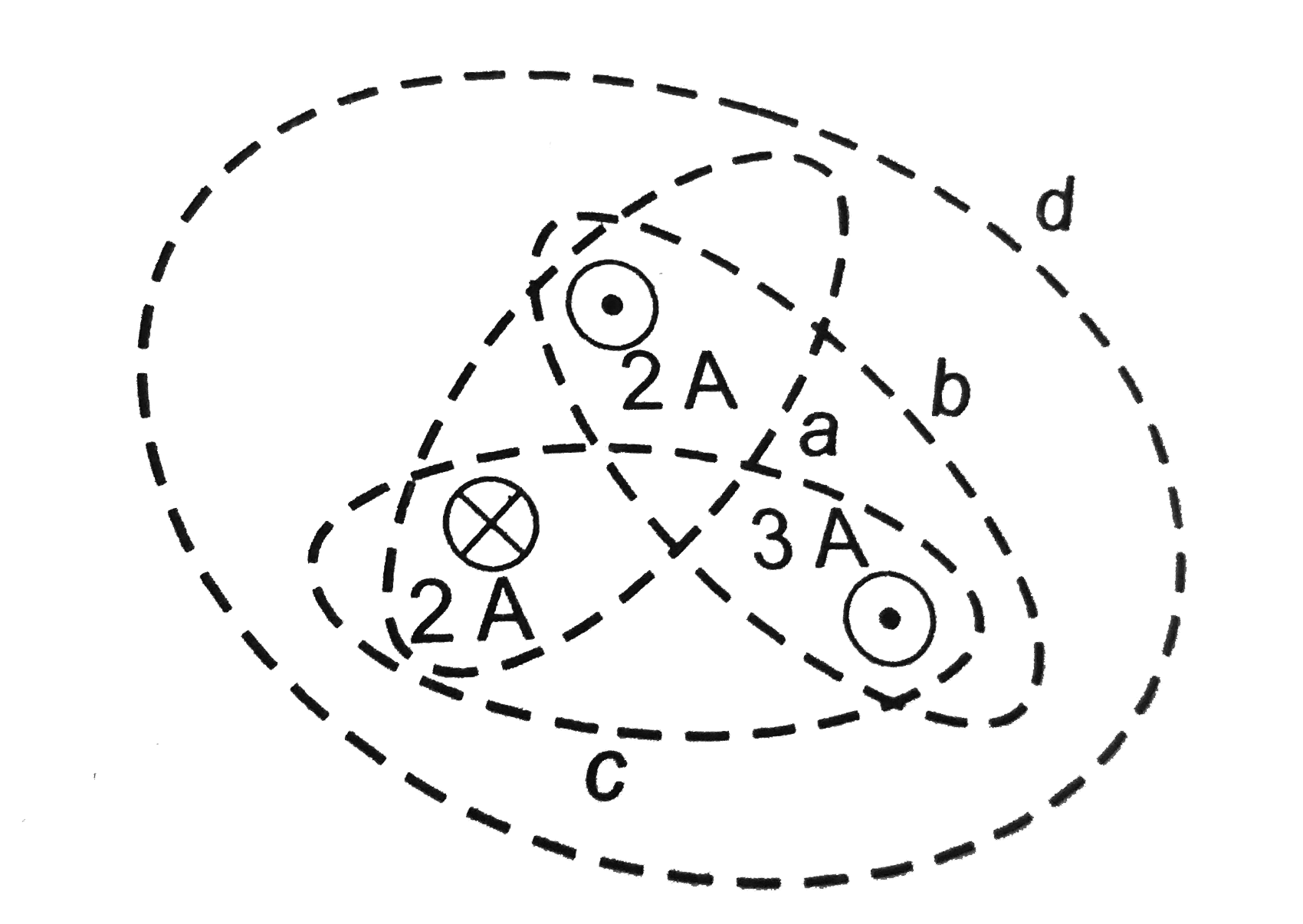 Aa,b,c,dBa,c,d,BCa,d,c,bDa,c,b,d
Aa,b,c,dBa,c,d,BCa,d,c,bDa,c,b,dCurrent I0 is flowing through a bent wire a→b→c→d in z−x plane as shown in figure, then ∮→B.→dl over the loop PQRS lying in the X-Y plane as shown in figure, due to the bent wire abcd
 Aμ0I08Bμ0I07Cμ0I05Dμ0I03
Aμ0I08Bμ0I07Cμ0I05Dμ0I03In the circuit shown in Fig. If both the lamps L1 and L2 are identical.
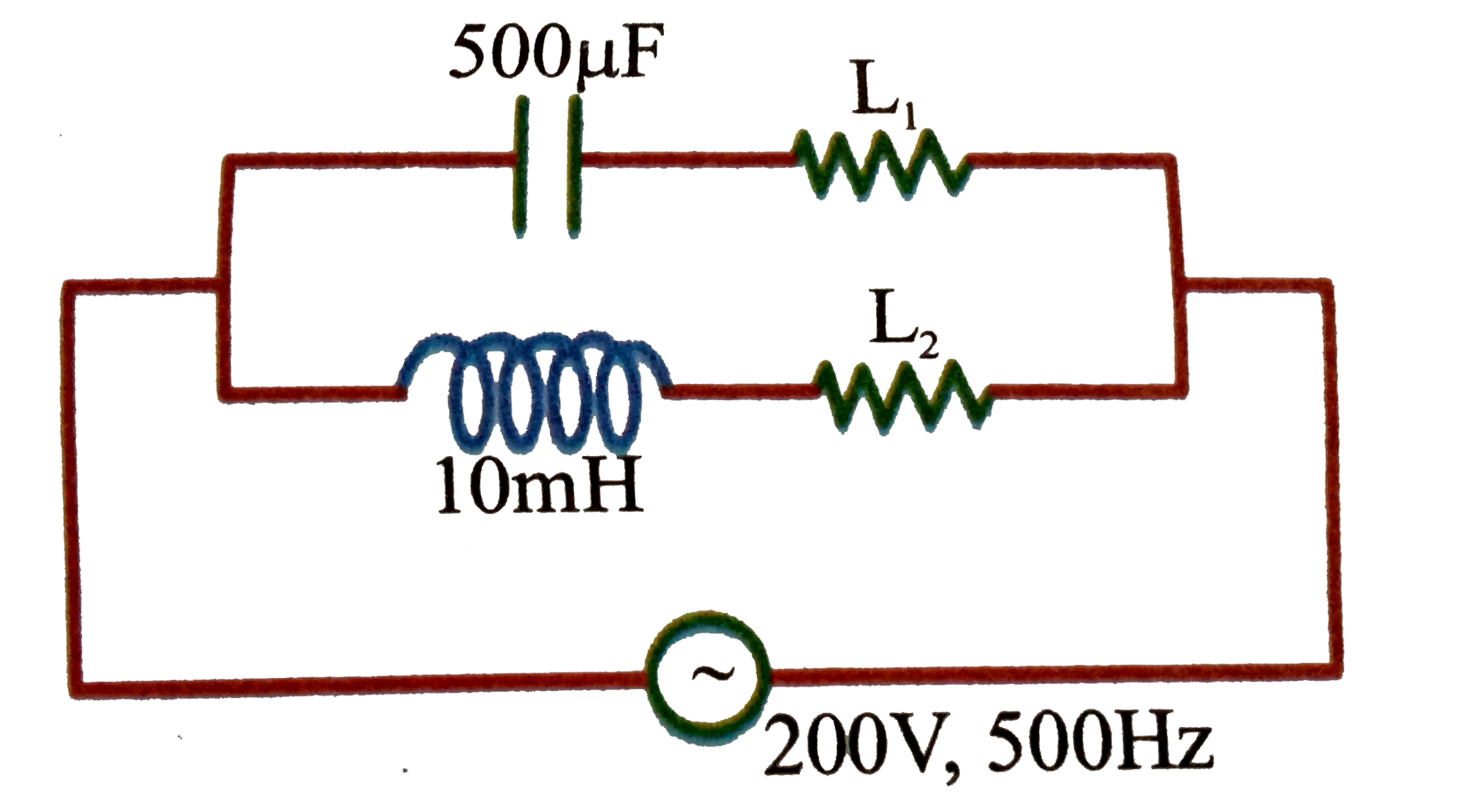 Atheir brightness will be sameBL1 will be brighter than L2CAs the frequency of supply voltage in increased, brightness of L1 will increase and that of L1 will decreaseDOnly L2 will glow because the capacitor has infinite resistance
Atheir brightness will be sameBL1 will be brighter than L2CAs the frequency of supply voltage in increased, brightness of L1 will increase and that of L1 will decreaseDOnly L2 will glow because the capacitor has infinite resistance
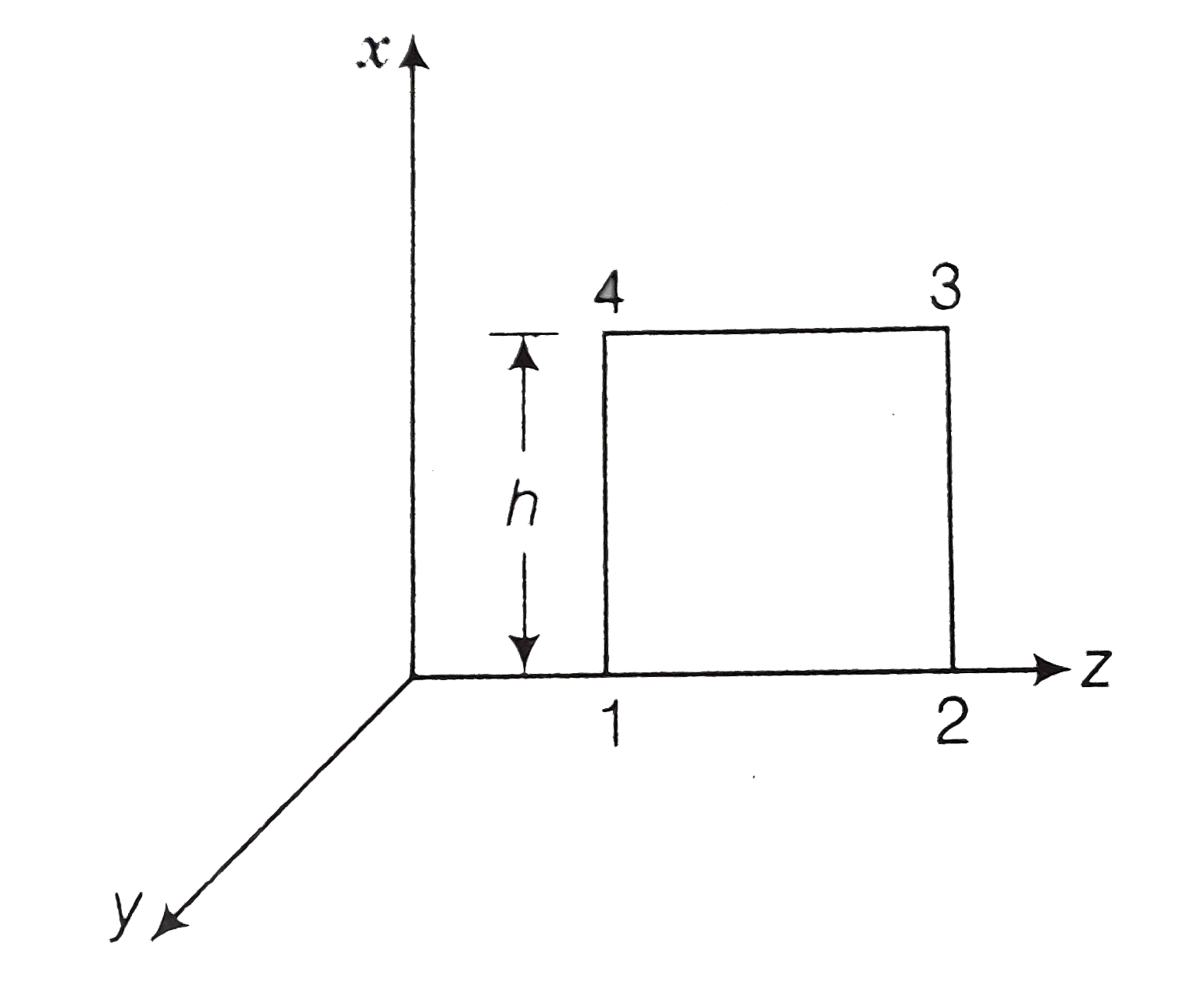
A plane EM wave travelling in vacuum along z-direction is given by E=E0 sin (kz−ωt)ˆi and B=B0 sin (kz−ωt)ˆj
(i) Evaluate ∫E.dl over the rectangular loop 1234 shown in figure.
(ii) Evaluate ∫B.ds over the surface bounded by loop 1234.
(iii) Use equation ∫E.dl=−dϕBdt to prove E0B0=c.
(iv) By using similar proces and the equation
∫B.dl=μ0I+ε0dϕEdt, prove that c1√μ0ε0
View SolutionA closed curve encircles several conductors. The line integral ∮→B.→dl around this curve is 3.83×10−4Tm.
(a) What is the net current in the conductor?
(b) If you were to integrated around the curve in the opposite direction, what would be the value of the line integral? Expalin.
View SolutionFind ∮→B.→dl over following loops (direction in which integration has to be performed is indicated by arrows)

View SolutionA: In any magnetic field region the line integral ∮→B.→dl along a closed loop is always zero.
R: The magnetic field →B in the expressioin ∮→B.→dl is due to the currents enclosed only by the loop.
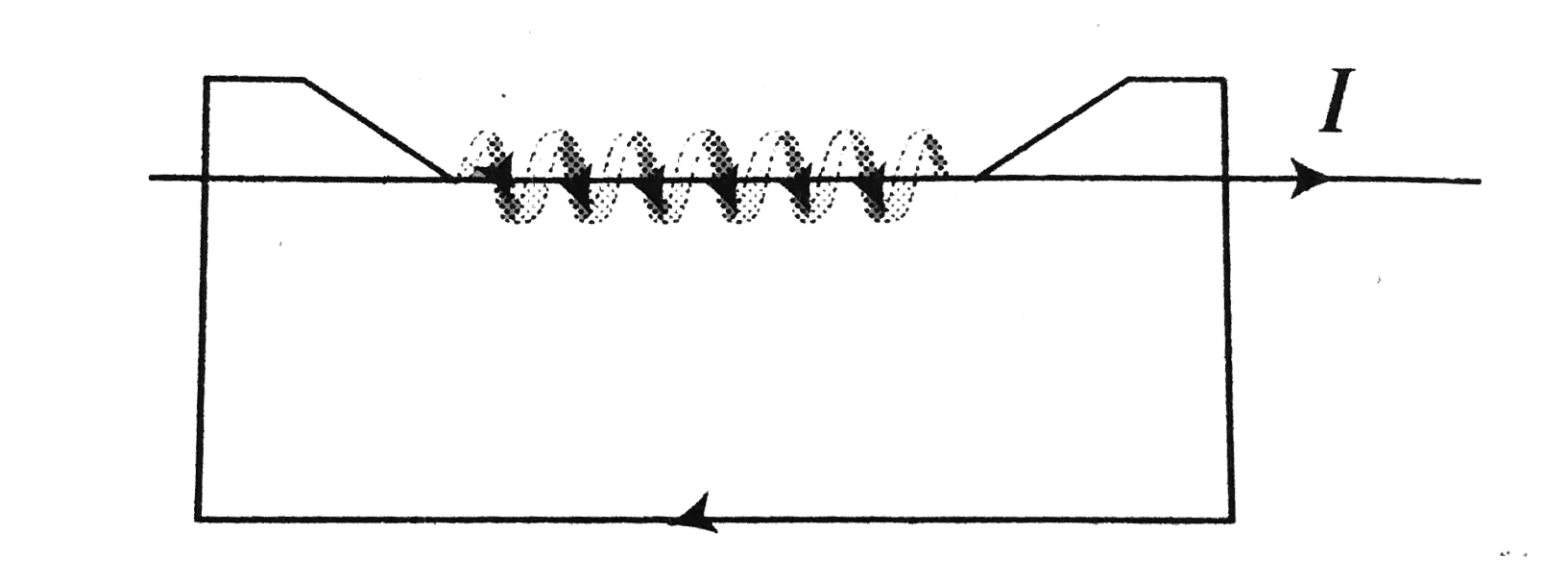
View SolutionIn the diagram shown, a wire carriers current I. The loop has N turns and part of helical loop on which arrows are drawn is outside the plane of paper. What is the value of the ∮→B.→dl (as in Ampere's law) on the helical loop shown in the figure?
View Solution