For a prism, $A = 60^{\circ}, n = \sqrt{7 / 3}$ . Find the minimum possible angle of incidence, so that the light ray is refracted from the second surface. Also, find $δ_{max}$ .

Video Solution

Text Solution

Verified by Experts

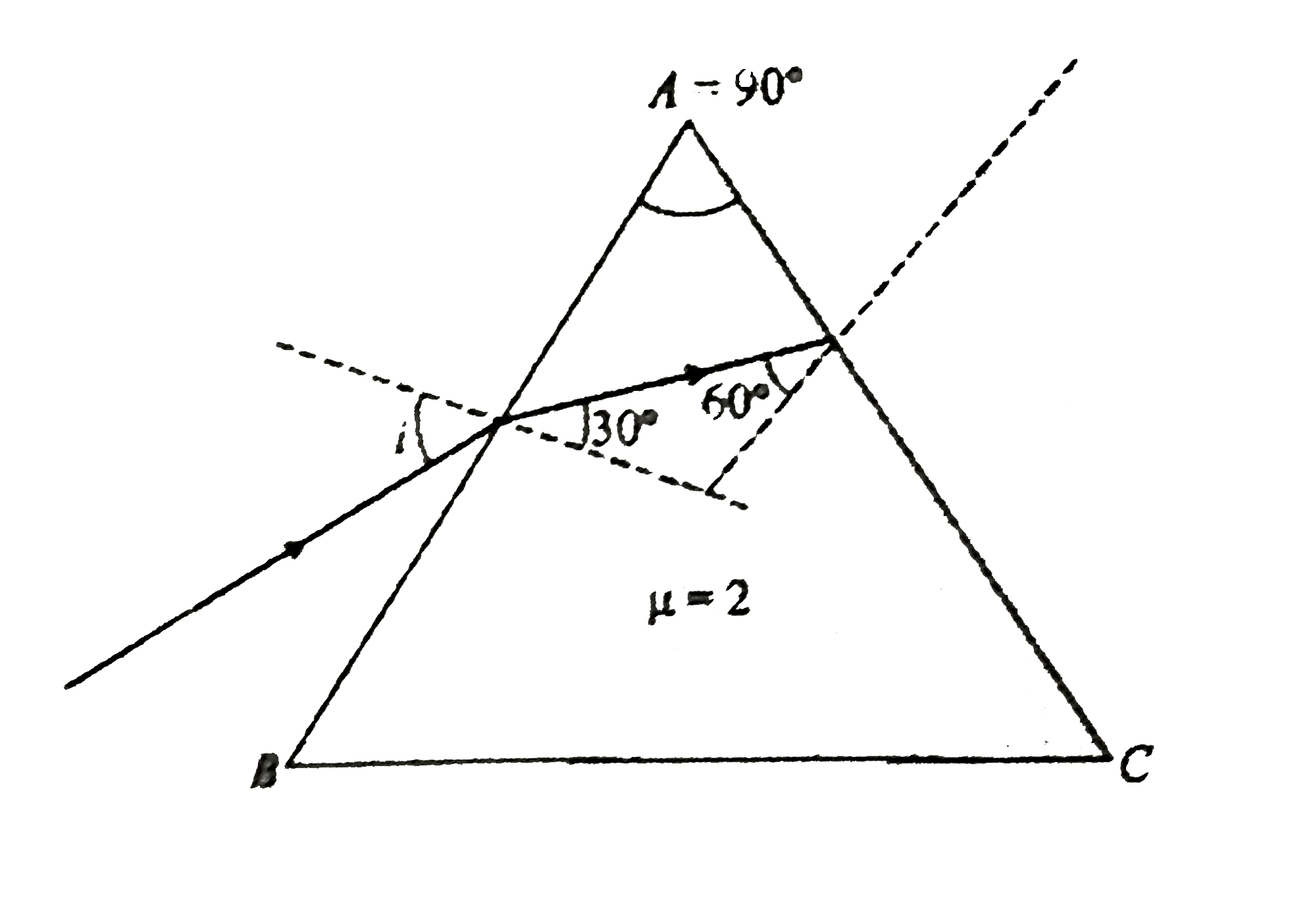
In minimum incidence case the angles will be as shown in figure
Applying snell’s law :
$1 \times {sin i}_{sin} = \sqrt{\frac{7}{3}} sin (A - C)$
$= \sqrt{\frac{7}{3}} (sin A cos C - cos A sin C)$

$= \sqrt{\frac{7}{3}} (sin 60 \sqrt{1 - \frac{3}{7}} - cos 60 \sqrt{\frac{3}{7}}) = \frac{1}{2}$
$∴ i_{min} = 30^{\circ}$
$∴ δ_{max} = i_{min} + 90^{\circ} - A$
$= 30^{\circ} + 90^{\circ} - 60^{\circ} = 60^{\circ}$

Updated on:21/07/2023

Light ray is incident on a prism of angle $A = 60^{\circ}$ are refractive index $μ = \sqrt{2}$ . The angle of incidence which the emergent rays grazes the surface is given
A ${sin}^{- 1} (\frac{\sqrt{3} - 1}{2})$
B ${sin}^{- 1} (\frac{\sqrt{2} - 1}{2})$
C ${sin}^{- 1} (\frac{\sqrt{3}}{2})$
D ${sin}^{- 1} (\frac{2}{3 \sqrt{3}})$
Light ray is incident on a prism of angle $A = 60^{\circ}$ and refractive index $μ = \sqrt{2}$ .the angle of incidence at which the emergent ray grazes the surface is given by
A ${sin}^{- 1} (\frac{\sqrt{3} - 1}{2})$
B ${sin}^{- 1} (\frac{1 - \sqrt{3}}{2})$
C ${sin}^{- 1} (\frac{\sqrt{3}}{2})$
D ${sin}^{- 1} (\frac{2}{\sqrt{3}})$
Refractive index of a prism is $\sqrt{7 / 3}$ and the angle of prism is $60^{\circ}$ . The minimum angle of incidence of a ray that will be transmitted through the prism is
A $30^{\circ}$
B $45^{\circ}$
C $15^{\circ}$
D $50^{\circ}$