_S01_030_Q01.png)
A cylinderical tank 1 m in radius rests on a plaform 5 m high. Initially the tank is filled with upto a height of 5m a plug whose area is 10−4cm2 is removed from an orifice on the side of the tank at the bottom.
Calculate (a). Initial speed with which the water flows from the orifice
(b). Initial speed with which the water strikes the ground.
The situation is shown in figure (a) As speed of flow is given by
vH=√(2gh)
or =√2×10×5=10m/s
(b) As initial vertical velocity of water is zero, so its vertical velocity when it hits the ground

vv=√2gh=√2×10×5=10m/s
So the initial speed with which water strikes the ground.
v=√v2Hv2v=10√2=14.1m/s
(c ) When the height of water level above the hole is y, velocity of flow will be v=√2gy and so rate of flow
dVdt=A0v=A0√2gy
or −Ady=(√2gy)A0dt
[As dV=−Ady]
Which on integration improper limits gives
0∫HAdy√2gy=1∫0A0dt⇒t=AA0√2g[√H−√H']
So t=π×1210−4√210[√5−√(5/2)]
=9.2×103s−~2.5h
(d) No, as expression of is indepdent of height of stand.
Topper's Solved these Questions
- FLUIDBOOK - MOTIONCHAPTER - FLUIDEXERCISE - Exercise
27 Videos
- FLUIDBOOK - MOTIONCHAPTER - FLUIDEXERCISE - Exercise-2 (level-I)
10 Videos
- ERRORS , THEORY BOOK - MOTIONCHAPTER - ERRORS , THEORY EXERCISE - EXERCISE 4 (LEVEL -II)
10 Videos
- GEOMETRICAL OPTICSBOOK - MOTIONCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise - 4 | Level-II
55 Videos
Similar Questions
_S01_030_Q01.png)
A cylinderical tank 1 m in radius rests on a plaform 5 m high. Initially the tank is filled with upto a height of 5m a plug whose area is 10−4cm2 is removed from an orifice on the side of the tank at the bottom.
Calculate (a). Initial speed with which the water flows from the orifice
(b). Initial speed with which the water strikes the ground.
View SolutionA cylindrical tank has a radius of 154 cm. It is filled with water to a height of 3 m. If water to a height of 4.5 m is poured into it, what will be the increase in the volume of water in kl?
View Solution
Knowledge Check
A cylindrical tank is filled with water to a level of 3m. A hole is opened at a height of 52.5 cm from bottom. The ratio of the area of the hole to that of cross-sectional area of the cylinder is 0.1. The square of the speed with which water is coming out from the orifice is (Take g=10m/s2)
A50m2/s2B40m2/s2C51.5m2/s2D50.5m2/s2A large tank is filled with water to a depth of 15 m . A spout located 10.0 m above the bottom of the tank is then opened as shown in the figure . With what speed will water emerge from the spout ?
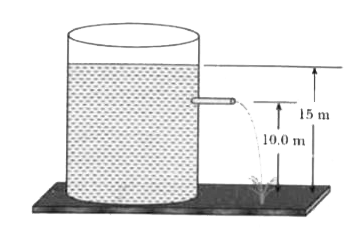 A3.1 m/sB9.9 m/sC14 m/sD17 m/s
A3.1 m/sB9.9 m/sC14 m/sD17 m/sA rectangular tank is placed on a horizontal ground and is filled with water to a height H above the base. A small hole is made on one vertical side at a depth D below the level of the water in the tank. The distance x from the bottom of the tank at which the water jet from the tank will hit the ground is
A2√D(H−D)B2√DHC2√D(H+D)D12√DH
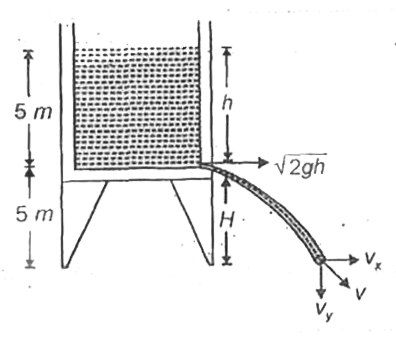
A water tank is placed on a platform of height 5 m high and there is an orifice near the bottom in the wall of tank at 5 m below the level of water. Find the speed with which water will hit the ground [Take g = 10 m/s2 ]
View SolutionA cylindrical tank of cross sectional area a1 is filled with water to a height h. A hole of cross sectional area a2 is made at the bottom. If a1=5a2, then find the
(i) initial velocity with which the water falls in tank.
(ii) initial velocity with which water emerges out from hole.
(iii) time taken to make the tank empty.
View SolutionCalculate the velocity with which water emerges from an orifice in a tank if the gauge pressure is 2×105 N/m before the flow starts.
View SolutionA cylindrical tank of height 2 m is open at the top and has a radius 50 cm. Water is filled in it upto a height 1.75 m. Calculate how long it will take to empty the tank through a hole of radius 0.05 cm in its bottom.
View SolutionThe water level on a tank is 5m high. There is a hole of 1cm2 cross-section at the bottom of the tank. Find the initial rate with which water will leak through the hole. (g=10ms−2)
View Solution
