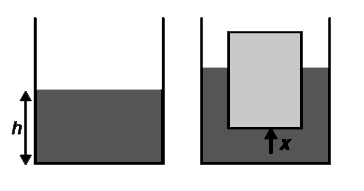
A cylinder of area $300 c m^{2}$ and length 10 cm made of material of specific gravity 0.8 is floated in water with its axis vertical. It is then pushed downward, so as to be just immersed. Calculate the work done by the agent who pushes the cylinder into the water.

Video Solution

Text Solution

Verified by Experts

Weight of the cylinder $= (300 \times 10^{- 4}) \times (10 \times 10^{- 2}) \times 800 kgf = 2.4$ kgf
Let x be the length of the cylinder inside the water. Then by the law of floatation
$2.4 g = (300 \times 10^{- 4} x) \times 100 g$
or $x = 0.08$ m
When completely immersed,
$F_{b}$ (buoyant force)
$= (300 \times 10^{- 4} \times 0.1) \times 1000 \times g = 3 g N$
Thus to immerse the cylinder inside the water the external agent has to push it by $0.02$ m against average upward thrust.
Increase in upward thrust $= 3 g - 2.4 g = 0.6$ g N
Since this increase in upthrust takes place gradually from 0 to $0.6$ g, we may take the average upthrust against which work is done as $0.3$ g N.
work done $0.3 g \times 0.02 = 0.0588$ J

Updated on:21/07/2023

A wire of length l metre made of a material of specific gravity 8 is floating horizontally on the surface of water if it is not wet by water the maximum diameter of the wire upto which it can continue to float is (surface tension of water is T=70xx10^-3Nm^-1)
A1.5
B1.1
C0.75
D0.55
A wire of length l metre made of a material of specific gravity 8 is floating horizontally on the surface of water if it is not wet by water the maximum diameter of the wire upto which it can continue to float is (surface tension of water is T=70xx10^-3Nm^-1)
A1.5
B1.1
C0.75
D0.55
A wire of length $L$ metres, made of a material of specific gravity 8 is floating horizontally on the surface of water. If it is not wet by water, the maximum diameter of the wire (in mm) upto which it can continue to float is (surface tension of water is $T = 70 \times 10^{- 3} N m^{- 1}$ )
A1.5
B1.1
C0.75
D0.55