A beaker of circular ceross sectionof radius 4 cm is filled with mercury up to a height of 10 cm. Find the force exerted by the mercury on the bottom of the beaker. The atmospheric pressure =105Nm−2. Density of mercury =13600kgm−3.Takeg10ms−2
The pressure at the surface=atmospheric presssure =105 N/m2.
The pressure at the bottom 105 N/m2+hρg
=105 N/m2+(0.1 m)(13600kgm3)(10ms2)
=105 N/m2+13600 N/m2=1.136×105 N/m2
The force exerted by the mercury on the bottom
=(1.136×105N/m2)×(3.14×0.04 m×004 m)
=571 N
Topper's Solved these Questions
- FLUIDBOOK - MOTIONCHAPTER - FLUIDEXERCISE - Exercise
27 Videos
- FLUIDBOOK - MOTIONCHAPTER - FLUIDEXERCISE - Exercise-2 (level-I)
10 Videos
- ERRORS , THEORY BOOK - MOTIONCHAPTER - ERRORS , THEORY EXERCISE - EXERCISE 4 (LEVEL -II)
10 Videos
- GEOMETRICAL OPTICSBOOK - MOTIONCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise - 4 | Level-II
55 Videos
Similar Questions
The column of mercury in a barometer is 76 cm Hg. Calculate the atmosphere pressure I the density of mercury =13600kgm−3
(Take g=10ms−2)
View SolutionThe column of mercry in a barometer is 76 cm Hg. Calculate the atmospheric pressure if the density of mercury =13600kgm−3 (Take g=10ms−1B)
View SolutionA glass full of water has a bottom of area 20cm2, top of area 20cm, height 20cm and volume half a litre.
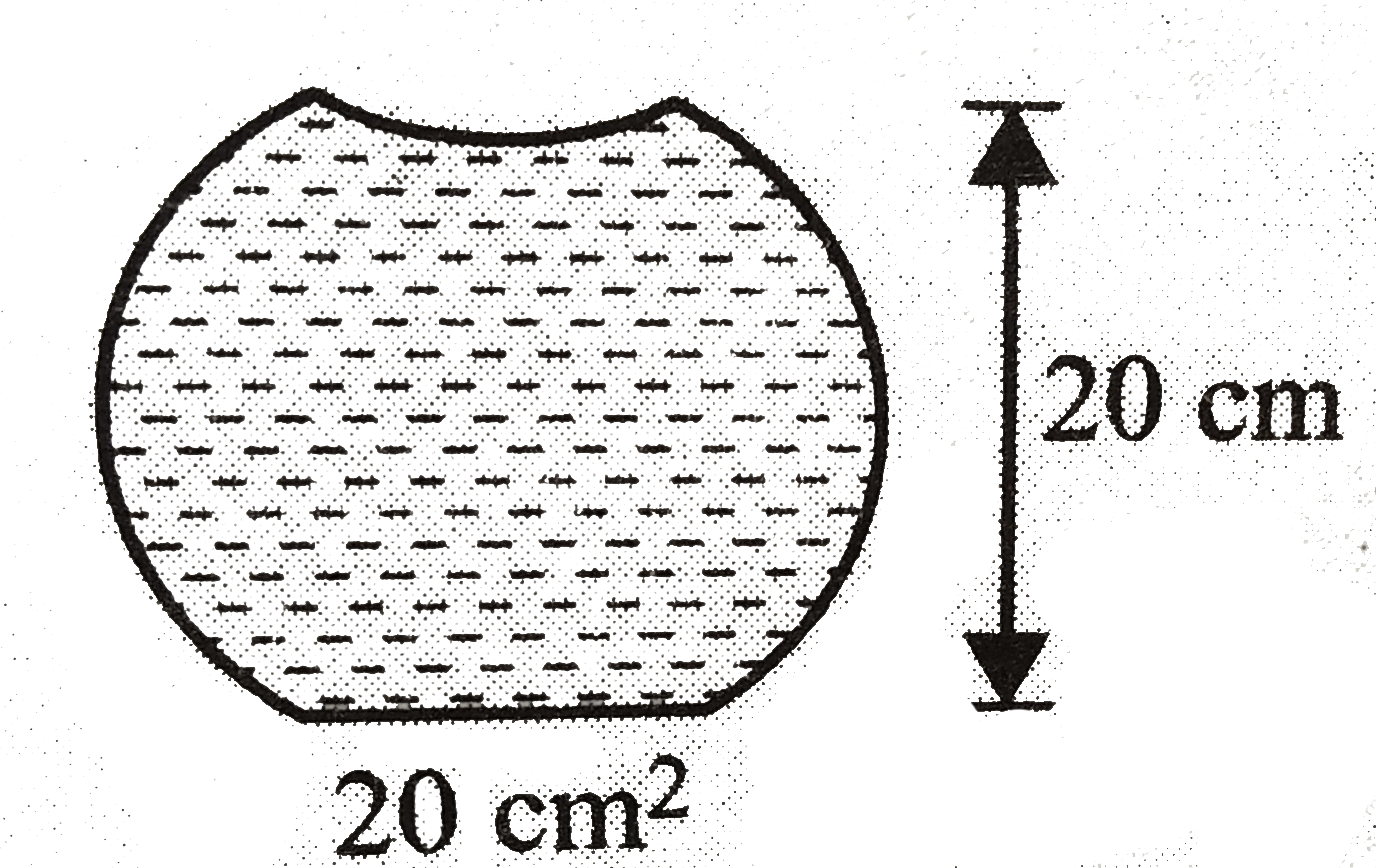
a. Find the force exerted by the water on the bottom.
b. Considering the equilibrium of the v, after. find the resultant force exerted by the side, of the glass on the water. Atmospheric pressure =1.0×105N/m2. Density of water =1000kg/m−3 and g=10m/s2
View SolutionA vessel full of water has a bottom of area 20cm2, top of area 20cm2, height 20 cm and volume half a litre as shown in figure.
(a) find the force exerted by the water on the bottom.

(b) considering the equilibrium of the water, find the resultant force exerted by the sides of the glass vessel on the water. atmospheric pressure =1.0×105N/m2. density of water =1000kg/m3 and g=10m/s2
View Solution76 cm of mercury column is a measure of atmospherice pressure. Express it is N/m2 Given density of mercury is 13.6×103kg/m3
View SolutionWater is filled in a flask up top a heightof 20 cm. The bottom of the flask is circular with radius 10 cm.If the atmospheric pressure is 1.01×105 Pa, find the force exerted by the water on the bottom. Take g=10ms−2 and density of water =1000 kgm^-3.
View SolutionWater is filled in a flask upto a height of 20cm. The bottom of the flask is circular with radius 10cm. If the atmospheric pressure is 1.013×105 Pa, find the force exerted by the water on the bottom . Take g=10ms−2 and density of water =1000kgm−3.
View SolutionConvert a pressure of 76cm of mercury into Nm−2. Density of mercury is 13.6gm/cc.
View SolutionConsider a small surface area of 1 mm2 at the top of a mercury drop of radius 4.0 mm. Find the force exerted on this area (a) by the air above it (b) by the mercury below it and (c) by the mercury surface in contact with it. Atmospheric pressure =1.0x105Pa and surface tension of mercuru =0.465Nm−1. Neglect the effect fo gravity. Assume all numbers to be exact.
View SolutionCalculate the equivalent height of water barometer if the pressure recorded by mercury barometer is 76 cm. Density of mercury is 13600kgm−3 and density of water is 1000kgm−3.
View Solution

