One mole of a ideal monoatomic gas (CV.m=1.5R) is subjected to the following sequence of steps :
(a) The gas is heated reversibly at constant pressure of 101.325 kPa from 298 K to 373 K.
(b) Next, the gas is expanded reversibly and isothermally to double its volume.
(c) Finally, the gas is cooled reversibly and adiabatically to 308 K.
Calculate q, w, ΔUandΔH for the overall process.
To solve the problem step by step, we will calculate the heat (q), work (w), change in internal energy (ΔU), and change in enthalpy (ΔH) for each of the three steps in the process.
Step 1: Heating at Constant Pressure (Isobaric Process)
1. Given Data:
- Number of moles (n) = 1 mole
- Initial temperature (T1) = 298 K
- Final temperature (T2) = 373 K
- Constant pressure (P) = 101.325 kPa
- Molar heat capacity at constant volume (C_V,m) = 1.5 R
2. Calculate C_P:
CP=CV+R=1.5R+R=2.5R
3. Calculate ΔH:
ΔH=nCP(T2−T1)=1×2.5R×(373−298)
=2.5×8.314×75=1558.88J
4. Calculate ΔU:
ΔU=nCV(T2−T1)=1×1.5R×(373−298)
=1.5×8.314×75=935.33J
5. Calculate Work Done (w):
w=−PextΔV=−nR(T2−T1) (since P is constant)
=−1×8.314×(373−298)=−623.55J
Step 2: Isothermal Expansion to Double Volume
1. Given Data:
- Initial volume (V1) and final volume (V2 = 2V1)
- Temperature (T) = 373 K (constant)
2. Calculate Work Done (w):
w=−nRTln(V2V1)=−1×8.314×373×ln(2)
=−2149.71J
3. Calculate ΔU:
Since the process is isothermal for an ideal gas, ΔU = 0.
4. Calculate q:
ΔU=q+w⟹q=ΔU−w=0+2149.71=2149.71J
5. Calculate ΔH:
For isothermal processes, ΔH = ΔU + PΔV, but since ΔU = 0, we can conclude:
ΔH=0
Step 3: Adiabatic Cooling to 308 K
1. Given Data:
- Initial temperature (T1) = 373 K
- Final temperature (T2) = 308 K
2. Calculate q:
Since the process is adiabatic, q = 0.
3. Calculate ΔU:
ΔU=nCV(T2−T1)=1×1.5R×(308−373)
=1.5×8.314×(−65)=−810.63J
4. Calculate Work Done (w):
Since q = 0, we have:
w=ΔU=−810.63J
5. Calculate ΔH:
ΔH=nCP(T2−T1)=1×2.5R×(308−373)
=2.5×8.314×(−65)=−1351.03J
Overall Process Calculations
1. Total q:
qtotal=q1+q2+q3=1558.88+2149.71+0=3708.59J
2. Total w:
wtotal=w1+w2+w3=−623.55−2149.71−810.63=−3583.89J
3. Total ΔU:
ΔUtotal=ΔU1+ΔU2+ΔU3=935.33+0−810.63=124.70J
4. Total ΔH:
ΔHtotal=ΔH1+ΔH2+ΔH3=1558.88+0−1351.03=207.85J
Final Answers:
- qtotal=3708.59J
- wtotal=−3583.89J
- ΔUtotal=124.70J
- ΔHtotal=207.85J
- Number of moles (n) = 1 mole
- Initial temperature (T1) = 298 K
- Final temperature (T2) = 373 K
- Constant pressure (P) = 101.325 kPa
- Molar heat capacity at constant volume (C_V,m) = 1.5 R
CP=CV+R=1.5R+R=2.5R
ΔH=nCP(T2−T1)=1×2.5R×(373−298)
=2.5×8.314×75=1558.88J
ΔU=nCV(T2−T1)=1×1.5R×(373−298)
=1.5×8.314×75=935.33J
w=−PextΔV=−nR(T2−T1) (since P is constant)
=−1×8.314×(373−298)=−623.55J
- Initial volume (V1) and final volume (V2 = 2V1)
- Temperature (T) = 373 K (constant)
w=−nRTln(V2V1)=−1×8.314×373×ln(2)
=−2149.71J
Since the process is isothermal for an ideal gas, ΔU = 0.
ΔU=q+w⟹q=ΔU−w=0+2149.71=2149.71J
For isothermal processes, ΔH = ΔU + PΔV, but since ΔU = 0, we can conclude:
ΔH=0
- Initial temperature (T1) = 373 K
- Final temperature (T2) = 308 K
Since the process is adiabatic, q = 0.
ΔU=nCV(T2−T1)=1×1.5R×(308−373)
=1.5×8.314×(−65)=−810.63J
Since q = 0, we have:
w=ΔU=−810.63J
ΔH=nCP(T2−T1)=1×2.5R×(308−373)
=2.5×8.314×(−65)=−1351.03J
qtotal=q1+q2+q3=1558.88+2149.71+0=3708.59J
wtotal=w1+w2+w3=−623.55−2149.71−810.63=−3583.89J
ΔUtotal=ΔU1+ΔU2+ΔU3=935.33+0−810.63=124.70J
ΔHtotal=ΔH1+ΔH2+ΔH3=1558.88+0−1351.03=207.85J
- qtotal=3708.59J
- wtotal=−3583.89J
- ΔUtotal=124.70J
- ΔHtotal=207.85J
Topper's Solved these Questions
- THERMODYNAMICSBOOK - MOTIONCHAPTER - THERMODYNAMICSEXERCISE - EXERCISE - 4 (LEVEL - I)
21 Videos
- THERMODYNAMICSBOOK - MOTIONCHAPTER - THERMODYNAMICSEXERCISE - EXERCISE - 4 (LEVEL - II)
19 Videos
- THERMODYNAMICSBOOK - MOTIONCHAPTER - THERMODYNAMICSEXERCISE - EXERCISE - 2 (LEVEL-II ASSERTION REASON)
6 Videos
- THERMOCHEMISTRY BOOK - MOTIONCHAPTER - THERMOCHEMISTRY EXERCISE - Exercise - 4 Level-II
8 Videos
Similar Questions
One mole of an ideal monoatomic gas (CV.M=1.5R) is subjected to the following sequence of steps :
(a) The gas is heated reversibly at constant pressure of 1 atm from 298 K to 373 K.
(b) Next, the gas is heated reversibly and isothermally to double its volume.
(c) Finally , the gas is cooled reversibly and adiabatically to 308 K .
Calcuated q, w, ΔH for the overall porcess.
View SolutionAn ideal gas at 300K is expanded isothermally to double its volume, then pressure of the gas will be
View Solution
Knowledge Check
One mole of an ideal gas expands isothermally to double its volume at 27∘C . The work done by the gas is nearly
A2760calB414calC1380calD600calOne mole of an ideal and monoatomic gas is expanded reversibly and isothermally at 298K temperature according to the given diagram, calculate work done.
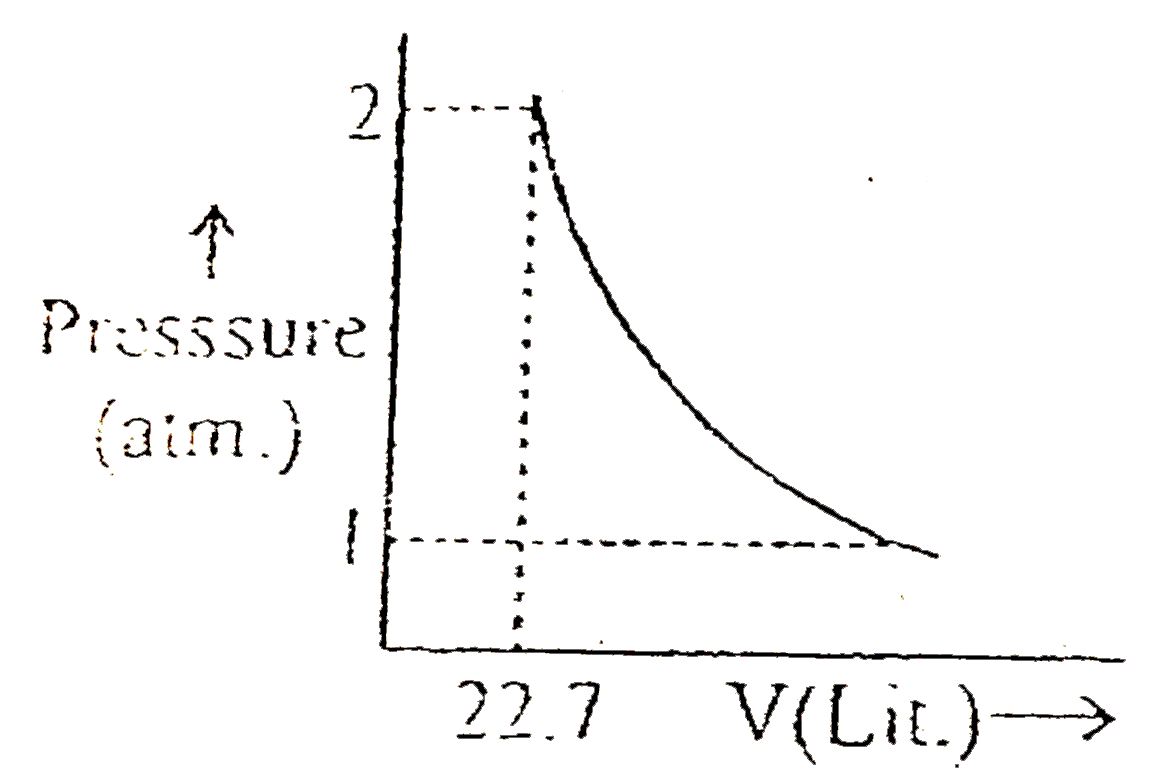 A−1717.46JB+1717.46JC−171.746JD+171.746J
A−1717.46JB+1717.46JC−171.746JD+171.746JCalculate the final temperature of a monoatomic ideal gas that is compressed reversible and adiabatically from 16L to 2L at 300K:
A600KB1044.6KC1200KD2400K
An ideal monoatomic gas at 300K expands adiabatically to twice its volume. What is the final temperature?
View SolutionA gas expands isothermally and reversibly. The work done by the gas is -
View SolutionOne mole of an ideal gas expands reversibly and isothermally at 300 K from 5dm3 to 50dm3. The work done by the gas for the process is equal to
View SolutionOne mole of an ideal gas at 25∘C is subjected to expand reversible ten times of its intial volume. The change in entropy of expansion is
View SolutionOne mole of an ideal gas (Cv,m=52R) at 300 K and 5 atm is expanded adiabatically to a final pressure of 2 atm against a constant pressure of 2 atm. Final temperature of the gas is :
View Solution
