Solve the following problem graphically:Minimise and Maximise Z=3x+9y . . . (1)subject to the constraints: x+3y≤60 . . . (2) x+y≥10 . . . (3) x≤y . . . (4) x≥0,y≥0 . . . (5)
Video Solution
Text Solution
Let Z=3x+9y....(1)
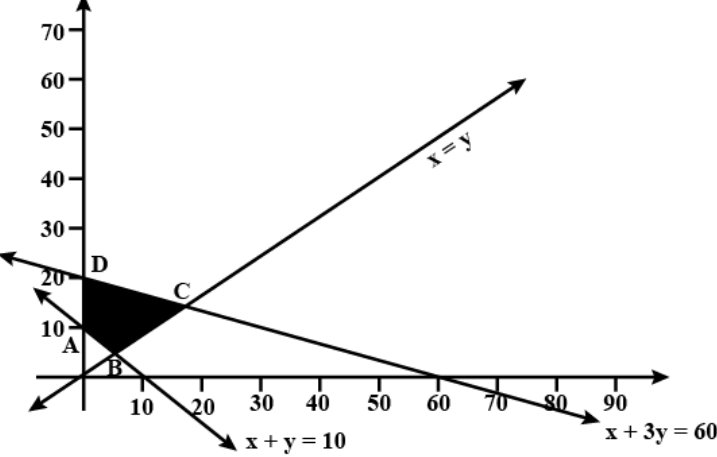
Converting inequalities to equalities x+3y=60 to solve these equation we get the required points are (0,20),(60,0)
x+y=10 we get required points are (0,10),(10,0)
and x−y=0 we get required points are (0,0),(10,10),(20,20)
Plot the graph for the set of points
The graph shows the bounded feasible region. ABCD, with corner points A=(10,0),B=(5,5),C=(15,15) and D=(0,20)To find maximum and minimum
⎡⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢⎣Corner pointZ=3x+9yA=(0,10)90B=(5,5)60C=(15,15)180D=(0,20)180⎤⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥⎦
From the graph maximum value of X occurs at two corner points C(15,5) and D(0,20) with value 180 and minimum occurs at point B(5,5) with value 60.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
Solve the Following Linear Programming Problem graphically : Maximise Z=3x+4ysubject to the constraints : x+y≤4,x≥0,y≥0.
A14B15C16D17Solve the following linear programming problem graphically :Minimise Z=200x+500y. . . (1)subject to the constraints:x+2y≥10 . . .(2)3x+4y≤24 . . .(3)x≥0,y≥0 . . .(4)
A(Z)=(4,3)=2300B(Z)=(5,4)=2400C(Z)=(6,2)=2500D(Z)=(5,3)=2550
Solve the following problem graphically: Minimise and Maximise z = 2x + 6y Subject to the constraints: x+2y≤10, x+y≤7, x≥2, x≥0, y≥0
View SolutionSolve the following problem graphically,Maximise and minimise z=5x+10y, subject to the constraints x+2y≤120,x+y≥60,−2y≥0andx,y≥0.
View SolutionSolve the following L.P.P graphically
Minimise and maximise z = 3x + 9y
Subject to the constraints x+3y≤60
x+y≥10
x≤y
x≥0,y≥0
View SolutionSolve the following linear programming problem graphically: Maximise Z=4x+y . . . (1) , subject to the constraints:x+y≤50 . . .(2), 3x+y≤90 . . .(3) , x≥0,y≥0 . . .(4)
View SolutionMaximise z = 8x + 9y subject to the constraints given below : 2x+3y≤6 3x2y≤6 y≤1 x,y≥0
View SolutionMaximise Z=3x+4y
Subject to the constraints
x+y≤4,x≥0,y≥0
View Solution
