If the extremities of a line segment of length l moves in two fixed perpendicular straight lines, then the locus of the point which divides this line segment in the ratio 1 : 2 is-
a parabola
an ellipse
a hyperbola
None of these
The correct Answer is:2
Let the two fixed perpendicular straight lines be the co-ordinate axis
let P(h, k) be the point whose locus is required
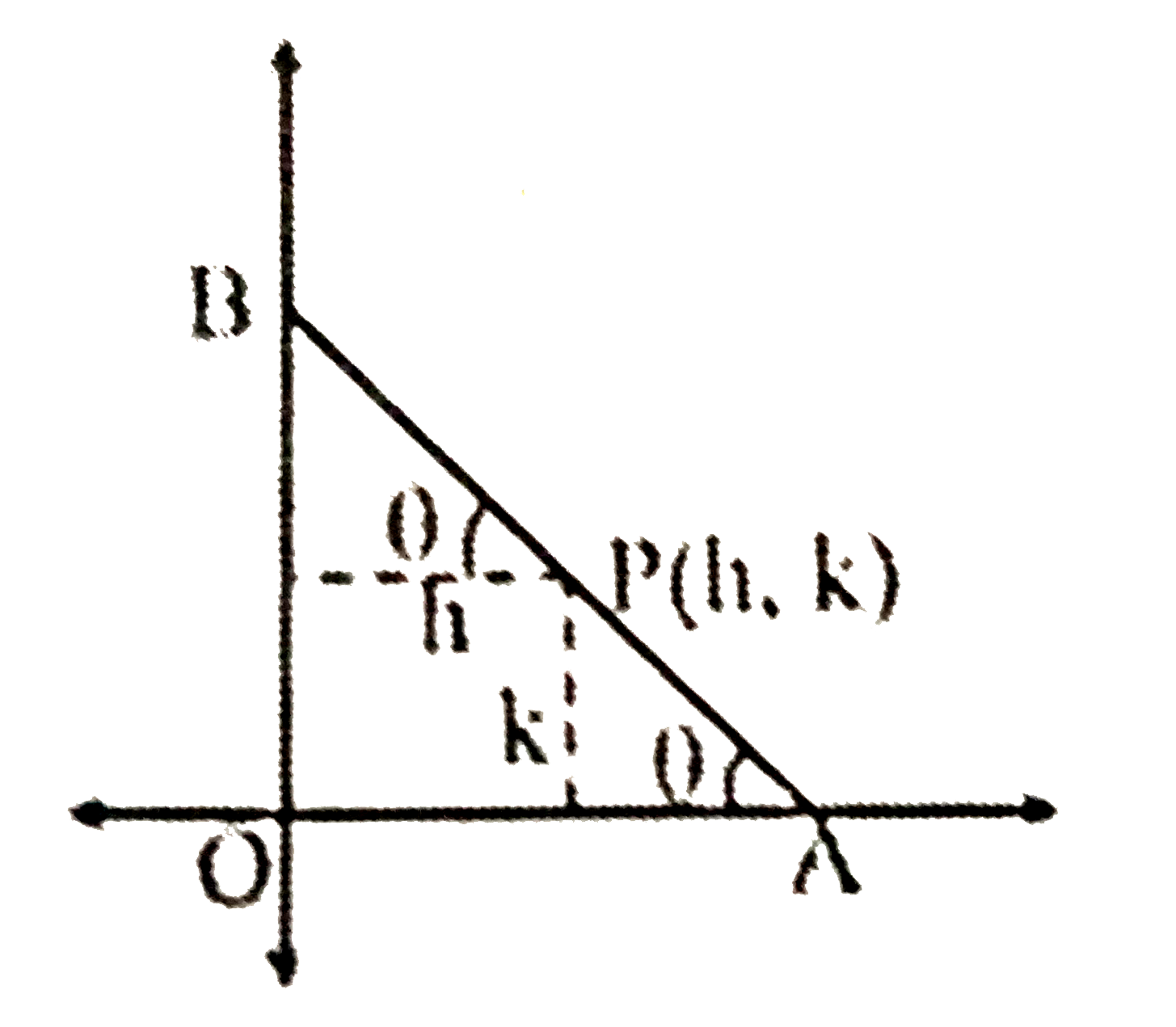
let PA : PB = 1 : 2
Then PA=l3 and PB = 2l3
k=l3sinθor3k=lsinθ.....(i)
and h=2l3cosθor3h2=lcosθ....(ii)
Sqauring and adding (i) and (ii) we get
9k2+9h24=l2
∴ locus 9x2+36y2=4l2
Which is an eclipse
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
A variable straight line of slope 4 intersects the hyperbola xy=1 at two points. The locus of the point which divides the line segment between these two points in the ratio 1:2 is
A16x2+10xy+y2=2B16x2−10xy+y2=2C16x2+10xy+y2=4Dnone of these
A line segment AB of length '2' moves with its ends on the axes. The locus of the point P which divides the segment in the ratio 1:1 is
View SolutionA straight line segment of length / moves with its ends axis and y-axis. The locus of the point which x-axis and y-a divides the line segment in the ratio 1: 2 18s on
View SolutionThe ends of a rod of length l move on two mutually perpendicular lines. Find the locus of the point on the rod which divides it in the ratio 1 : 2.
View SolutionA line of fixed length a+b moves so that its ends are always on two fixed perpendicular straight lines. Then the locus of the point which divides this line into portions of length aandb is a/an ellipse (b) parabola straight line (d) none of these
View SolutionA line segment AB of length a moves with its ends on the axes.The locus of the point P which divides the segment in the ratio 1:2 is
View SolutionThe ends of a rod of length l move on two mutually perpendicular lines. The locus of a point on the rod which divides it in the ratio 1:2 is ………...
View SolutionFind the coordinates of the point which divides the line segment joining A(-2, 2) and B(2, 8) in the ratio 3 : 1.
View Solution
