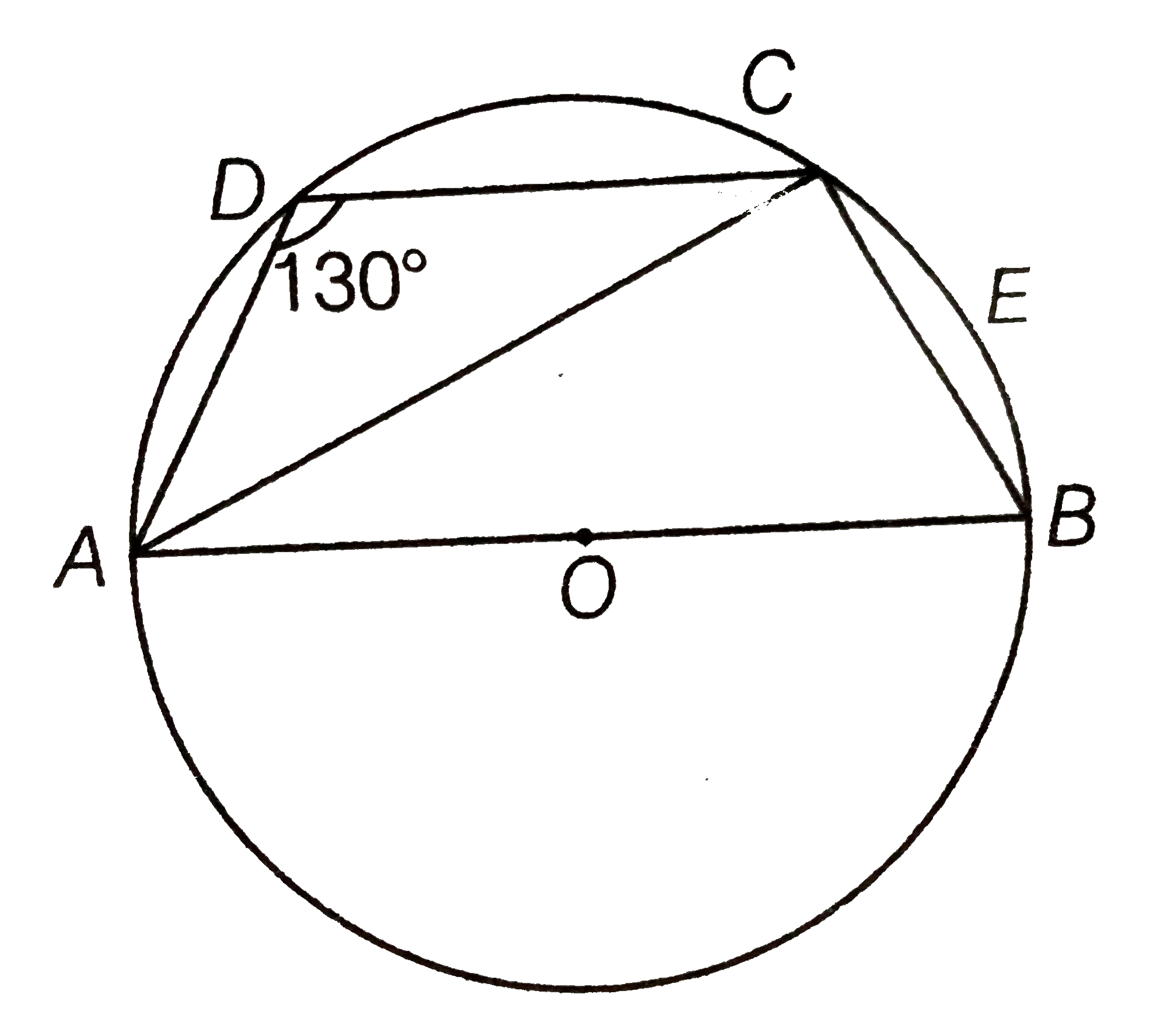
In Figure, $A B C D$ is a cyclic quadrilateral whose side $A B$ is a diameter of the circle through $A, B, C, D .$ If $(∠ A D C) = 130^{0},$ find $∠ B A C$
$In Figure, A B C D is a cyclic quadrilateral whose side A B is a diameter of the circle through A ,\ B ,\ C ,\ Ddot If (/A D C)=130^0,find /B A C$

Video Solution

Text Solution

Verified by Experts

Draw a quadrilateral ABCD inscribed in a circle having centre O. Given, $∠ A D C = 130^{\circ}$
Since, ABCD is a quadrilateral inscribed in a circle, therefore ABCD becomes a cyclic quadrilateral.
$∵ Since, the sum of opposite angles of a cyclic quadrilateral is 180^{\circ}$ .
$∴ ∠ A D C + ∠ A B C = 180^{\circ}$
$\Rightarrow 130^{\circ} + ∠ A B C = 180^{\circ}$
$\Rightarrow ∠ A B C = 50^{\circ}$
Since, AB is a diameter of a circle, then AB subtends an angle to the circle is right angle.
$∴ ∠ A C B = 90^{\circ}$
In $Δ A B C, ∠ B A C + ∠ A C B + ∠ A B C = 180^{\circ}$ [by angle sum property of a triangle]
$\Rightarrow ∠ B A C + 90^{\circ} + 50^{\circ} = 180^{\circ}$
$\Rightarrow ∠ B A C = 180^{\circ} - (90^{\circ} + 50^{\circ})$
$= 180^{\circ} - 140^{\circ} = 40^{\circ}$

Updated on:21/07/2023