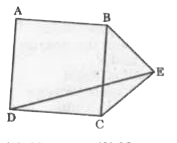
In figure, ∠ADC=130∘ and chord BC=chord BE. Find ∠CBE.
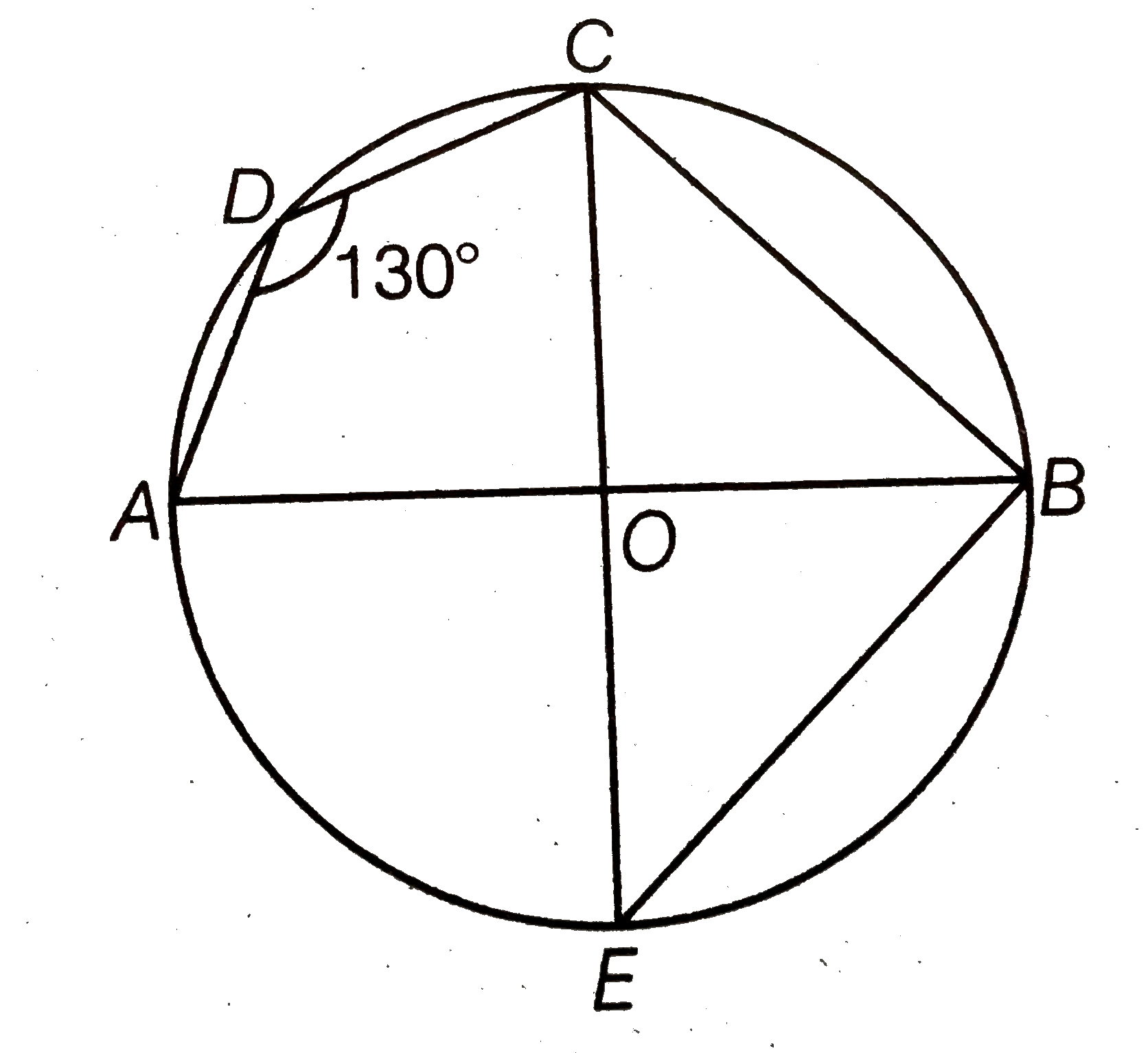
We have, ∠ADC=130∘ and chord BC=chord BE. Suppose, we consider the points A, B, C and D form a cyclic quadrilateral.
Since, the sum of opposite angles of a cyclic quadrilateral ADCB is 180∘.
∴∠ADC+∠OBC=180∘
⇒130∘+∠OBC=180∘
⇒∠OBC=180∘−130∘=50∘
InΔBOCandΔBOE,
BC=BE [given equal chord]
OC=OE [both are the radius of a circle]
and OB=OB [common side]
∴ΔBOC≅ΔBOE [by SSS songruence rule]
⇒∠OBC=∠OBE=50∘ [by CPCT]
Now, ∠CBE=∠CBO+∠EBO
=50∘+50∘=100∘
Topper's Solved these Questions
- CIRCLESBOOK - NCERT EXEMPLARCHAPTER - CIRCLESEXERCISE - Exercise 10.4
2 Videos
- Areas of Parallelograms and TrianglesBOOK - NCERT EXEMPLARCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Areas Of Parallelograms And Triangles
34 Videos
- CONSTRUCTIONSBOOK - NCERT EXEMPLARCHAPTER - CONSTRUCTIONSEXERCISE - Long Answer Type Questions
5 Videos
Similar Questions
Knowledge Check
In the given figure, AB is the diameter of the circle, ∠ADC=120∘. Find ∠CAB:
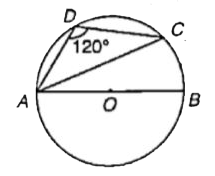 A20∘B30∘C40∘Dcan't be determined
A20∘B30∘C40∘Dcan't be determinedIn the given figure, ABCD is a rhombos and BCE is an isosceles triangle, with BC = CE, ∠CBE=84∘ and ∠ADC=78∘. What is the value (in degree) of ∠DEC ?
 A1) 20B2) 28C3) 33D4) 36
A1) 20B2) 28C3) 33D4) 36
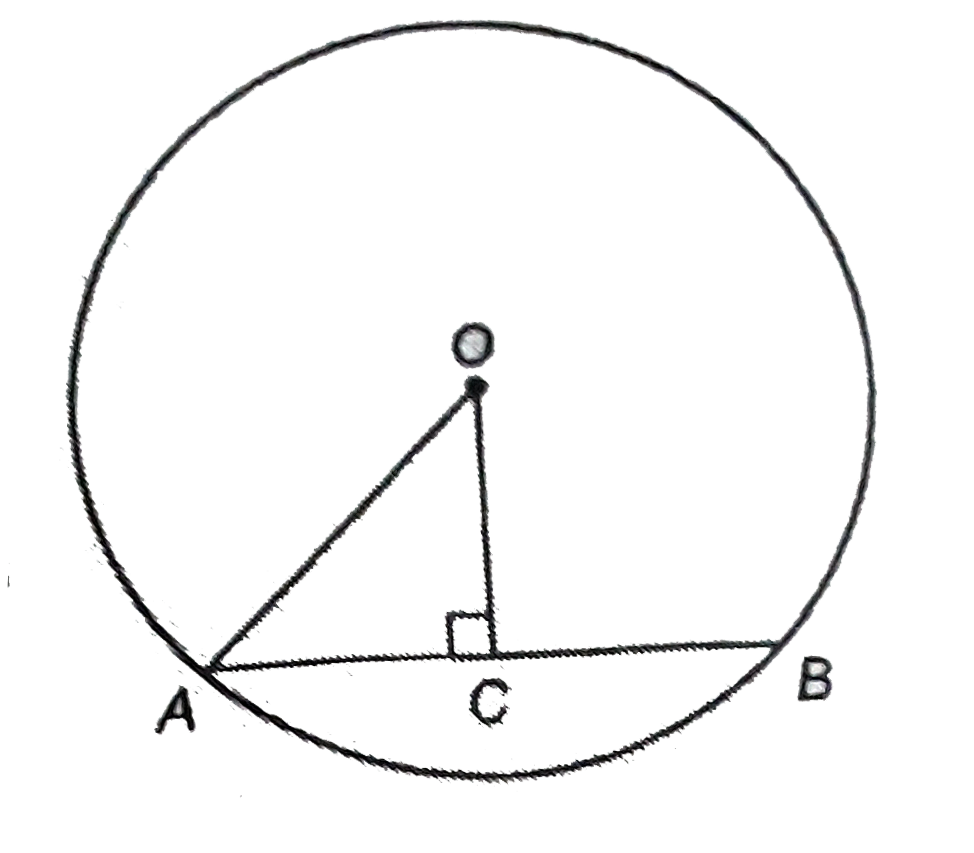
The radius of a circle is 10 cm and the perpendicular form the centre to a chord is 8cm. Find the length of the chord.
(ii) The radius of a circle is 10 cm. its one chord is 16 cm long. Find the perpendicular distance of this chord form the centre.
(iii) in the adjoining figure O is the centre of circle. the radius of circle is 17 cm . if OC=8cm, then find the length of chord AB.
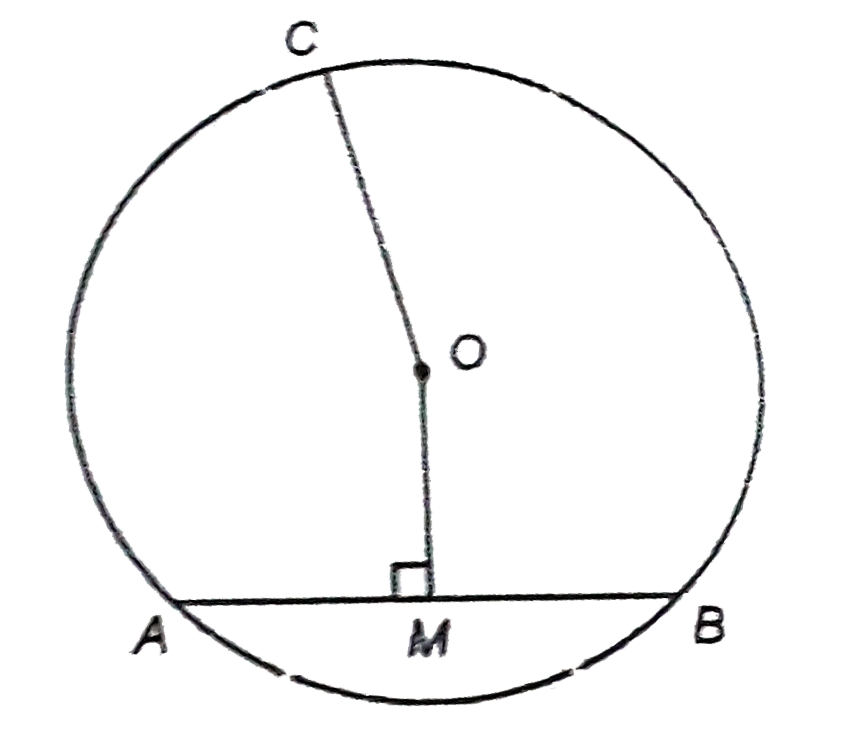
(iv) In the adjoining figure, OM⊥AB, radius OC=5cm and chord AB=8cm.Find the length of OM.
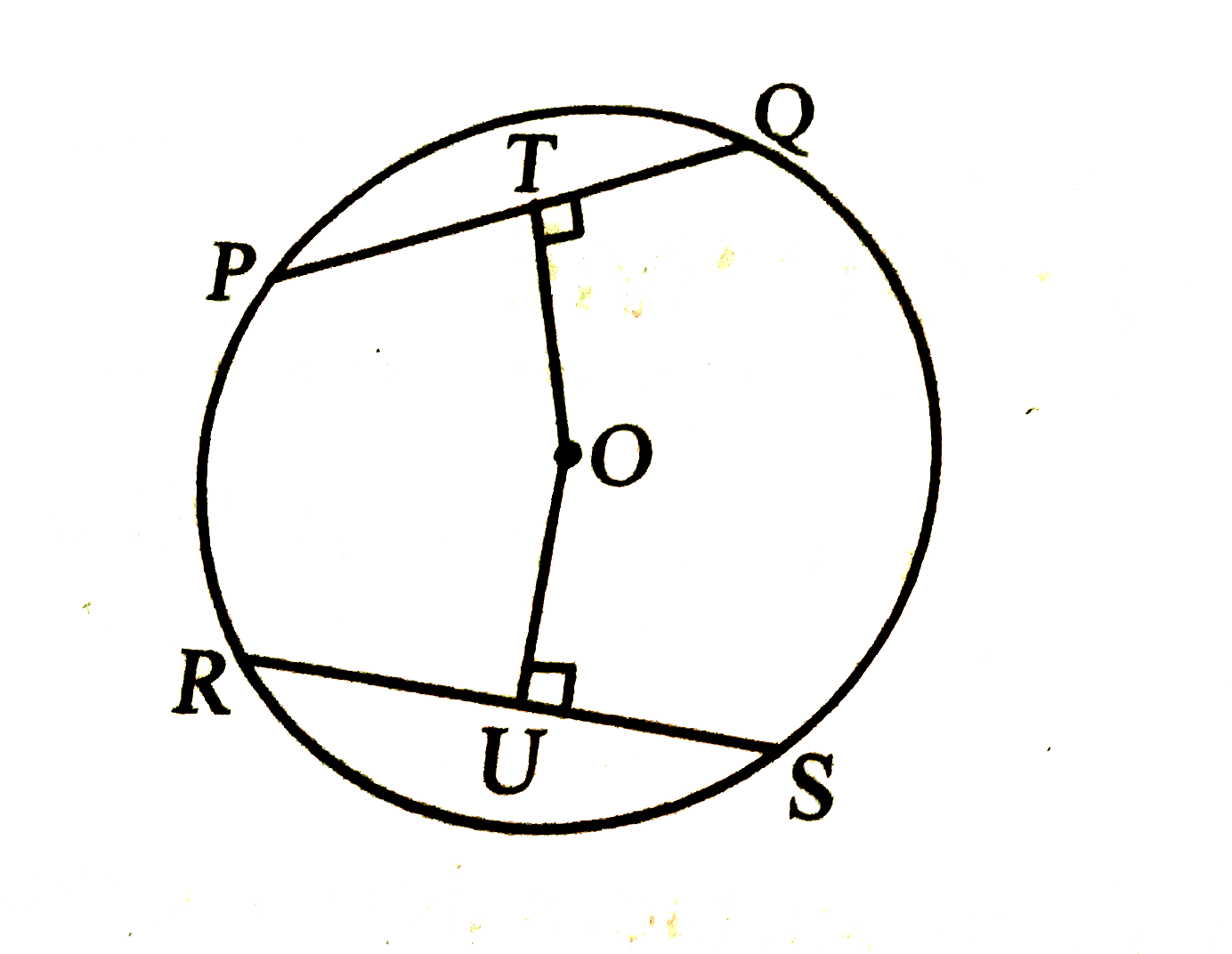
View SolutionIn the given figure, O is the center and chord PQ = Chord RS. If OT = 5 cm, then find OU.
View SolutionIn the figure, ¯¯¯¯¯¯AB || ¯¯¯¯¯¯CDand¯¯¯¯¯¯AD || ¯¯¯¯¯¯BC. If ∠ABC=110∘,∠ACD=30∘, then find ∠ADC.

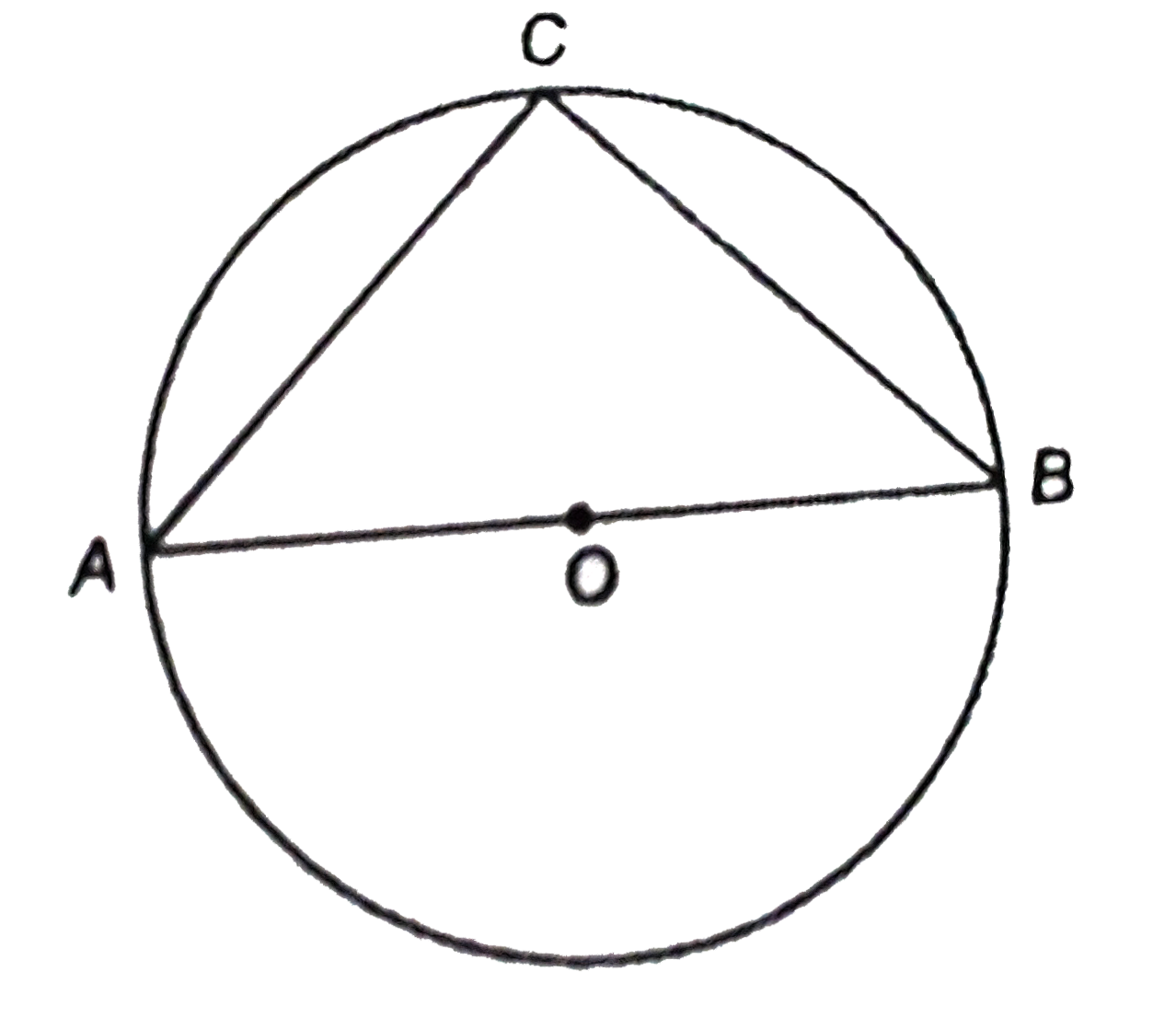
View SolutionO is the centre of a circle of diameter AB. If chord AC= chord BC, then find the value of ∠ABC.
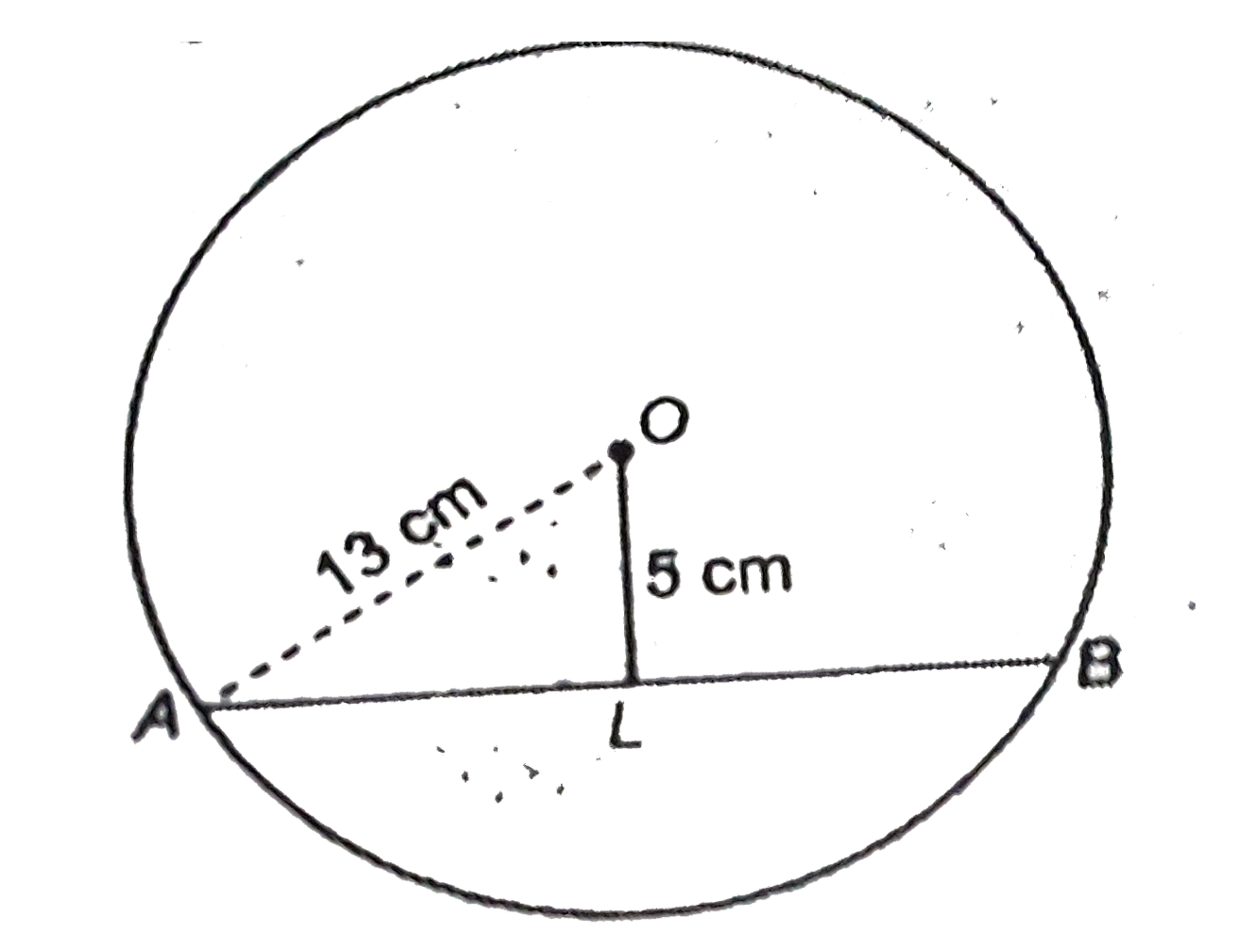
View SolutionIn the given figure , find the length of chord AB .
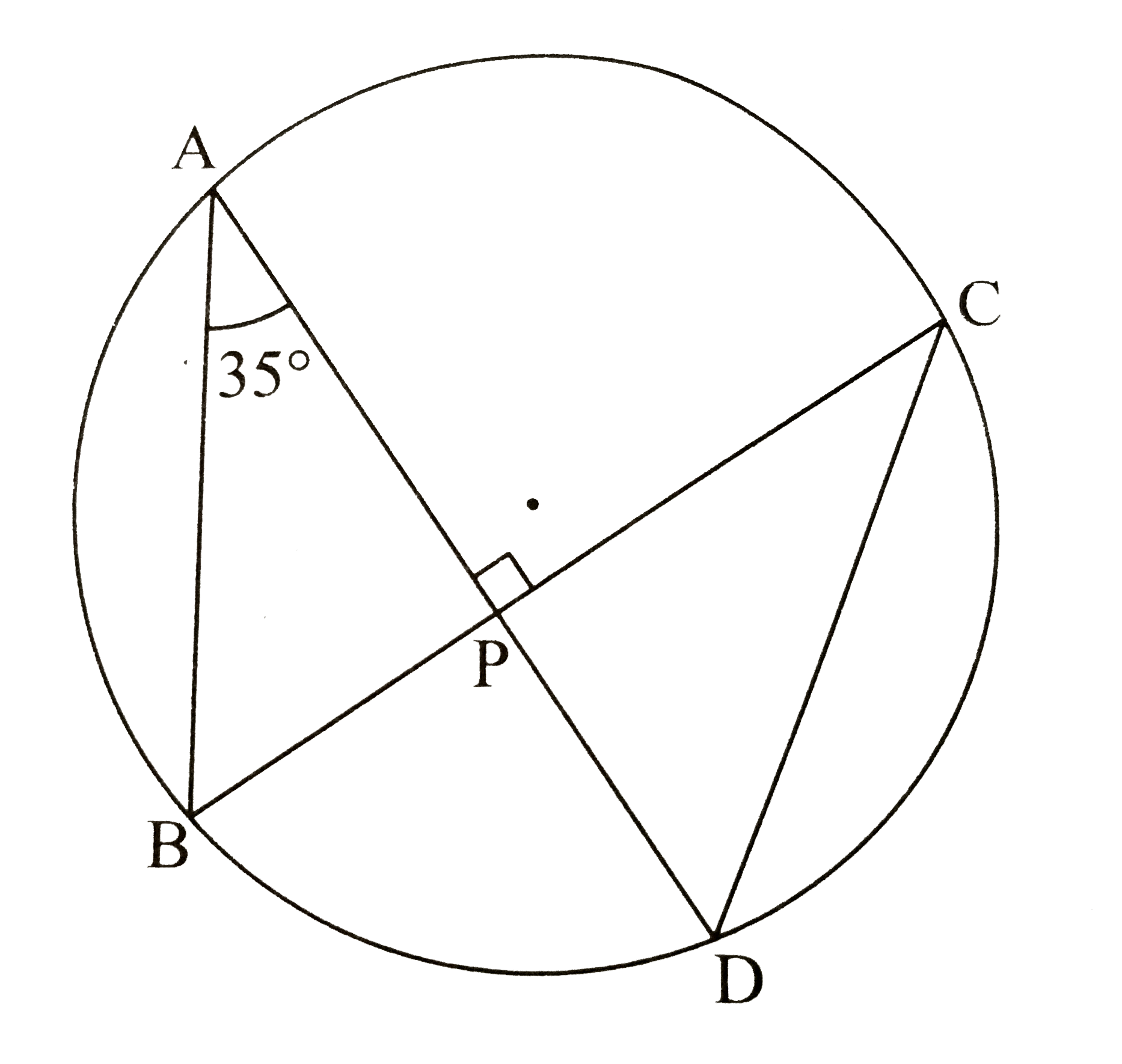
View SolutionIn the figure, chords AD and BC intersect each other at right angles at a point P. If ∠DAB=35∘, then ∠ADC=
View Solution