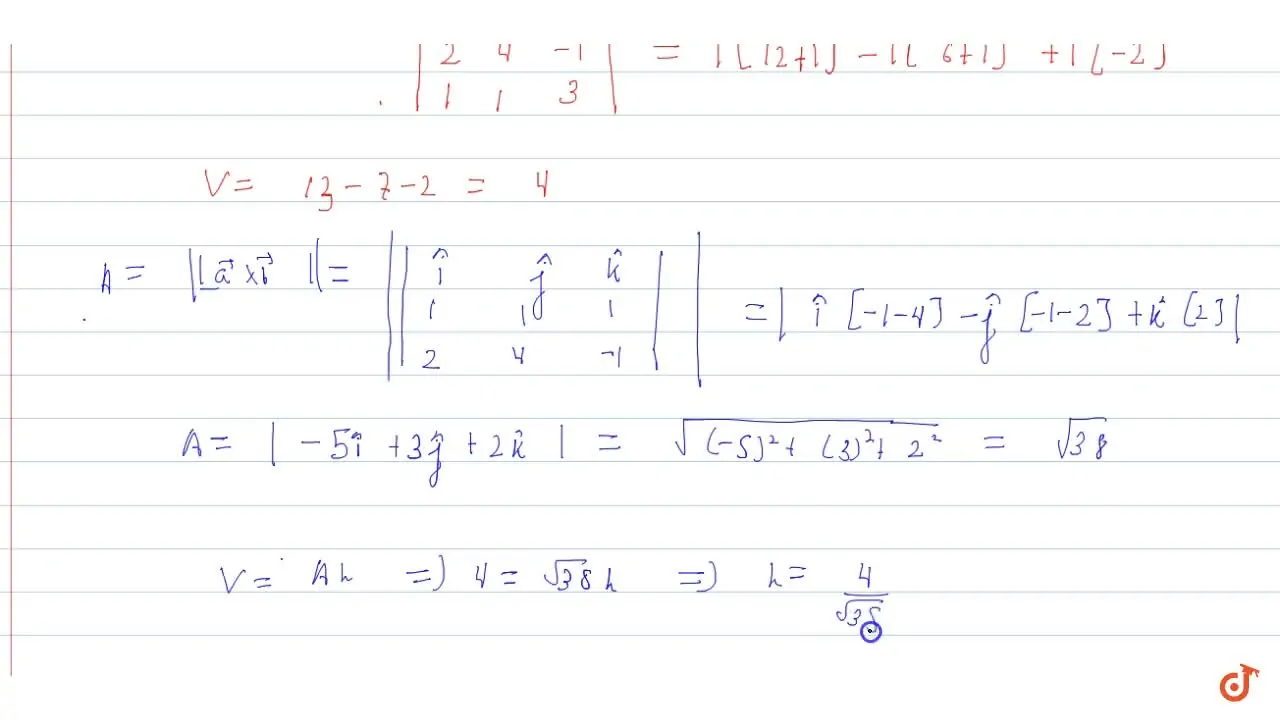Find the altitude of a parallelepiped determined by the vectors →a,→band→c, if the base is taken as the parallelogram determined by →aand→b,and if →a=ˆi+ˆj+ˆk,→b=2ˆi+4ˆj−ˆkand→c=ˆi+ˆj+3ˆk.
Given,
→a=ˆi+ˆj+ˆk,→b=2ˆi+4ˆj−ˆkand→c=ˆi+ˆj+3ˆk.
and the base is a parallelogram determined by →a
and →b
The altitude of a parallelopiped is given by
h=VolumeAreaofbase=c⋅(a×b)|a×b|
c⋅(a×b)=⎡⎢⎣11311124−1⎤⎥⎦
=1(−1−4)−1(−1−2)+3(4−2)
=−5+3+6=4
a×b=⎡⎢⎣ˆiˆjˆk11124−1⎤⎥⎦
=ˆ1(−1−4)−ˆj(−1−2)+ˆk(4−2)
=−5ˆi+3ˆj+2ˆk
|a×b|=√(−5)2+(3)2+(2)2=√38
Hence,
h=4√38
Related Playlists
Similar Questions
Find the altitude of a parallelepiped determined by the vectors →a,→band→c, if the base is taken as the parallelogram determined by →aand→b,and if →a=ˆi+ˆj+ˆk,→b=2ˆi+4ˆj−ˆkand→c=ˆi+ˆj+3ˆk.
View SolutionFind →a.(→b×→c) if →a=2ˆi+ˆj+3ˆk, →b=−ˆi+2ˆj+ˆk and →c=3ˆi+ˆj+2ˆk.
View SolutionFind [→a →b →c] , when : →a=2ˆi−3ˆj, →b=ˆi+ˆj−ˆk and →c=3ˆi−ˆk.
View SolutionFind the projection of →b+→c on →a , where →a=2ˆi−2ˆj+ˆk, →b=ˆi+2ˆj−2ˆk and →c=2ˆi−ˆj+4ˆk.
View SolutionFind the projection of →b+ →c on →a where →a=2ˆi− 2ˆj+ ˆk, →b= ˆi+ 2ˆj− 2ˆk and →c=2ˆi− ˆj+ 4ˆk
View SolutionIf →a=3ˆi−ˆj+2ˆk and →b=2ˆi+ˆj−ˆk then find(→a×→b)→a.
View SolutionIf →a=3ˆi−ˆj−4ˆk, →b=−2ˆi+4ˆj−3ˆk and →c=ˆi+2ˆj−ˆk,find ∣∣3→a−2→b+4→c∣∣.
View SolutionFind the volume of the parallelepiped whose coterminous edges are represented by the vectors: →a=2ˆi+3ˆj+4ˆk,→b=ˆi+2ˆj−ˆk,→c=3ˆi−ˆj+2ˆk →a=2ˆi+3ˆj+4ˆk,→b=ˆi+2ˆj−ˆk,→c=3ˆi−ˆj−2ˆk →a=11ˆi,→b=2ˆj−ˆk,→c=13ˆk →a=ˆi+ˆj+ˆk,→b=ˆi−ˆj+ˆk,→c=ˆi+2ˆj−ˆk
View SolutionIf →a=3ˆi−ˆj−4ˆk, →b=−2ˆi+4ˆj−3ˆk and →c=ˆi+2ˆj−ˆk, find ∣∣3→a−2→b+4→c∣∣.
View SolutionIf →a=ˆi−ˆj and →b=−ˆj+ˆk find the projection of →aon →b.
View Solution