Question

(Manufacturing problem) A
manufacturing company makes two models A and B of a product. Each piece of
Model A requires 9 labour hours for fabricating and 1 labour hour for
finishing. Each piece of Model B requires 12 labour hours for fabricating and
3 labour hours for finishing. For fabricating and finishing, the maximum
labour hours available are 180 and 30 respectively. The company makes a
profit of Rs 8000 on each piece of model A and Rs 12000 on each piece of
Model B. How many-pieces of Model A and Model B should be manufactured per
week to realise a maximum profit? What is the maximum profit per week?

Explanation

Solution:

Suppose x is the number of pieces of Model A and y is the number of pieces of
Model B. Then
Total profit (in Rs) =`8000 x +12000 y`

Let Z=`8000 x+12000 y`

We now have the following mathematical model for the given problem.

Maximise Z=`8000 x+12000 y ldots (1)`

subject to the constraints :

`9 x+12 y leq 180` (Fabricating constraint)

i.e. `3 x+4 y leq 60 ldots`(2)

`x+3 y leq 30` (Finishing constraint) ...(3)

`x geq 0, y geq 0` (non-negative constraint) ...(4)

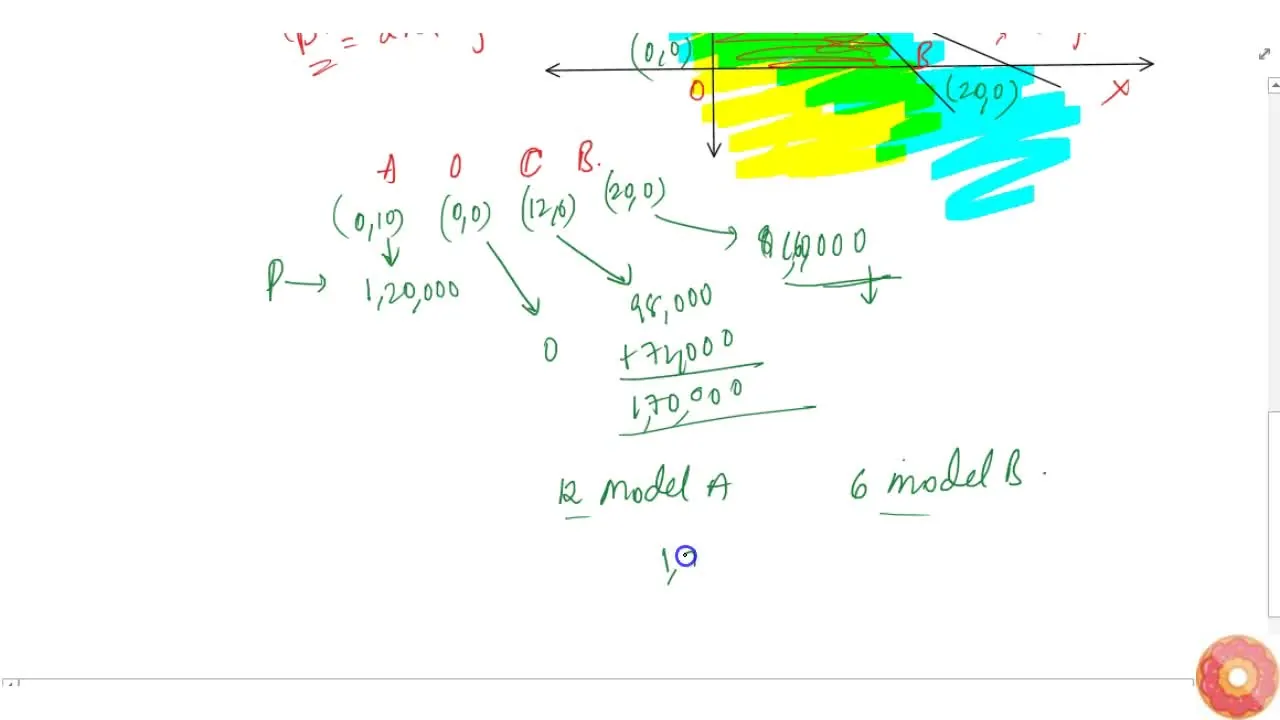
The feasible region (shaded) OABC determined by the linear inequalities (2) to
(4) is shown in Fig. Note that the feasible region is bounded.

Let us evaluate the objective function Z at each corner point as shown below:


Corner Point ----Z=8000
x+12000 y

0(0,0)----0

A(200)----160000

B(12,6)----168000 <--Maximum

C(0,10)----120000


We find that maximum value of Z is `1,68,000` at B`(12,6)`. Hence, the company should produce 12 pieces of Model A and 6 pieces of Model B to realise maximum profit and maximum profit then will be Rs. `1,68,000`.