Consider that an idela gas (n mole) is espanding in a process gives by p=f(v), which passes throught a point (V0,p0). Shown that the gas is absorbing heat at (p0,v0) if the slope of the curve p=f(v) is large than the slope of the adabatic passing throught (p0,v0).
According to question , slope of the curve = f(V) where V is volume.
∴ Slpoe of p = f(v) curve at (V0,p0) = f(v)
Slope of addiabtic at (V0,p0) = k(−γ)v1−γ−10=−γp0/v0
Now heat absorbed in the process p=f(v)
dQ=dU+dW=nC(v)dT+pdV ......(i)
∵ pV=nRT⇒T=(1nR)pV
⇒ T=(1nR)Vf(V)
⇒ dT=(1nR)[f(v)+Vf(V)]dV .........(ii)
Now from Eq. (i) dQdV=nCvdTdV+pdVdV=nCVdTdV+p
=nCVnR×[f(V)+Vf'(V)]+p [from Eq. (ii)]
=CVR[f(V)+Vf'(V)]+f(V) [∵p=f(V)]
⇒ [dQdV]V=V0=CVR[f(V0)+V0f'](V0)]+f(V0) ltBrgt =f(V0)[CVR+1]+V0f'(V0)CVR
∵ CV=Rγ−1⇒CVR=1γ−1
⇒ [dQdv]V=V0=[1γ−1+1]f(V0)+V0f'(V0)γ−1
γγ−1p0+V0γ−1f'(V0)
Heat is absorbed where dQdV>0, when gas expands
Hence, γp0+V0f'(V0)>0orf'(V0)>(−γpoVo)
Topper's Solved these Questions
- THERMODYNAMICS BOOK - NCERT EXEMPLARCHAPTER - THERMODYNAMICS EXERCISE - SHORT ANSWER TYPE QUESTIONS
6 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NCERT EXEMPLARCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Very short Answer type Questions
15 Videos
- UNITS AND MEASUREMENTS BOOK - NCERT EXEMPLARCHAPTER - UNITS AND MEASUREMENTS EXERCISE - Long Answer Type Questions
9 Videos
Similar Questions
Consider that an ideal gas (nmoles) is expanding in a process given by P=f(V), which passes through a point (P0,V0). Show that the gas is absorbing heat at (P0,V0) if the slope of the curve P=f(V) is larger than the slope of the adiabat passing through (p0,V0).
View Solutionn' moles of an ideal gas undergoes a process A→B as shown in the figure. The maximum temperature of the gas during the process will is p0v04nR then value of N is:
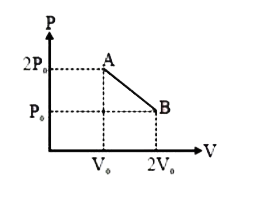
View Solution
Knowledge Check
One mole of a mono- atomic ideal gas undergoes a quasi- static process, which is depicted by a straight line joining points (V0T0) and (2V0,3T0) in a V - T diagram . What is the value of the heat capacity of the gas at the point (V0,T0) ?
ARB32RC2RD0The slope of P-V graph for isochoric process is
AZeroBInfiniteCOneDTwoOn P-V coordinates, the slope of an isothermal curve of a gas at a pressure P = IMPa and volume V= 0.0025 m3 is equal to −400Mpa/m3. If Cp/Cv=1.4 , the slope of the adiabatic curve passing through this point is :
A−56Mpa/m3B−400Mpa/m3C−560Mpa/m3DNone of these
Show that the entropy of a perfect gas can be written as S=CvInp+CpInV+S0 where S0 is a constant.
View SolutionIn process T∝1V, pressure of the gas increases from p0 to 4p0. Match the following.
View SolutionFor an ideal gas the slope of V-T graph during an adiabatic process is (dV)/(dT) = -matap∮wherevolumeandtemperatureareV_(0)andT_(0).F∈dthevalueofC_(p) of the gas. It is given that m is a positive number.
View SolutionAn ideal monatomic gas is at P0,V0. It is taken to final volume 2V0 when pressure is P0/2 in a process which is straight line on P−V diagram. Then
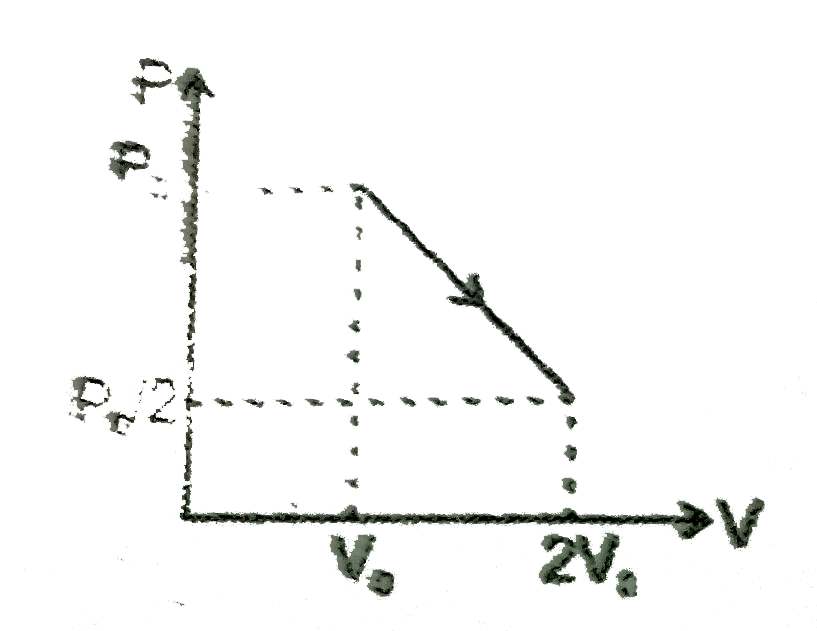
View SolutionOn P-V coordinates, the slope of an isothermal curve of a gas at a pressure P = IMPa and volume V= 0.0025 m3 is equal to −400Mpa/m3. If Cp/Cv=1.4 , the slope of the adiabatic curve passing through this point is :
View Solution
