Two stones are thrown vertically upwards simultaneously with their initial velocities u1andu2 respectively. Prove that the heights reached by them would be in the ratio of u21:u22 (Assume upward acceleration is −g and downward acceleration to be +g).
For lst stone,given initial velocity u = u1
Let height attained by it be h1
Form third equation of motion, v2=u2 - 2gh for upward motion
[Here, we have used nugative sigh, because as given upward acceleration is taken to be -q
At the highest point the velocity becomes zero i.e., v = 0
0=u21−2gh1
⇒2gh1=u21⇒h1=u212g
Similarly,
For llnd stone, given initial velocty, u = u2
Let the height attained by it be h2.
From third equation of motion, v2=u2−2gh
[at the highest point the velocity becomes zero i.e., v = 0]
0=u22−2gh2
∴2gh2=u22
⇒h2=u222g
Now , ratio of heights reached by the two stones
h1:h2=u212g:u222g
∴h1:h2=u21:u22 Hence proved
Topper's Solved these Questions
Similar Questions
Knowledge Check
Two bodies are thrown vertically upwards with their initial velocity in the ratio 2:3. Then the ratio of the maximum height attained by them is
A1:1B4:9C2:3D√2:√3A stone is thrown vertically upwards with an initial velocity u from the top of a tower of lieight 12u2g With what velocity does the stone reach the ground?
AuB4uC5uD2√6uA body thrown vertically upwards with an initial valocity u reaches maximum height in 6 s. The ratio of the distances traveled by the body in the first second the seventh second is
A1:1B11:1C1:2D1:11
A particle is thrown vertically upward with a velocity of u. Find its time of flight.
View SolutionA stone is thrown vertically upwards with an initial speed u from the top of a tower, reaches the ground with a speed 3u. The height of the tower is :
View SolutionQuestion Stimulus
A stone is thrown vertically upwards with an initial velocity of 30ms−1. Acceleration due to gravity g=10ms−2. The maximum height reached by the stone is
View SolutionTwo particles are thrown simultaneously from points A and B with velocities u1=2ms−1andu2−14ms−1, respectively, as shown in figure.
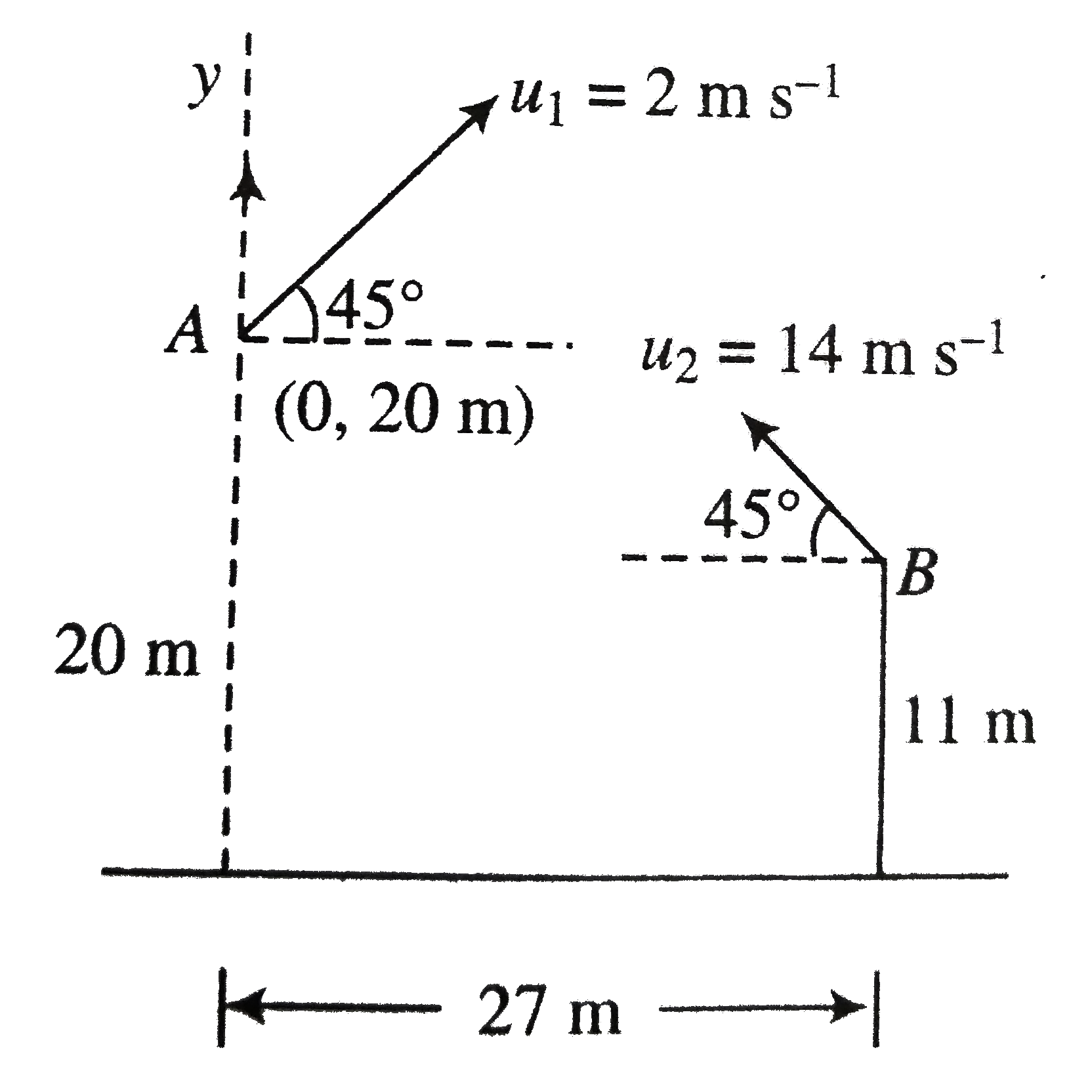
Minimum separation between A and B is
View SolutionTwo particles are thrown simultaneously from points A and B with velocities u1=2ms−1andu2−14ms−1, respectively, as shown in figure.
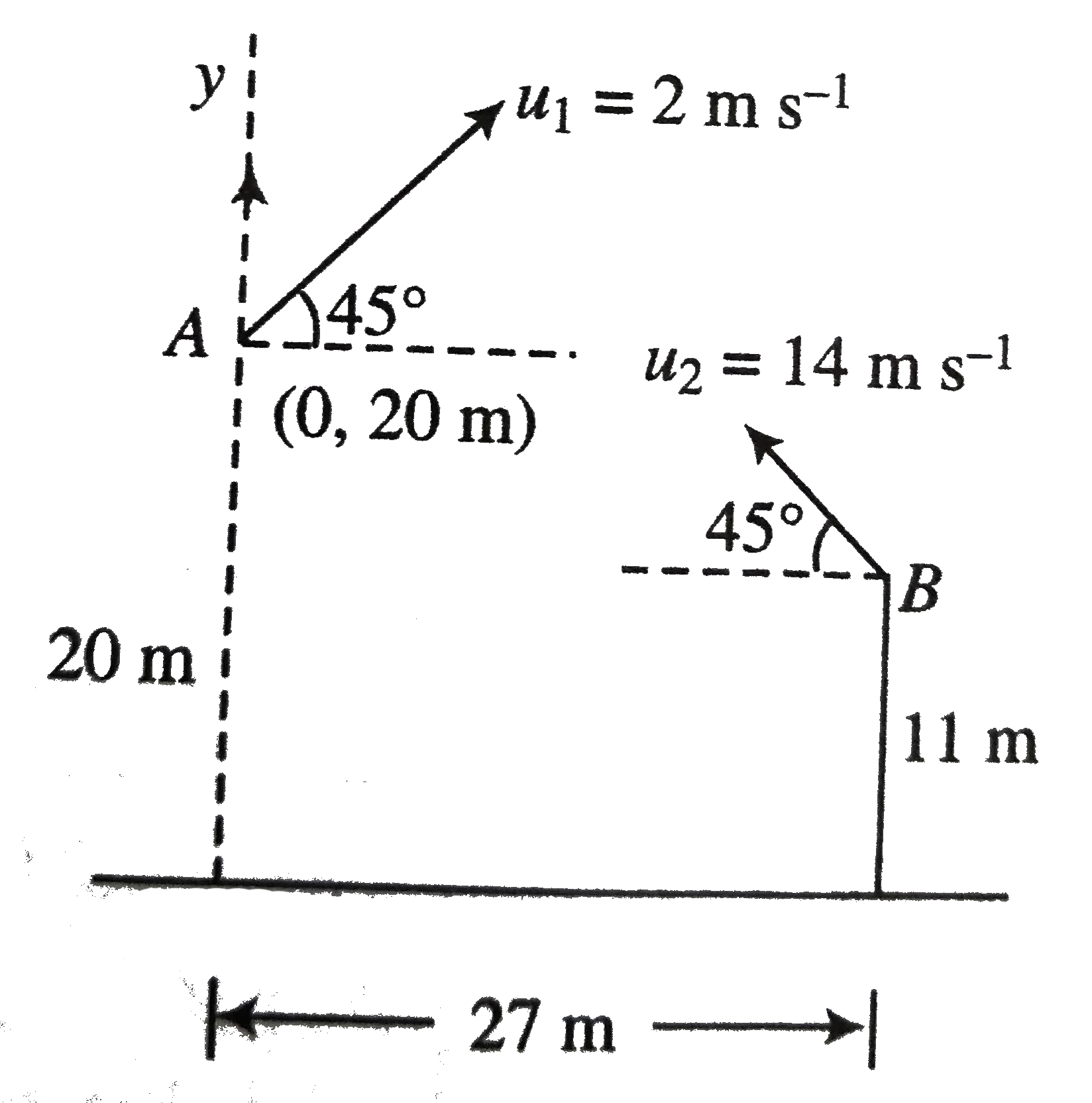
The relative velocity of B as seen from A in
View Solution