A car starts from rest and moves along the x-axis with constant acceleration 5ms−2 for 8 seconds. If it then continues with constant velocity, what distance will the car cover in 12 seconds since it started from the rest ?
Given, the car starts from rest so its initial velocity u = 0
Acceleration, (a)= 5ms−2 and time (t) = 8s
From first equation of motion,
v = u + at
On putting a = 5ms−2 and t = 8 s in above equation, we gel
v=0+5×8=40ms−1
So, final velocity v is 40ms−1 .
Again, from second equation of motion.
s = ut +12at2
On putting t = 8s and a = 5ms−2 in above equation we get
s=0×8+12×5×(8)2=12×5×64=5×32=160m
So, the distance covered in 8 s is 160m.
Given, total time t = 12s.
After 8s, the car continues with constant velocity i.e., the car will move with a velocity of 40ms−1
So, ramaining time t' = 12s−8s=4s
The distance covered in the last 4s(s) = Velocity × Time [∵ Distance = Velocity × Time]
= 40×4 = 160m
[We have used the direct formual because after 8s, car is moving with constant velocity i.e., zero acceleration]
∴ Total distance travelled in 12 s from the start
D = s+s=160+160=320m
Topper's Solved these Questions
Similar Questions
A car starts from rest and moves with uniform acceleration of 5 m/s2 for 8 sec. If the acceleration ceases after 8 seconds then find the distance covered in 12s starting from rest.
View SolutionA car starts from rest and moves with uniform acceleration of 5m/s^(2 for 8sec .If the acceleration ceases after 8seconds then find the distance covered in 12s starting from rest (in metres)
View Solution
Knowledge Check
A particle starts from rest and moves with constant acceleration. Then velocity displacement curve is:
A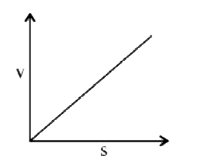 B
B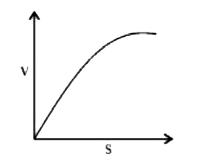 C
C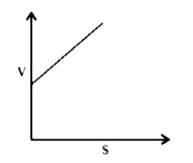 D
D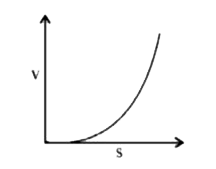
An object starts from rest at the origin and moves along the x axis with a constant acceleration of 4m/s2. Its average velocity as it goes from x=2 m to x=8 m is :
A2 m/sB3 m/sC5 m/sD6 m/sA car starts from rest and moves with constant acceleration. In first t seconds it covers distance x. Then distance covered by it in next t seconds will be:-
AxB2 xC3 xD4 x
A car starts from rest and moves with uniform acceleration of "5m/s^(2)for 8 sec.If theacceleration ceases after 8 seconds then find the distance covered in 12 s starting from rest (in metres)
View SolutionA body starts from rest and moves with a uniform acceleration of 10ms−2 for 5 seconds. During the next 10 seconds it moves with uniform velocity. Find the total distance travelled by the body (Using graphical analysis).
View SolutionA car starts from rest and accelerates at a constant rate in a straight line. In the first second, the car covers a distance of 2.0 meters. How much additional distance will the car cover during the second second of its motion ?
View SolutionA body starts from rest and moves with constant acceleration. The ratio of distance covered by the body in nth second to that covered in n second is.
View SolutionA particle starting from rest moves along a straight line with constant acceleration for this velocity displacement graph will have the form-
View Solution
