Before the neutrino hypothesis the beta decay process was throught to be the transition.
n→p+¯e
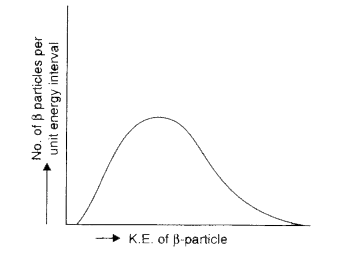
If this was true show that if the neutron was at rest the proton and electron would emerge with fixed energies and calculate them. Experimentally the electron energy was found to have a large range.
Before β−decay neutron is at rest Hence En=mnc2,pn=0
pn=pp+pe
or pp+pe=0⇒|pp|=|pe|=p
Also Ep=(m2pc4+p2pc2)12
Ep=(m2pc4+p2pc2)12
=(m2ec4+p2ec2)12
From conservation of energy
(m2pc2+p2c2)12+=(m2ec4+p2c2)12=mnc2
mpc2≈936MeV,mnc2≈938MeV,mec2=0.51MeV
since the energy difference between n and p is small pc will be small pc<<<mpc2 while pc may be breater than mec2
⇒ mpc2+p2c22m2pc4≈mnc2=pc
To first order pc≈mnc2−mpc2=938MeV−936MeV=2MeV
this gives the momentum of proton or neutron. then
Ep=(m2pc4+p2c2)12=√9362+22
≈936MeV
Ee=(m2ec4=p2c2)12=√(0.51)2+22
=2.06MeV
Topper's Solved these Questions
Similar Questions
Before the neutrino hypothesis the beta decay process was throught to be the transition.
n→p+¯e
If this was true show that if the neutron was at rest the proton and electron would emerge with fixed energies and calculate them. Experimentally the electron energy was found to have a large range.
View SolutionConsider the decay of a free neutron at rest: n⊤+e− Show that the tow-body dacay of this type must necessarily give an electron of fixed energy and, therefore, cannot for the observed continous energy distribution in the β-decay of a neutron or a nucleus.
View Solution
Knowledge Check
The β−decay process , discoverwd around 1900 , is basically the decay of a neutron (n) in the laboratory , a proton (p) and an electron (e¯) are observed as the decay that the kinetic energy of the electron should be a constant . But experimentally , if was observed that the electron kinectic energy has continuous spectrum Considering a three- body decay process , i.e.
n→p+e¯+¯νe, around 1930 , pauli expained the observed (¯νe) to be massaless and possessing negligible energy , and the neutrino to be at rest , momentum and energy conservation principle are applied from this calculate , the maximum kinectic energy of the electron is 0.8×106eV The kinectic energy carrect by the proton is only the recoil energy
If the - neutrono had a mass of 3eV/c2 (where c is the speed of light ) insend of zero mass , what should be the range of the kinectic energy K. of the electron ?A0≤k≤0.8×106eVB3.0eV≤k≤0.8×106eVC3.0eV≤k≤0.8×106eVD0≤k≤0.8×106eVThe β−decay process , discoverwd around 1900 , is basically the decay of a neutron (n) in the laboratory , a proton (p) and an electron (e¯) are observed as the decay that the kinetic energy of the electron should be a constant . But experimentally , if was observed that the electron kinectic energy has continuous spectrum Considering a three- body decay process , i.e.
n→p+e¯+¯νe, around 1930 , pauli expained the observed (¯νe) to be massaless and possessing negligible energy , and the neutrino to be at rest , momentum and energy conservation principle are applied from this calculate , the maximum kinectic energy of the electron is 0.8×106eV The kinectic energy carrect by the proton is only the recoil energy
What is the maximum energy of the anti-neutrino ?AzeroBMach less then 0.8×106eVCNearly 0.8×106eVDMach large then 0.8×106eVA metal foil is at a certain distance from an isotropic point source that emits energy at the rate P. Let us assume the classical physics to be applicable. The incident light energy will be absorbed continuously and smoothly. The electrons present in the foil soak up the energy incident on them. For simplicity , we can assume that the energy incident on a circular path of the foil with radius 5×10−11m (about that of a typical atom ) is absorbed by a single electron. The electron absorbs sufficient energy to break through the binding forces and comes out from the foil. By knowing the work function, we can calculate the time taken by an electron to come out i.e., we can find out the time taken by photoelectric emission to start. As you will see in the following questions, the time decay comes out to be large, which is not practically observed. The time lag is very small. Apparently, the electron does not have to soak up energy . It absorbs energy all at once in a single photon electron interaction.
If power of the source P is 1.5 W and distance of the foil from the source is 3.5 m, the energy received by an electron per second isA7.65×10−23 WB7.65×10−28 WC7.65×10−15 WD7.65×10−10 W
Consider the decay of a free neutron at rest: n⊤+e− Show that the tow-body dacay of this type must necessarily give an electron of fixed energy and, therefore, cannot for the observed continous energy distribution in the β-decay of a neutron or a nucleus.

View SolutionFollowing reactions are known as inverse beta decay
p+→v→n+e+
n+v→p+e−
These reactions have extremely low probabilities. Because of this, neutrinos and antineutrinos are able to pass through vast amount of matter without any interaction. In an experiment to detect neutrinos, large number of neutrinos coming out from beta decays of a radioactive material were made to pass through a tank of water, containing a cadmium compound in solution, which provided the protons to interact with antineutrinos, which provided the protons to interact with antineutrinos. Immediately after a proton absorbed a neutrino to yield a positron and a neutron, the positron encountered an electron and both got annihilated. the gamma ray detectors surrounding the tanks responded to the resulting photons. This confirmed that the above reaction has taken place.
(a) How many gamma ray photons are produced when a electron annihilates with a positron? What is energy of each photon? Take the mass of an electron to be 0.00055 u.
(b) The neutron produced in the above reaction was captured by .112Cd to form .113Cd. The atomic masses of these two isotopes of cadmium are are 111.9028u and 112.9044u respectively. mass of a neutron is 1.0087u. find the Q value of this reaction. Assume half of this energy is excitation energ of .113Cd. if the nucleus de-excites by emitting a gamma ray photon find its wavelenght.
View SolutionRead the pasage given below as well as the adjoining energy level diagram and then answer the questions given after the passage .
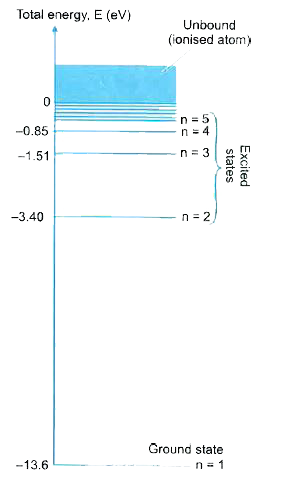
As per Bohr's theory og hydrogen atom the energy of an atom in a state corresponding to principal quantum number n is given as :
En=−13.6n2eV
The energy of an atom is the least when its electron is revolving in an orbit closets to the nucleus i.e., the one for which n =1. This state is called the ground state. When a hydrogen atom receives energy by processes such as electron collision , the atom may acquire sufficient energy to raise the electron to higher energy states and the atom is then said to be in an excited state . From these excited states the electron can then fall back to a state of lower energy , emitting a photon in the process.
The energy level diagram for the stationary states of a hydrogen atom , compouted from Bohr's relation for energy , is given in Fig.12.02. The principal quantum number n labels the stationary states in the ascending order of energy . Obviously , the highest energy corresponds to n=∞ and has an energy of 0 eV. This is the energy of the atom when the electron is completely removed (r=∞) from the nucleus and is at rest.
Now answer the follwoing questions:
Which atomic transition correspond to spectral lines of hydrogen in visible light ?
View SolutionRead the pasage given below as well as the adjoining energy level diagram and then answer the questions given after the passage .
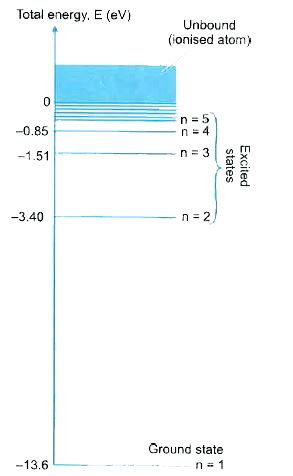
As per Bohr's theory og hydrogen atom the energy of an atom in a state corresponding to principal quantum number n is given as :
En=−13.6n2eV
The energy of an atom is the least when its electron is revolving in an orbit closets to the nucleus i.e., the one for which n =1. This state is called the ground state. When a hydrogen atom receives energy by processes such as electron collision , the atom may acquire sufficient energy to raise the electron to higher energy states and the atom is then said to be in an excited state . From these excited states the electron can then fall back to a state of lower energy , emitting a photon in the process.
The energy level diagram for the stationary states of a hydrogen atom , compouted from Bohr's relation for energy , is given in Fig.12.02. The principal quantum number n labels the stationary states in the ascending order of energy . Obviously , the highest energy corresponds to n=∞ and has an energy of 0 eV. This is the energy of the atom when the electron is completely removed (r=∞) from the nucleus and is at rest.
Now answer the follwoing questions:
Calculate the wavelenght of first spectral lines of series mentioned in part (g) of question.
View SolutionA metal foil is at a certain distance from an isotropic point source that emits energy at the rate P. Let us assume the classical physics to be applicable. The incident light energy will be absorbed continuously and smoothly. The electrons present in the foil soak up the energy incident on them. For simplicity , we can assume that the energy incident on a circular path of the foil with radius 5×10−11m (about that of a typical atom ) is absorbed by a single electron. The electron absorbs sufficient energy to break through the binding forces and comes out from the foil. By knowing the work function, we can calculate the time taken by an electron to come out i.e., we can find out the time taken by photoelectric emission to start. As you will see in the following questions, the time decay comes out to be large, which is not practically observed. The time lag is very small. Apparently, the electron does not have to soak up energy . It absorbs energy all at once in a single photon electron interaction.
if work function of the metal of the foil is 2.2 eV, the time taken by electron to come out is nearly
View Solution

