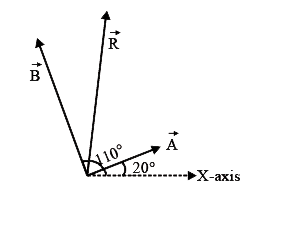
A vector →A and →B make angles of 20∘ and 110∘ respectively with the X-axis. The magnitudes of these vectors are 5m and 12m respectively. Find their resultant vector.
The correct Answer is:125
Angle between the →Aand→B=110∘−20∘=90∘
R=√A2+B2+2ABcos90∘=√52+122=13m
Let angle of →R from →A is α
tanα=BsinθA+Bcosθ=12sin90∘5+12cos90∘=12×15+12×0=125
orα=tan−1(125) with vector →A or (α+20∘) with X-axis
Similar Questions
Knowledge Check
- Question 1 - Select One
A vector a makes 30∘ and b makes 120∘ angle with the x-axis. The magnitude of these vectors are 3 unit and 4 unit, respectively. The magnitude of resultant vector is
A3 unitB4 unitC5 unitD1 unit - Question 2 - Select One
The resultant of →a and →b makes α with →a and β with →b, then (a,b represent magnitudes of respective vectors) :
Aα<βBα<βifa<bCα<βifa>bDα<βifa=b - Question 3 - Select One
Two vectors →Pand→Q are inclinded to each other at 60∘. The magnitude of →Pand→Q are 10 and 15 units respectively. What is the angle (α) made by their resultant →R with →P ?
Aα=tan−1(0.5)Bα=tan−1(0.6134)Cα=tan−1(0.7422)Dα=tan−1(0.92)
If a vector →A makes angles 45∘ and 60∘ with x and y axis respectively, then the angle made by it with z- axis is x×10∘ find x
View SolutionA vector →A of length 10 units makes an angle of 60∘ with a vector →B of length 6 units. Find the magnitude of the vector difference →A−→B & the angles with vector →A.
View SolutionIf →i and →j are unit vectors along x-axis and y-axis respectively, the magnitude of vector →i+→j will be :-
View SolutionThe magnitude of x and y components of →A are 7 and 6 respectively . Also , the magnitudes of x and y components of →A+→B are 11 and 9 respectively . Calculate the magnitude of vector →B
View SolutionThe x and y components of vectors →A are 4 m and 6 m respectively. The x and y components of vector (→A+→B) are 12 m and 10 m respectively. Then what are the x and y component . of vector →B ?
View Solution
