How many peaks (humps) will be noticed in the radial probability graph of the 4s orbital?
To determine how many peaks (humps) will be noticed in the radial probability graph of the 4s orbital, we can follow these steps:
1. Identify the Principal Quantum Number (n):
- The principal quantum number for the 4s orbital is n=4.
2. Determine the Azimuthal Quantum Number (l):
- For s orbitals, the azimuthal quantum number l=0.
3. Calculate the Number of Radial Nodes:
- The formula for calculating the number of radial nodes is given by:
Radial Nodes=n−l−1
- Substituting the values:
Radial Nodes=4−0−1=3
4. Relate Radial Nodes to Peaks (Humps):
- The number of peaks (humps) in the radial probability distribution graph is equal to the number of radial nodes plus one:
Number of Peaks=Radial Nodes+1
- Therefore:
Number of Peaks=3+1=4
5. Conclusion:
- The radial probability graph of the 4s orbital will show 4 peaks (humps).
Final Answer:
The number of peaks (humps) in the radial probability graph of the 4s orbital is 4.
---
- The principal quantum number for the 4s orbital is n=4.
- For s orbitals, the azimuthal quantum number l=0.
- The formula for calculating the number of radial nodes is given by:
Radial Nodes=n−l−1
- Substituting the values:
Radial Nodes=4−0−1=3
- The number of peaks (humps) in the radial probability distribution graph is equal to the number of radial nodes plus one:
Number of Peaks=Radial Nodes+1
- Therefore:
Number of Peaks=3+1=4
- The radial probability graph of the 4s orbital will show 4 peaks (humps).
The number of peaks (humps) in the radial probability graph of the 4s orbital is 4.
Similar Questions
Knowledge Check
There are two nodes in the radial probability distribution curve for the orbital with
An=2,n=0Bn=3,l=1Cn=4,l=3Dn=3,l=0Which of the following radial probability distribution graph is correct for 5s orbital ?
A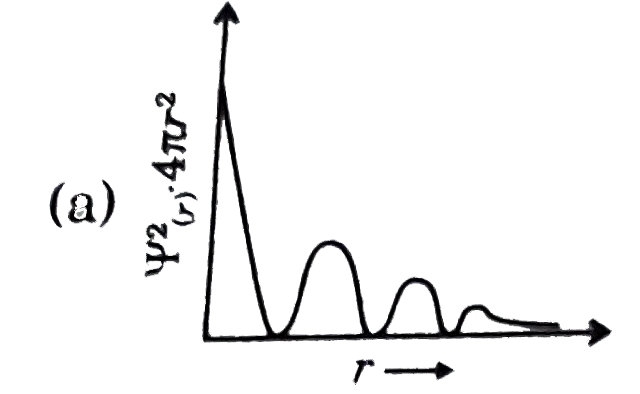 B
B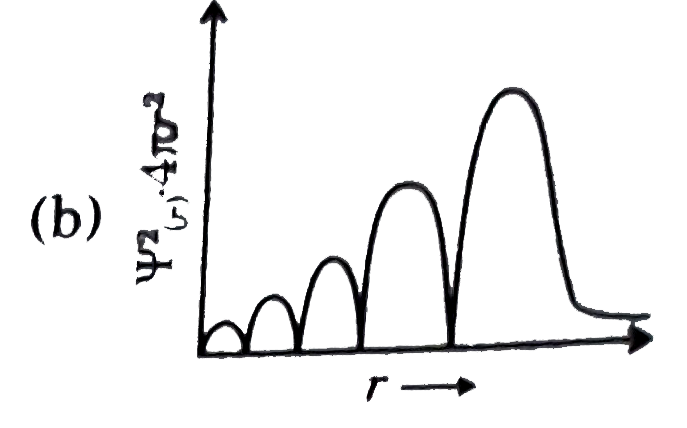 C
C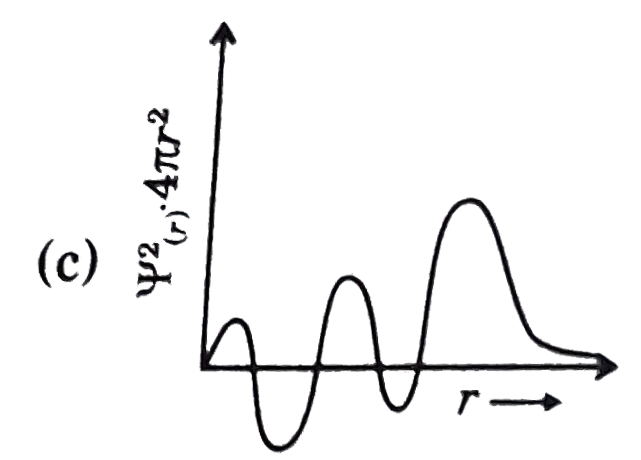 D
D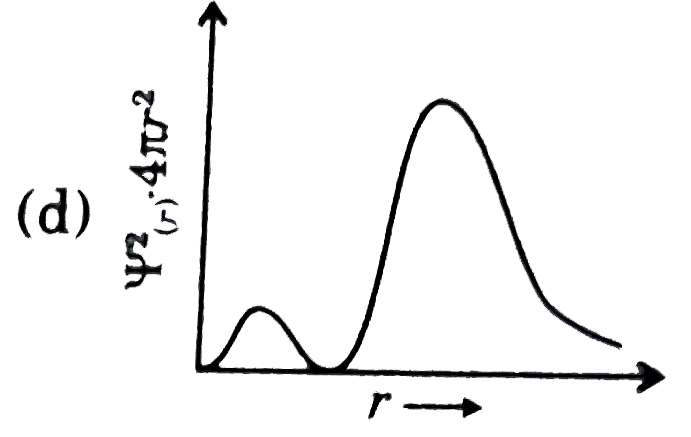
How many peacks are present in the radial distribution function for the 3d orbital?
AZeroBOneCTwoDThree
How many radial/spherical nodes will be present in the 5f orbital ?
View SolutionHow many electrons can be accommodated in the s-orbital?
View SolutionOut of the following, which is the correct match for the radial probability of finding the electron for 2s orbital
View SolutionWhich of the following graph is correct for 2s orbital?
View SolutionHow many humps does a Llama have?
View Solution

