If an electron drops from n = 4 to n = 2 in then would the released wavelength lie in the visible region?
To determine whether the wavelength released when an electron drops from n = 4 to n = 2 in Li²⁺ lies in the visible region, we can follow these steps:
Step 1: Identify the transition
The electron is transitioning from a higher energy level (n = 4) to a lower energy level (n = 2).
Step 2: Use the Rydberg formula
We will use the Rydberg formula for hydrogen-like atoms to calculate the wavelength of the emitted photon:
1λ=RZ2(1n21−1n22)
where:
- R is the Rydberg constant (approximately 109678cm−1),
- Z is the atomic number (for Li, Z=3),
- n1 is the lower energy level (2),
- n2 is the higher energy level (4).
Step 3: Substitute the values into the formula
Substituting the values into the formula:
1λ=109678cm−1×32(122−142)
Calculating Z2:
Z2=32=9
Calculating the fractions:
122=14,142=116
Now, calculating the difference:
14−116=416−116=316
Now substituting back into the equation:
1λ=109678×9×316
Step 4: Calculate 1λ
Calculating the value:
1λ=109678×9×316=185081cm−1
Step 5: Calculate λ
To find λ:
λ=1185081cm−1
Converting λ to meters:
λ=1185081×100m=5.403×10−8m
Step 6: Convert to Angstroms
To convert meters to Angstroms (1 Angstrom = 10−10 m):
λ=5.403×10−8m=540.3Angstroms
Step 7: Determine if it lies in the visible range
The visible light range is approximately 4000 to 7500 Angstroms. Since 540.3 Angstroms is within this range, we conclude that the wavelength released does lie in the visible region.
Conclusion
The wavelength released when an electron drops from n = 4 to n = 2 in Li²⁺ is approximately 540.3 Angstroms, which is in the visible region.
---
The electron is transitioning from a higher energy level (n = 4) to a lower energy level (n = 2).
We will use the Rydberg formula for hydrogen-like atoms to calculate the wavelength of the emitted photon:
1λ=RZ2(1n21−1n22)
where:
- R is the Rydberg constant (approximately 109678cm−1),
- Z is the atomic number (for Li, Z=3),
- n1 is the lower energy level (2),
- n2 is the higher energy level (4).
Substituting the values into the formula:
1λ=109678cm−1×32(122−142)
Calculating Z2:
Z2=32=9
Calculating the fractions:
122=14,142=116
Now, calculating the difference:
14−116=416−116=316
Now substituting back into the equation:
1λ=109678×9×316
Calculating the value:
1λ=109678×9×316=185081cm−1
To find λ:
λ=1185081cm−1
Converting λ to meters:
λ=1185081×100m=5.403×10−8m
To convert meters to Angstroms (1 Angstrom = 10−10 m):
λ=5.403×10−8m=540.3Angstroms
The visible light range is approximately 4000 to 7500 Angstroms. Since 540.3 Angstroms is within this range, we conclude that the wavelength released does lie in the visible region.
The wavelength released when an electron drops from n = 4 to n = 2 in Li²⁺ is approximately 540.3 Angstroms, which is in the visible region.
Similar Questions
Calculate the longest wavelengths belonging to Lyman and Balmer series. Which of these wavelengths will lie in the visible region ?
View SolutionAn electron in a hydrogen atom is excited from the ground state to the n = 4 state. Predict which of the following statements are true or false :
(i) n=4 is the first excited state.
(ii) It takes more energy to ionize (remove) the electron from n = 14 than in the ground state.
(iii) The wavelength of light emitted when the electron drops from n=4 to n=2 is longer than that from n=4 to n=1.
(iv) The wavelength which the atom absorbs in going from n=1 to n=4 is the same as emitted when it goes from n=4 to n=1.
(v) The electron is farther from the nucleus (on average) in n = 4 than in the ground state.
View Solution
Knowledge Check
If an electron of a hydrogen atom jumps from n=2 to n=1 then find the wavelength of released photon
A121.5nmB123.15nmC125.15nmD128.15nmIf an electron undergoes transition from n = 2 to n =1 in Li2+ ion , the energy of photon radiated will be best given by
AhvBhv1+hv2Chv1+hv2+hv3DAll of theseIn a set of experiment on a hydrogen on a hypothetical one-electron atom, the wavelength of the photons emitted from transition ending in the ground state (n=1) are shown in the energy level diagram
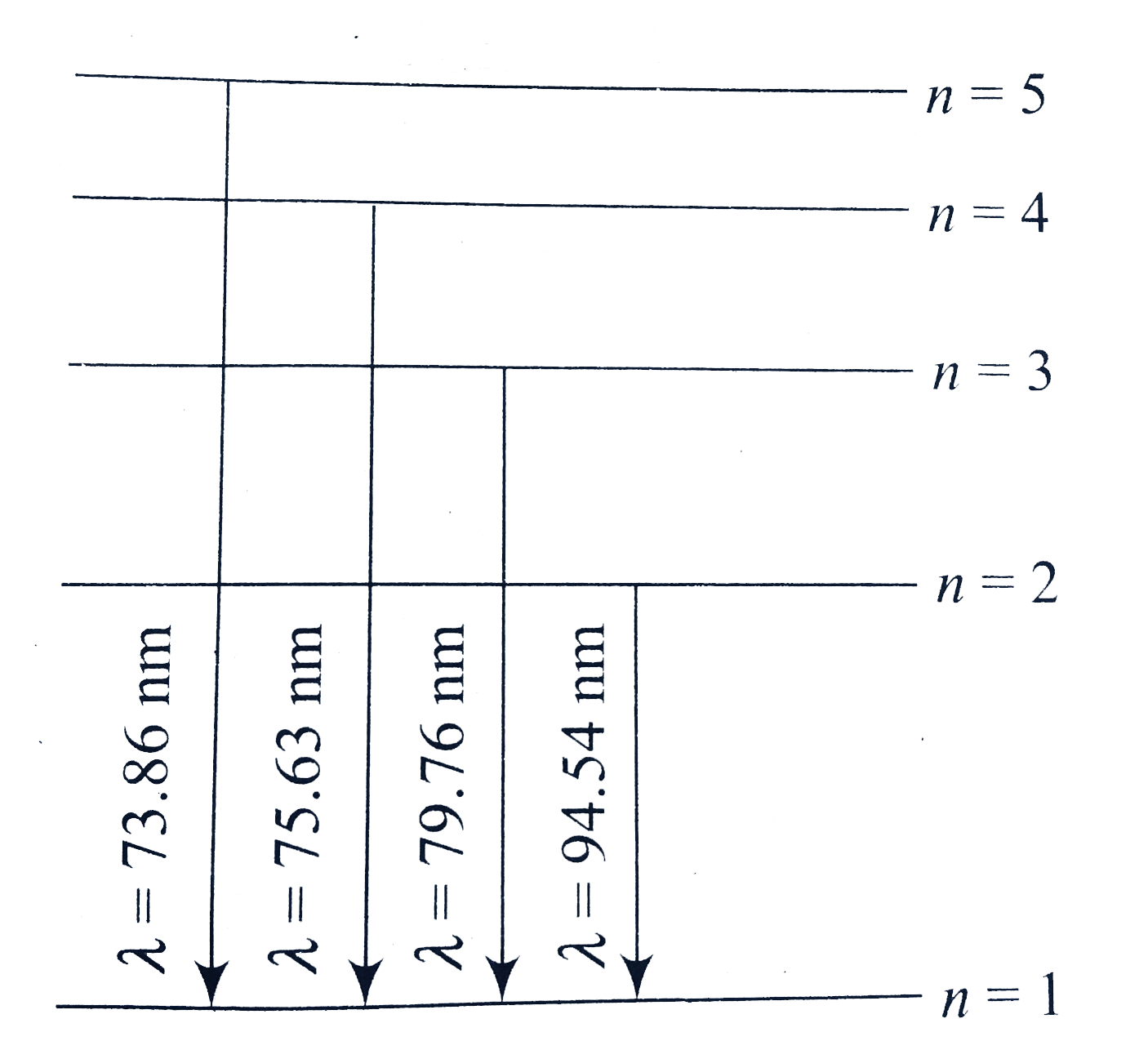
λ5→1=73.86nm
λ4→1=75.63nm
λ3→1=79.76nm
λ2→1=94.54nm
If an electron made a transition from n = 4 to n = 2 level, the wavelength of the light that it would emit is nearlyA380nmB190nmC76nmD510nm
if electron falls from n=3 to n=2, then emitted energy is
View SolutionThe range of wavelength of the visible light is
View SolutionIn excited H atom when electron drop from n=4,5,6 to n=1, there is emission of
View SolutionA photon of wavelength 6.2 nm is used to emit an electron from the ground state of Li2+ . Calculate de Broglie wavelength of the emitted electron .
View SolutionThe atomic spectrum of Li+2 ion arises due to the transition of an electron from n2 to n1 if n1+n2=4 and (n2−n1) =2 then the wavelength of 3rd line of this series in Li+2 ion will be
View Solution