Verhulst - Pearl Logistic growth equation is :
dNdt=rN
dNdt=rN[K−Nk]
Nt=N0ert
(b - d)
The correct Answer is:B
Step-by-Step Solution:
1. Understanding Population Growth Models:
- There are two primary models of population growth: Exponential Growth and Logistic Growth.
- Exponential growth occurs when resources are unlimited, leading to a J-shaped curve.
- Logistic growth occurs when resources are limited, resulting in an S-shaped curve.
2. Identifying the Logistic Growth Equation:
- The logistic growth model accounts for the carrying capacity of the environment, denoted by 'k'.
- The carrying capacity is the maximum population size that an environment can sustain.
3. Deriving the Logistic Growth Equation:
- The logistic growth equation is derived from the change in population density over time (dn/dt).
- The equation is given by:
dndt=r⋅n(k−nk)
- Here:
- n = population density
- r = intrinsic growth rate
- k = carrying capacity
4. Interpreting the Equation:
- The term (k−n)/k represents the fraction of the carrying capacity that is still available for growth.
- As the population n approaches the carrying capacity k, the growth rate dn/dt decreases, leading to stabilization of the population.
5. Conclusion:
- The correct logistic growth equation is:
dndt=r⋅n(k−nk)
- This reflects how population growth slows as resources become limited.
- There are two primary models of population growth: Exponential Growth and Logistic Growth.
- Exponential growth occurs when resources are unlimited, leading to a J-shaped curve.
- Logistic growth occurs when resources are limited, resulting in an S-shaped curve.
- The logistic growth model accounts for the carrying capacity of the environment, denoted by 'k'.
- The carrying capacity is the maximum population size that an environment can sustain.
- The logistic growth equation is derived from the change in population density over time (dn/dt).
- The equation is given by:
dndt=r⋅n(k−nk)
- Here:
- n = population density
- r = intrinsic growth rate
- k = carrying capacity
- The term (k−n)/k represents the fraction of the carrying capacity that is still available for growth.
- As the population n approaches the carrying capacity k, the growth rate dn/dt decreases, leading to stabilization of the population.
- The correct logistic growth equation is:
dndt=r⋅n(k−nk)
- This reflects how population growth slows as resources become limited.
Similar Questions
Knowledge Check
Verhult - Pearl logistic growth pattern is :-
ASigmoidBParabolaCHyperbolaDJ-shapedWhich of the following curve represents Verhulst Pearl Logistic growth in a populations ?
A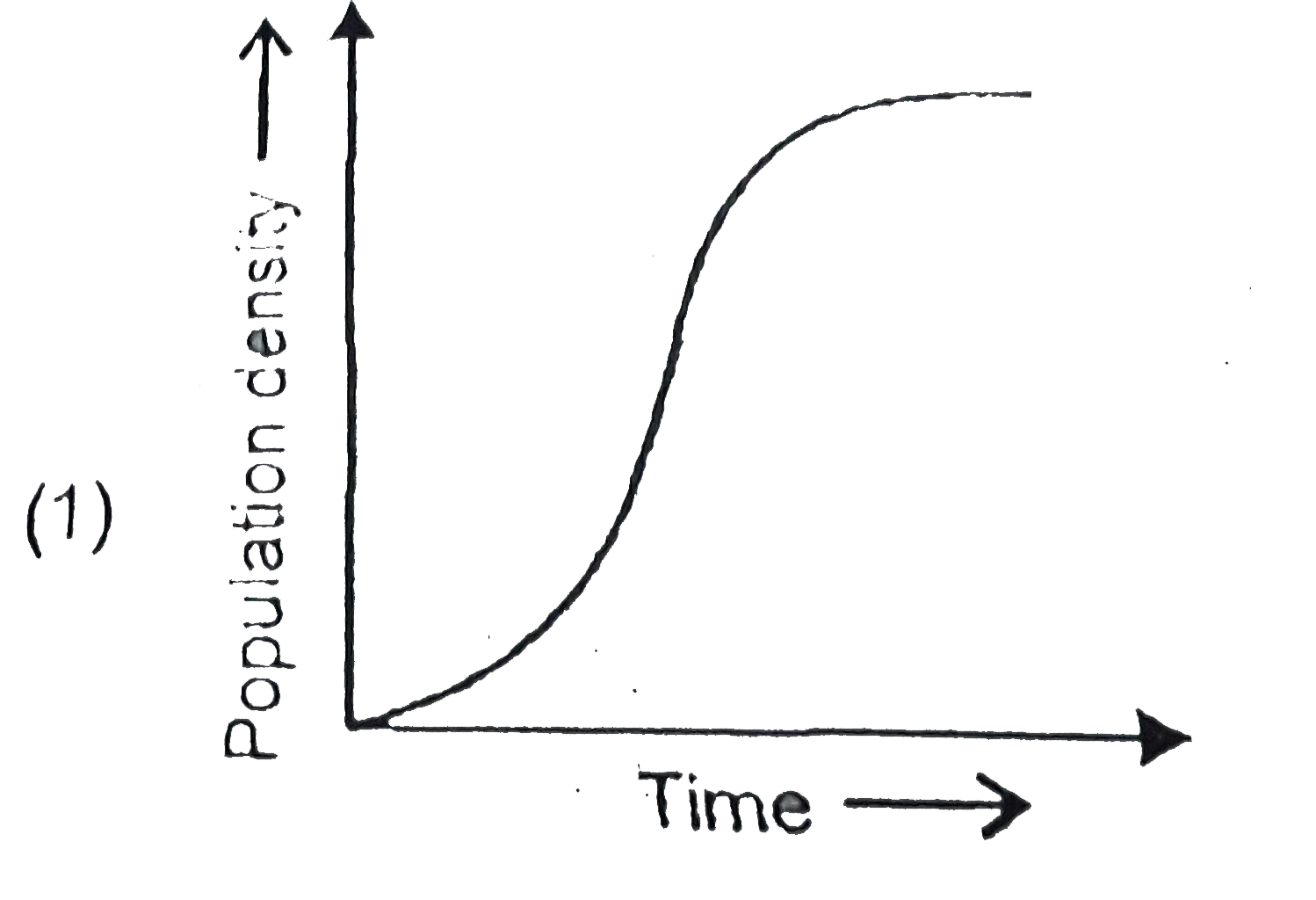 B
B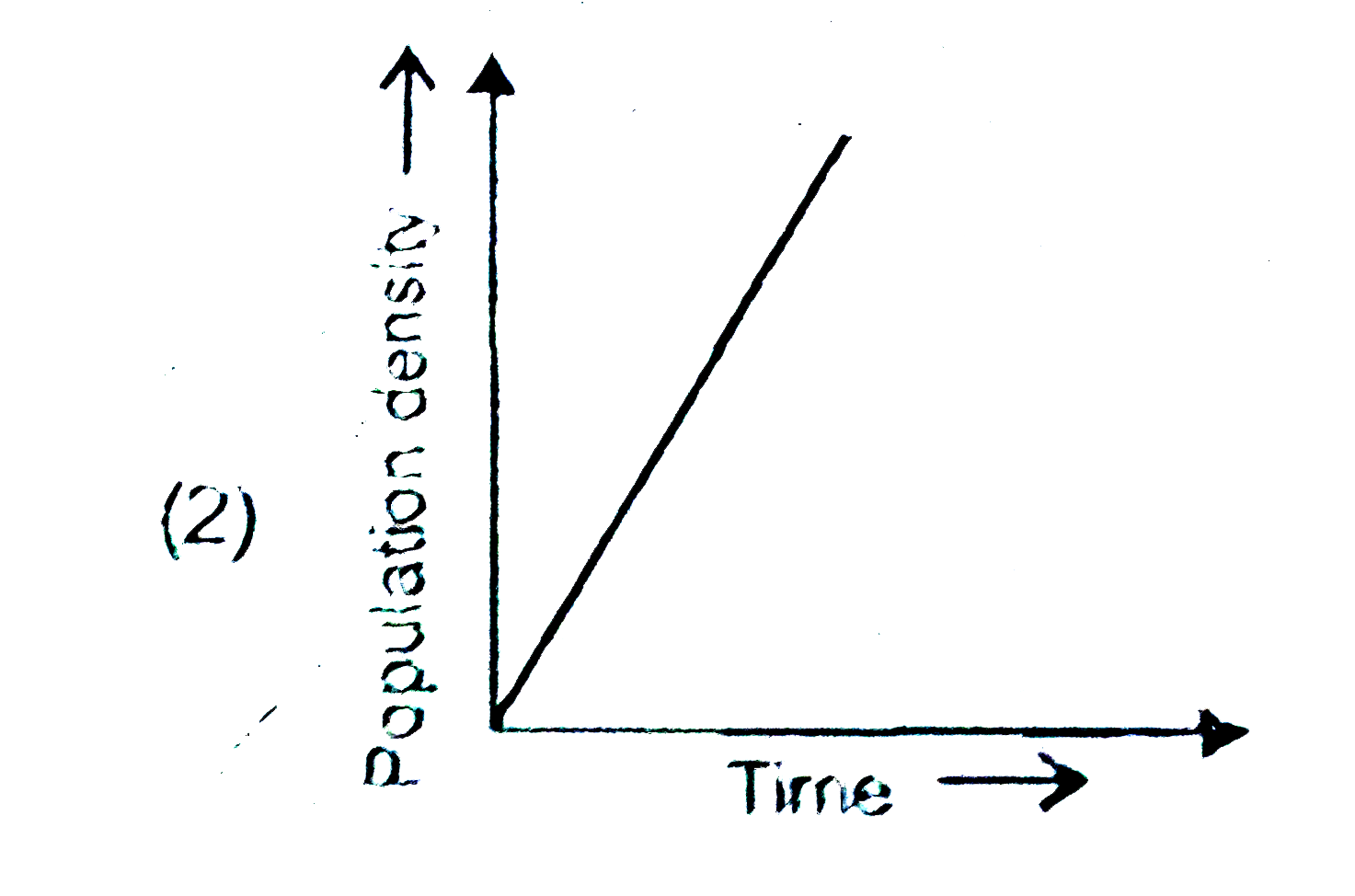 C
C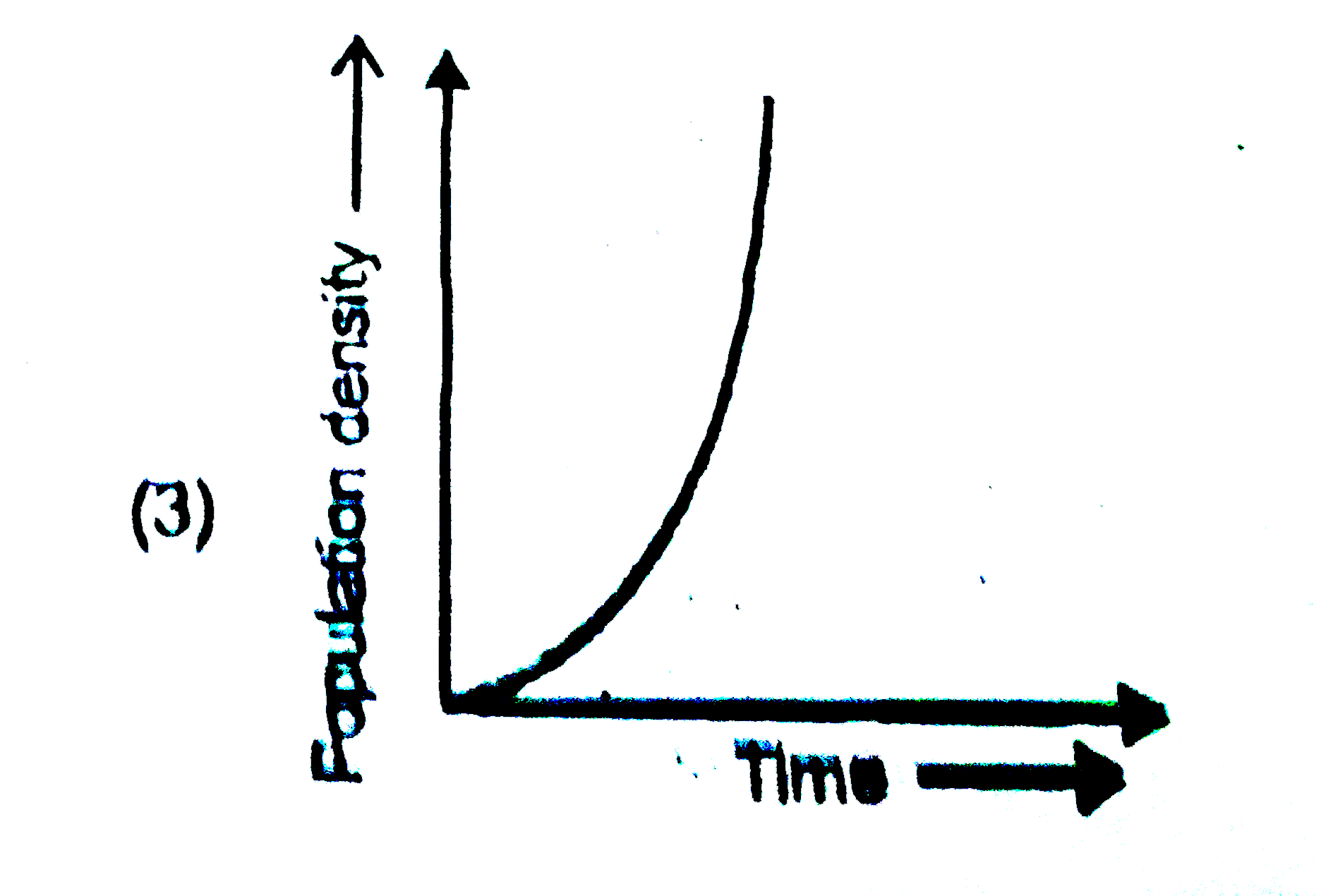 D
D
Verhulst-pearl logistic growth patten is
AsigmoidBj-shapedCstraight lineDhyperbola
Explain the principle of carrying capacity by using population Verhulst-Pearl logistic growth curve.
View SolutionVerhulst-pearl logistic growth patten is
View SolutionThe Verhulst-Pearl logistic growth is described to the equation dNdt=rNK−NK, in this K stand
View SolutionThe Verhulst-Pearl logistic growth is described to the equation dNdt=rNK−NK, in this K stand
View Solutionwhich of the following option is true for verhulst Pearl logistic growth?
(A)population growth is decreased by the equation dNdt=rN[KK−N].
(B) r' represents biotic potential.
(C) applicable to a population growing in habitat with limited resources.
(D)K represents carrying capacity
View Solution
