For balmer series in the spectrum of atomic hydrogen the wave number of each line is given by
where is a constant and and are integers which of the following statement (S) is / are correct
1 as wavelength decreases the lines in the series converge
2 The integer is equal to 2
3 The ionization energy of hydrogen can be calculated from the wave number of these lines
4 The line of longest wavelength corresponds to
1,2 and 3
2,3 and 4
1,2 and 4
2 and 4 only
The correct Answer is:C
To solve the question regarding the Balmer series in the spectrum of atomic hydrogen, we will analyze each statement provided in the question step by step.
Given:
The wave number of each line in the Balmer series is given by:
¯V=RH(1n21−1n22)
where RH is a constant, and n1 and n2 are integers.
Analyzing Each Statement:
1. Statement 1: As wavelength decreases, the lines in the series converge.
- Explanation: In the context of wave numbers, as the wavelength decreases, the wave number ¯V increases. For the Balmer series, n1 is fixed at 2, while n2 can take values 3, 4, 5, etc. As n2 increases, the difference (1n21−1n22) becomes smaller, leading to convergence of the lines. Thus, this statement is True.
2. Statement 2: The integer n1 is equal to 2.
- Explanation: In the Balmer series, transitions occur from higher energy levels n2 (3, 4, 5, ...) to n1=2. Therefore, this statement is True.
3. Statement 3: The ionization energy of hydrogen can be calculated from the wave number of these lines.
- Explanation: The ionization energy refers to the energy required to remove an electron completely from the atom. The Balmer series only involves transitions where n1=2 and n2 is greater than 2. To calculate ionization energy, we would need to consider transitions from n=1 to n=∞. Therefore, this statement is False.
4. Statement 4: The line of longest wavelength corresponds to n2=3.
- Explanation: The longest wavelength corresponds to the smallest energy transition, which occurs when n2 is at its minimum value. For the Balmer series, the transition from n2=3 to n1=2 gives the longest wavelength. Therefore, this statement is True.
Conclusion:
Based on the analysis:
- Statement 1: True
- Statement 2: True
- Statement 3: False
- Statement 4: True
Thus, the correct statements are 1, 2, and 4.
Final Answer:
The correct option is 1, 2, and 4.
---
The wave number of each line in the Balmer series is given by:
¯V=RH(1n21−1n22)
where RH is a constant, and n1 and n2 are integers.
- Explanation: In the context of wave numbers, as the wavelength decreases, the wave number ¯V increases. For the Balmer series, n1 is fixed at 2, while n2 can take values 3, 4, 5, etc. As n2 increases, the difference (1n21−1n22) becomes smaller, leading to convergence of the lines. Thus, this statement is True.
- Explanation: In the Balmer series, transitions occur from higher energy levels n2 (3, 4, 5, ...) to n1=2. Therefore, this statement is True.
- Explanation: The ionization energy refers to the energy required to remove an electron completely from the atom. The Balmer series only involves transitions where n1=2 and n2 is greater than 2. To calculate ionization energy, we would need to consider transitions from n=1 to n=∞. Therefore, this statement is False.
- Explanation: The longest wavelength corresponds to the smallest energy transition, which occurs when n2 is at its minimum value. For the Balmer series, the transition from n2=3 to n1=2 gives the longest wavelength. Therefore, this statement is True.
Based on the analysis:
- Statement 1: True
- Statement 2: True
- Statement 3: False
- Statement 4: True
The correct option is 1, 2, and 4.
Similar Questions
Knowledge Check
For balmer series in the spectrum of atomic hydrogen the wave number of each line is given by ¯¯¯V=R[1n21−1n22] where RH is a constant and n1 and n2 are integers. Which of the following statements (s), is (are correct)
1. As wave length decreases the lines in the series converge
2. The integer n1 is equal to 2.
3. The ionisation energy of hydrogen can be calculated from the wave numbers of three lines.
4. The line of shortest wavelength corresponds to = 3.A1, 2 and 3B2, 3 and 4C1, 2 and 4D2 and 4 onlyFor Balmer series in the spectrum of atomic hydrogen, the wave number of each line is given by v=RII(1n21−1n22) where RII is a constant and n1andn2 are integers. Which of the following statement (s) is (are) correct ?
(i) As wavelength decreases, the lines in the series converge.
(ii) The interger n1 is equal to 2.
(iii) The ionization energy of hydrogen can be calculated from the wave number of these lines.
(iv) The line of longest wavelength corresponds to n2=3.A(i), (ii) and (iii)B(ii), (iii) and (iv)C(i), (ii) and (iv)D(ii) and (iv)In hydrogen spectrum wave number of different lines is given by 1λ=RH⎡⎣1n2i−1n2f⎤⎦ where RH=1.090678×107m−1 The wavelength of first line of Lyman series would be
A122×10−7mB9.1176×10−8mC12.2×10−7mD1.22×10−7m
For the Paschen series the values of n1 and n2 in the expression ΔE=RH.c(1n21−1n22)
View SolutionFor the Paschen series thr values of n1 and n2 in the expression ΔE=RHc[1n21−1n22] are
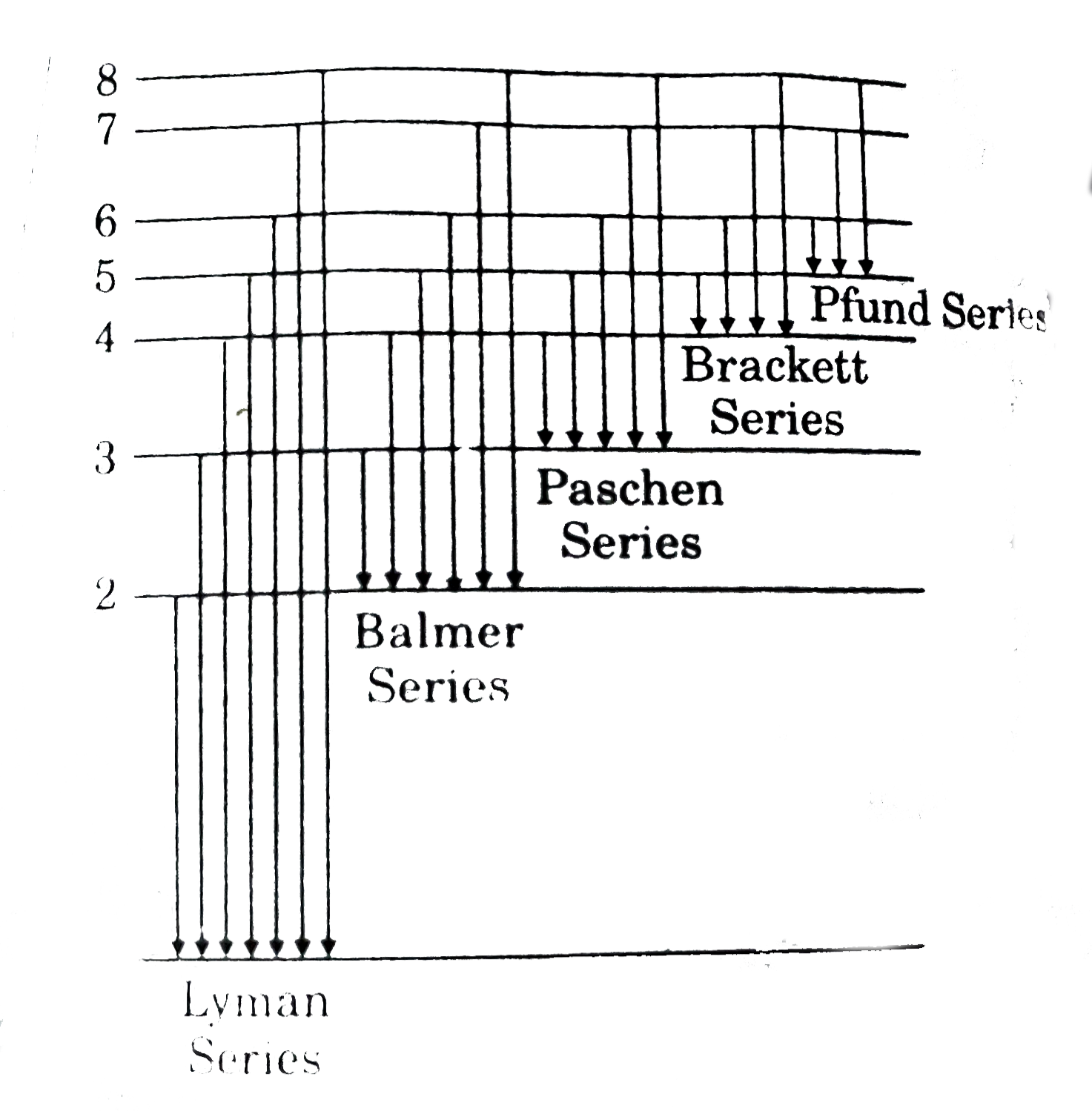
View Solutionthe only electron in the hydrogen atom resides under ordinary conditions in the first orbit. When energy is supplied the electron moves to higher energy orbit depending on the amount of energy absorbed. It emits energy. Lyman series is formed when the electron returns to the lowest orbit while Balmer series is formed when the electron returns to second. Similarly, Paschen, Breakett and Pfund series are formed when electron returns to the third, fourth and fifth orbits from higher energy orbits respectively (as shown in figure).

Maximum number of different lines produced when electron jump from nth level to ground level is equal to
n(n−1)2.
For example in the case of n=4, number of lines produced is 6.(4→3,4→2,4→1,3→2,3→1,2→1).When an electron returns from n2ton1 state, the number of different
lines in the spectrum will be equal to (n2−n1)(n2−n1+1)2
If the electron comes back from energy level having energy E2 to energy level having energy E1, then the difference may be expressed in terms of energy of photon as:
E2−E1=ΔE,λ=hcΔE,ΔE=hv(v−frequency)
Since h and c are constants ΔE corresponds to definite energy: thus each transition from one energy level to another will produce a light of definite wavelength. This is actually observed as a line in the spectrum of hydrogen atom.
Wave number of line is given by the formula:
¯v=RZ2(1n21−1n22)
where R is a Rydberg constant (R=1.1×107m−1).
(i) First line of a series : It is called line of longest wavelength of line of smallest energy'.
(ii) Series limit or last line of a series : It is the line of shortest wavelength or line of highest energy.
Last line of breakett series for H-atom has wavelength λ1Å and 2nd line of Lyman series has wavelength λ2Åthen:
View Solutionthe only electron in the hydrogen atom resides under ordinary conditions in the first orbit. When energy is supplied the electron moves to higher energy orbit depending on the amount of energy absorbed. It emits energy. Lyman series is formed when the electron returns to the lowest orbit while Balmer series is formed when the electron returns to second. Similarly, Paschen, Breakett and Pfund series are formed when electron returns to the third, fourth and fifth orbits from higher energy orbits respectively (as shown in figure).
Maximum number of different lines produced when electron jump from nth level to ground level is equal to
n(n−1)2.
For example in the case of n=4, number of lines produced is 6.(4→3,4→2,4→1,3→2,3→1,2→1).When an electron returns from n2ton1 state, the number of different
lines in the spectrum will be equal to (n2−n1)(n2−n1+1)2
If the electron comes back from energy level having energy E2 to energy level having energy E1, then the difference may be expressed in terms of energy of photon as:
E2−E1=ΔE,λ=hcΔE,ΔE=hv(v−frequency)
Since h and c are constants ΔE corresponds to definite energy: thus each transition from one energy level to another will produce a light of definite wavelength. This is actually observed as a line in the spectrum of hydrogen atom.
Wave number of line is given by the formula:
¯v=RZ2(1n21−1n22)
where R is a Rydberg constant (R=1.1×107m−1).
(i) First line of a series : It is called line of longest wavelength of line of smallest energy'.
(ii) Series limit or last line of a series : It is the line of shortest wavelength or line of highest energy.
wave number of the first line of Paschen series in Be3+ ion is :
View Solutionthe only electron in the hydrogen atom resides under ordinary conditions in the first orbit. When energy is supplied the electron moves to higher energy orbit depending on the amount of energy absorbed. It emits energy. Lyman series is formed when the electron returns to the lowest orbit while Balmer series is formed when the electron returns to second. Similarly, Paschen, Breakett and Pfund series are formed when electron returns to the third, fourth and fifth orbits from higher energy orbits respectively (as shown in figure).
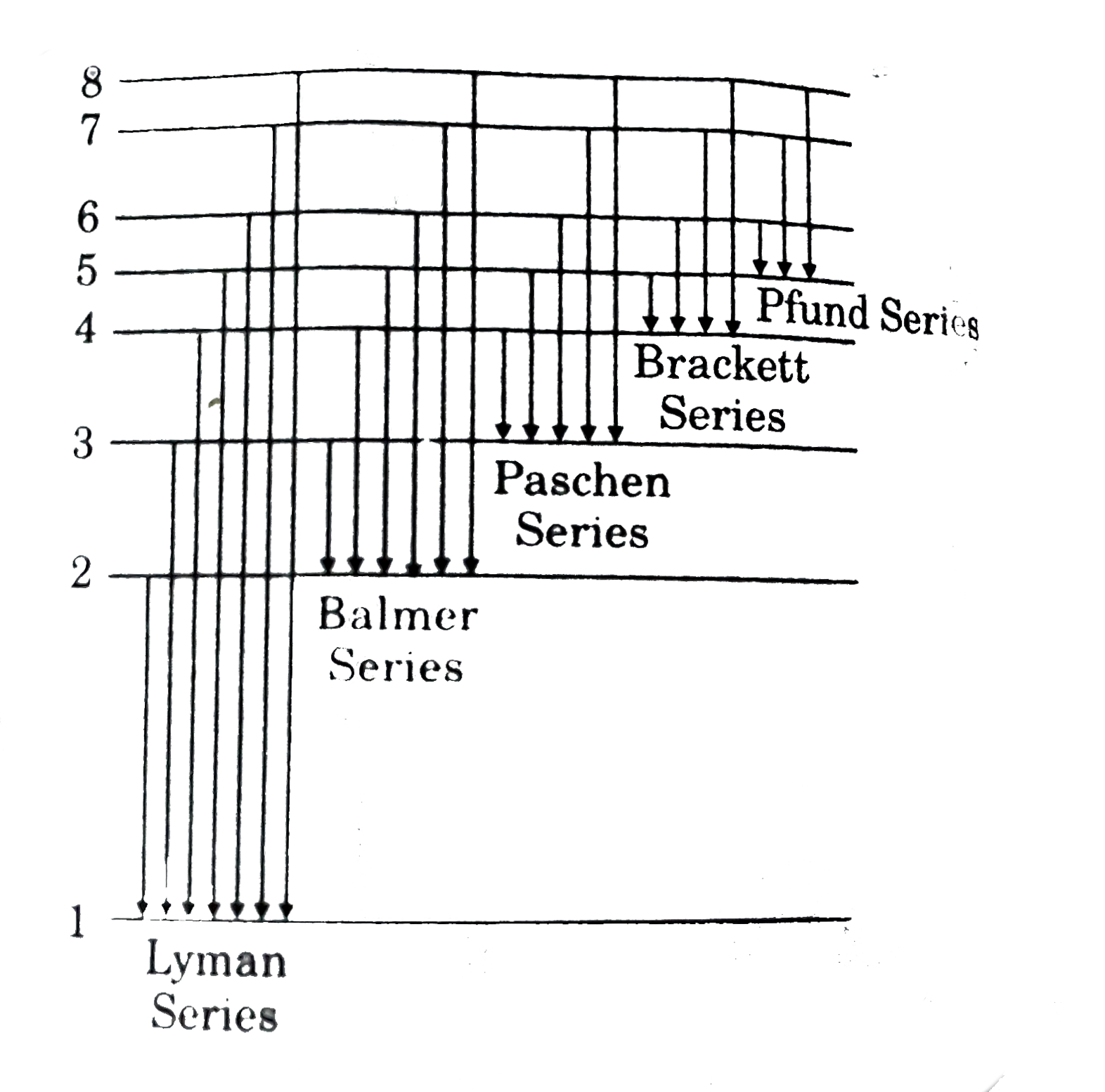
Maximum number of different lines produced when electron jump from nth level to ground level is equal to
n(n−1)2.
For example in the case of n=4, number of lines produced is 6.(4→3,4→2,4→1,3→2,3→1,2→1).When an electron returns from n2ton1 state, the number of different
lines in the spectrum will be equal to (n2−n1)(n2−n1+1)2
If the electron comes back from energy level having energy E2 to energy level having energy E1, then the difference may be expressed in terms of energy of photon as:
E2−E1=ΔE,λ=hcΔE,ΔE=hv(v−frequency)
Since h and c are constants ΔE corresponds to definite energy: thus each transition from one energy level to another will produce a light of definite wavelength. This is actually observed as a line in the spectrum of hydrogen atom.
Wave number of line is given by the formula:
¯v=RZ2(1n21−1n22)
where R is a Rydberg constant (R=1.1×107m−1).
(i) First line of a series : It is called line of longest wavelength of line of smallest energy'.
(ii) Series limit or last line of a series : It is the line of shortest wavelength or line of highest energy.
Consider the following statements
(i) Spectral lines of He+ion belonging to Balmer series are not in visible range.
(ii) In the Balmer series of H-atom maximum lines are in ultraviolet ragion.
(iii) 2nd line of Lyman series of He+ ion has energy 48.35eV
The above statement (i), (ii), (iii) respectively are(T=True,F=False):
View Solution
