The ratios for the energy of the electron in a particular orbit of a single electron species are
[Kinetic : Potential ] and [Total : Kinetic ]
[1:-2] and [-1:1]
[1:2] and [1:1]
[1:1] and [1:2]
[1:2] and [1:2]
The correct Answer is:A
To solve the problem, we need to determine the ratios of kinetic energy to potential energy and total energy to kinetic energy for an electron in a particular orbit according to Bohr's model.
1. Identify the formulas for kinetic and potential energy:
- According to Bohr's model, the kinetic energy (KE) of an electron in orbit is given by:
KE=KZe22R
- The potential energy (PE) of the electron is given by:
PE=−KZe2R
2. Calculate the ratio of kinetic energy to potential energy (KE:PE):
- The ratio can be expressed as:
KEPE=KZe22R−KZe2R
- Simplifying this expression:
KEPE=KZe22R⋅(−RKZe2)=12⋅(−1)=−12
- Therefore, the ratio of kinetic energy to potential energy is:
KE:PE=1:−2
3. Calculate the total energy (TE):
- The total energy (TE) is given by:
TE=KE+PE=KZe22R−KZe2R
- Simplifying this:
TE=KZe22R−2KZe22R=−KZe22R
4. Calculate the ratio of total energy to kinetic energy (TE:KE):
- The ratio can be expressed as:
TEKE=−KZe22RKZe22R
- Simplifying this expression:
TEKE=−1
- Therefore, the ratio of total energy to kinetic energy is:
TE:KE=−1:1
Final Ratios:
- The ratio of kinetic energy to potential energy is 1 : -2.
- The ratio of total energy to kinetic energy is -1 : 1.
- According to Bohr's model, the kinetic energy (KE) of an electron in orbit is given by:
KE=KZe22R
- The potential energy (PE) of the electron is given by:
PE=−KZe2R
- The ratio can be expressed as:
KEPE=KZe22R−KZe2R
- Simplifying this expression:
KEPE=KZe22R⋅(−RKZe2)=12⋅(−1)=−12
- Therefore, the ratio of kinetic energy to potential energy is:
KE:PE=1:−2
- The total energy (TE) is given by:
TE=KE+PE=KZe22R−KZe2R
- Simplifying this:
TE=KZe22R−2KZe22R=−KZe22R
- The ratio can be expressed as:
TEKE=−KZe22RKZe22R
- Simplifying this expression:
TEKE=−1
- Therefore, the ratio of total energy to kinetic energy is:
TE:KE=−1:1
- The ratio of kinetic energy to potential energy is 1 : -2.
- The ratio of total energy to kinetic energy is -1 : 1.
Similar Questions
Kinetic energy of electron in nth orbit in H-atom
View Solutionrn,z= Radius of nth orbit of a single electron species having atomic number 'z'
un,z= Velocity of electron in nth orbit of a single electron specie having atomic number 'z'
En,z= Magnitude of total energy of electron in nth orbit of a single electron species having atomic number 'z'.
Kn,z= Magnitude of kinetic energy of electron in nth orbit of a single electron species having atomic number 'z'
Pn,z= Magnitude of potential energy of electron in nth orbit of a single electron species having atomic number 'z'
fn,z= Frequency of electron in nth orbit of a single electron species having atomic number 'z'.
Tn,z= Time period of electron in nth orbit of a single electron species having atomic number 'z'
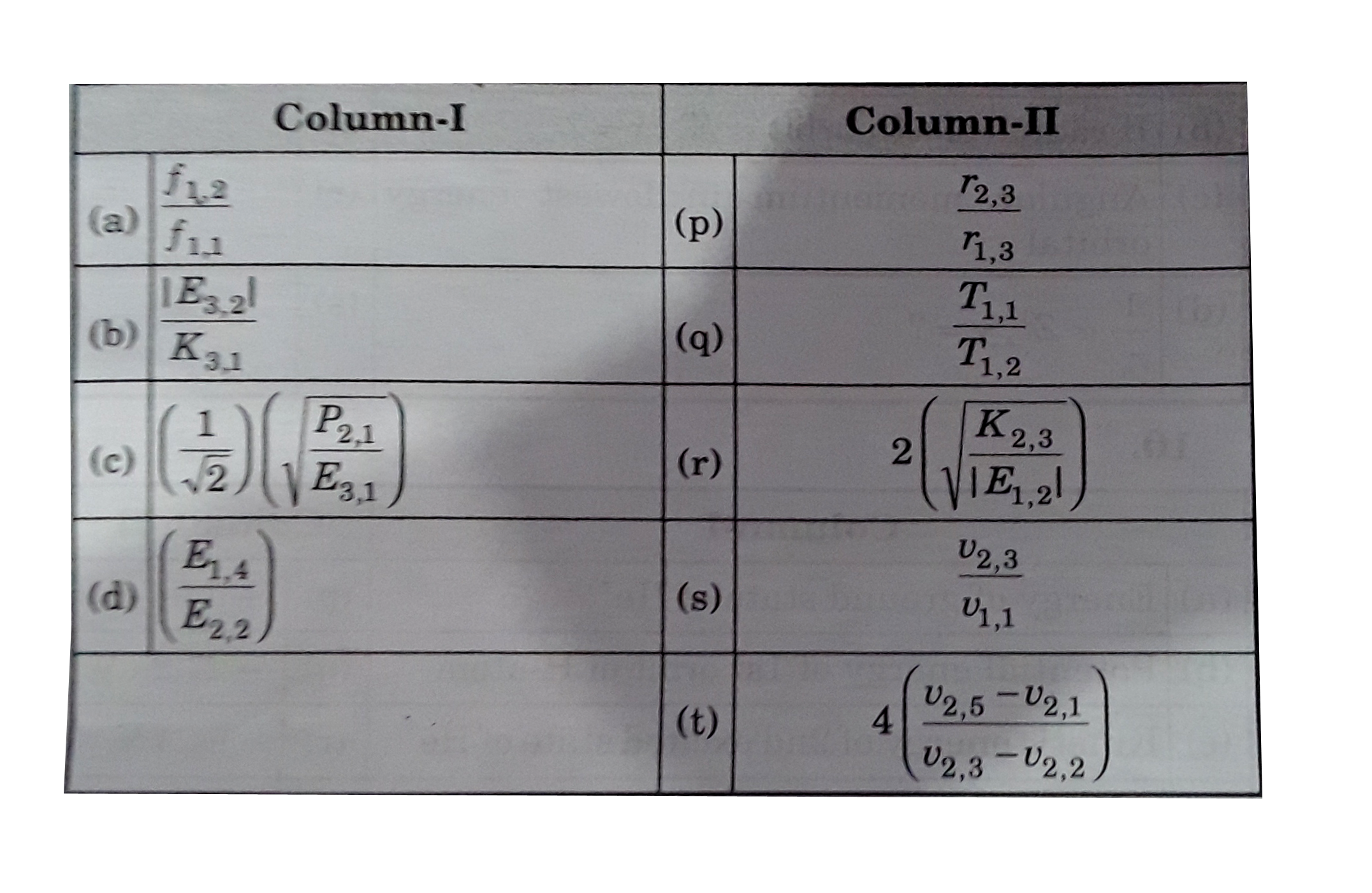
View Solution
Knowledge Check
The kinetic energy of the electron in the nth orbit of an atom is given by the relation
A−4π2me4n2h2B−2π2me4n2h2C−2π2me4n2h2DNone of theseThe total energy of the electron in any orbit of one electron containing species is given by the expression
A−e2/r2B−n2h2/2π2Z2e4mC−2π2mZ2e4/n2h2Dnh/2πThe ratio of potential energy and total energy of an electron in a Bohr orbit of a hydrogen -like species is
A2B-2C1D-1
The ratio of kinetic energy and total energy of an electron in a Bohr of a hydrogen like species is
View SolutionThe ratio of kinetic energy and potential energy of an electron in a Bohr orbit of a hydrogen− like species is :
View SolutionThe ratio of potential energy and total energy of an electron in a Bohr of a hydrogen -like species is
View SolutionKinetic energy of electron in nth orbit is given by
View SolutionThe ratio of kinetic energy and potential energy of an electron in a Bohr of a hydrogen -like species is
View Solution
