Figure explains elevation in boiling point when a non-volatile solute is added to a solvent. Variation of vapour pressure with temperaure and elevation in boiling point is marked.

Elevation in b.p of an aqueous urea solution is 0.52∘(Kb=0.52∘mol−1kg). Hence, mole fraction of urea in this solution is:
0.982
0.0567
0.943
0.018
The correct Answer is:D
Step by step video & text solution for Figure explains elevation in boiling point when a non-volatile solute is added to a solvent. Variation of vapour pressure with temperaure and elevation in boiling point is marked. Elevation in b.p of an aqueous urea solution is 0.52^(@) (K_(b) = 0.52^(@) mol^(-1)kg). Hence, mole fraction of urea in this solution is: by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
Consider following figure and answer the questions at the end of it. Figure explains elevation in boiling point when a non-volatile solute is added to a solvent.
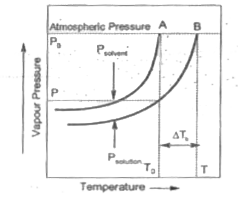
Variation of vapour pressure with temperature and showing elevation in boiling point.
A complex of iron and cyanide ions is 100% ionized at 1m (molal). If elevation in boiling point is 2.08∘(Kb=0.52∘mol−1kg) then the complex is:View SolutionConsider following figure and answer the questions at the end of it.
Figure explains elevation in boiling point when a non-volatile solute is added to a solvent.
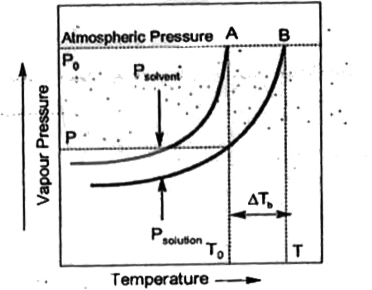
Variation of vapour pressure with temperature and showing elevation in boiling point.
A complex of iron and cyanide ions is 100% ionized at 1m (molal). If its elevation in boiling point is 2.08∘(Kb=0.52∘mol−1kg) then the complex isView Solution
Knowledge Check
- Question 1 - Select One
Elevation in b.p. of an aqueous urea solution is 0.52∘,(Kb=0.622∘mol−1kg) Hence, mole-fraction of urea in this solution is :
A0.982B0.567C0.943D0.018 - Question 2 - Select One
Consider following figure and answer the questions at the end of it. Figure explains elevation in boiling point when a non-volatile solute is added to a solvent.
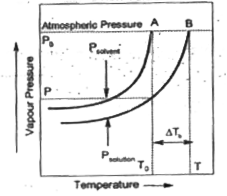
Variation of vapour pressure with temperature and showing elevation in boiling point.
Elevation in boiling point of an aqueous urea solution is 0.52∘.(Kb=0.52∘mol−1kg). Hence, mole fraction of urea in this solution is:A0.982B0.0567C0.943D0.018 - Question 3 - Select One
Consider following figure and answer the questions at the end of it.
Figure explains elevation in boiling point when a non-volatile solute is added to a solvent.
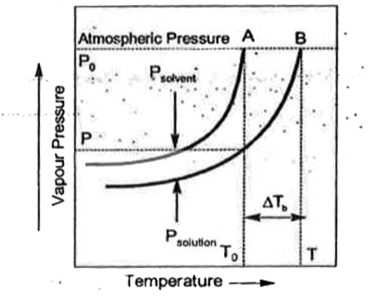
Variation of vapour pressure with temperature and showing elevation in boiling point.
Elevation in boiling point of an aqueous urea solution is 0.52∘. (Kb=0.52∘mol−1kg). Hence, mole fraction of urea in this solution isA0.982B0.0567C0.943D0.018
Figure explains elevation in boiling point when a non-volatile solute is added to a solvent. Variation of vapour pressure with temperaure and elevation in boiling point is marked.

Given that ΔTb is the elevation in boiling point of the solvent in a solution of molarity m then limm→0(ΔTbm) is equal to:View SolutionFigure explains elevation in boiling point when a non-volatile solute is added to a solvent. Variation of vapour pressure with temperaure and elevation in boiling point is marked.

Ratio of ΔTb/Kb of 6%AB2 and 9%A2B(AB2 and A2B both are non-electrolytes) is 1 mol/kg in both cases. Hence, atomic masses of A and B are respectively.View SolutionElevation in boiling point of an aqueous solution of urea is 0.52(kbfor water=0.52Kmolality−1). The mole fraction is urea in this solution is :
View SolutionConsider following figure and answer the questions at the end of it. Figure explains elevation in boiling point when a non-volatile solute is added to a solvent.
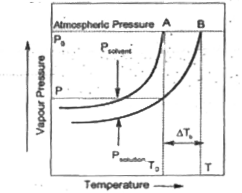
Variation of vapour pressure with temperature and showing elevation in boiling point.
Given that ΔTb is the elevation in boiling point of the solvent in a solution of molality m then Ltm→0(ΔTbm) is equal toView SolutionConsider following figure and answer the questions at the end of it.
Figure explains elevation in boiling point when a non-volatile solute is added to a solvent.
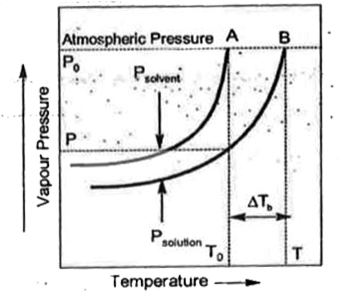
Variation of vapour pressure with temperature and showing elevation in boiling point.
Given that ΔTb is the elevation in boiling point of the solvent in a solution of molality 'm' then Ltm→0(DηlTbm) is equal toView Solution
