Two identical gases whose adiabatic exponent is are filled in two identical containers at equal pressures. In both the containers the volume of gas is doubled. In first container it is done by an isothermal process and in second container it is done by adiabatic process. Find the condition for which the work done by the gas in the two expansion process is same.
The correct Answer is:
To solve the problem, we need to find the condition under which the work done by the gas in an isothermal expansion is equal to the work done in an adiabatic expansion. Let's break it down step by step.
Step 1: Define the Initial Conditions
Let the initial pressure and volume of both gases be:
- Initial pressure, P0
- Initial volume, V0
Step 2: Work Done in Isothermal Expansion
For the isothermal process, the work done W1 when the volume is doubled (final volume Vf=2V0) is given by:
W1=nRTln(VfVi)
Since P0V0=nRT, we can substitute nRT with P0V0:
W1=P0V0ln(2V0V0)=P0V0ln(2)
Step 3: Work Done in Adiabatic Expansion
For the adiabatic process, we use the relation PVγ=constant. The final pressure Pf can be expressed as:
PfVγf=P0Vγ0
Substituting Vf=2V0:
Pf(2V0)γ=P0Vγ0
This simplifies to:
Pf=P0⋅2−γ+1
The work done W2 in the adiabatic process is given by:
W2=PfVf−P0V0γ−1
Substituting Pf and Vf:
W2=P0⋅2−γ+1⋅2V0−P0V0γ−1
This simplifies to:
W2=P0V0(2⋅2−γ+1−1)γ−1
W2=P0V0(22−γ−1)γ−1
Step 4: Equate the Work Done
To find the condition for which the work done in both processes is the same:
W1=W2
Substituting the expressions we derived:
P0V0ln(2)=P0V0(22−γ−1)γ−1
Dividing both sides by P0V0 (assuming P0V0≠0):
ln(2)=22−γ−1γ−1
Final Condition
Thus, the condition for which the work done by the gas in both expansion processes is the same is:
ln(2)=22−γ−1γ−1
Let the initial pressure and volume of both gases be:
- Initial pressure, P0
- Initial volume, V0
For the isothermal process, the work done W1 when the volume is doubled (final volume Vf=2V0) is given by:
W1=nRTln(VfVi)
Since P0V0=nRT, we can substitute nRT with P0V0:
W1=P0V0ln(2V0V0)=P0V0ln(2)
For the adiabatic process, we use the relation PVγ=constant. The final pressure Pf can be expressed as:
PfVγf=P0Vγ0
Substituting Vf=2V0:
Pf(2V0)γ=P0Vγ0
This simplifies to:
Pf=P0⋅2−γ+1
W2=PfVf−P0V0γ−1
Substituting Pf and Vf:
W2=P0⋅2−γ+1⋅2V0−P0V0γ−1
This simplifies to:
W2=P0V0(2⋅2−γ+1−1)γ−1
W2=P0V0(22−γ−1)γ−1
To find the condition for which the work done in both processes is the same:
W1=W2
Substituting the expressions we derived:
P0V0ln(2)=P0V0(22−γ−1)γ−1
Dividing both sides by P0V0 (assuming P0V0≠0):
ln(2)=22−γ−1γ−1
Thus, the condition for which the work done by the gas in both expansion processes is the same is:
ln(2)=22−γ−1γ−1
Topper's Solved these Questions
- THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES Book:PHYSICS GALAXY - ASHISH ARORAChapter:THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES Exercise:Practice Exercise 3.4
Explore 11 Videos
- THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES Book:PHYSICS GALAXY - ASHISH ARORAChapter:THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES Exercise:Practice Exercise 3.1
Explore 6 Videos
- PHOTOELECTRIC EFFECT AND MATTER WAVESBook:PHYSICS GALAXY - ASHISH ARORAChapter:PHOTOELECTRIC EFFECT AND MATTER WAVESExercise:Unsolved numerical problems
Explore 42 Videos
- WAVE OPTICSBook:PHYSICS GALAXY - ASHISH ARORAChapter:WAVE OPTICSExercise:Unsolved Numerical Problems
Explore 28 Videos
Similar Questions
Knowledge Check
Initial pressure and volume of a gas are P and V respectively. First its volume is expanded to 4V by isothermal process and then again its volume makes to be V by adiabatic process then its final pressure is (γ=1.5) -
A8PB4PCPD2PIn an adiabatic process 90 J of work is done on the gas. The change in internal energy of the gas is
A−90jB+90jC0 jDDepends on initial temperatureAssertion: In a thermodynamic process, initial volume of gas is equal to final volume of gas. Work done by gas in this process should be zero
Reason: Work done by gas in isochoric process is zero.A(a) If both Assertion and Reason are true and the Reason is correct explanation of the Assertion.B(b) If both Assertion and Reason are true but Reason is not the correct explanation of Assertion.C(c) If Assertion is true, but the Reason is false.D(d) If Assertion is false but the Reason is true.
Three identical diatomic gases (γ=1.5) are enclosed in three identical containers but at different pressures and same temperatures. These gases are expanded to double their volumes in first container the process is isothermal, in second container the process is adiabatic and in third container process is isobaric. Of The final pressures are equal in the three containers, find the ratio of the initial pressures in the three containers.
View SolutionLet QandW denote the amount of heat given to an ideal gas the work done by it in an adiabatic process.
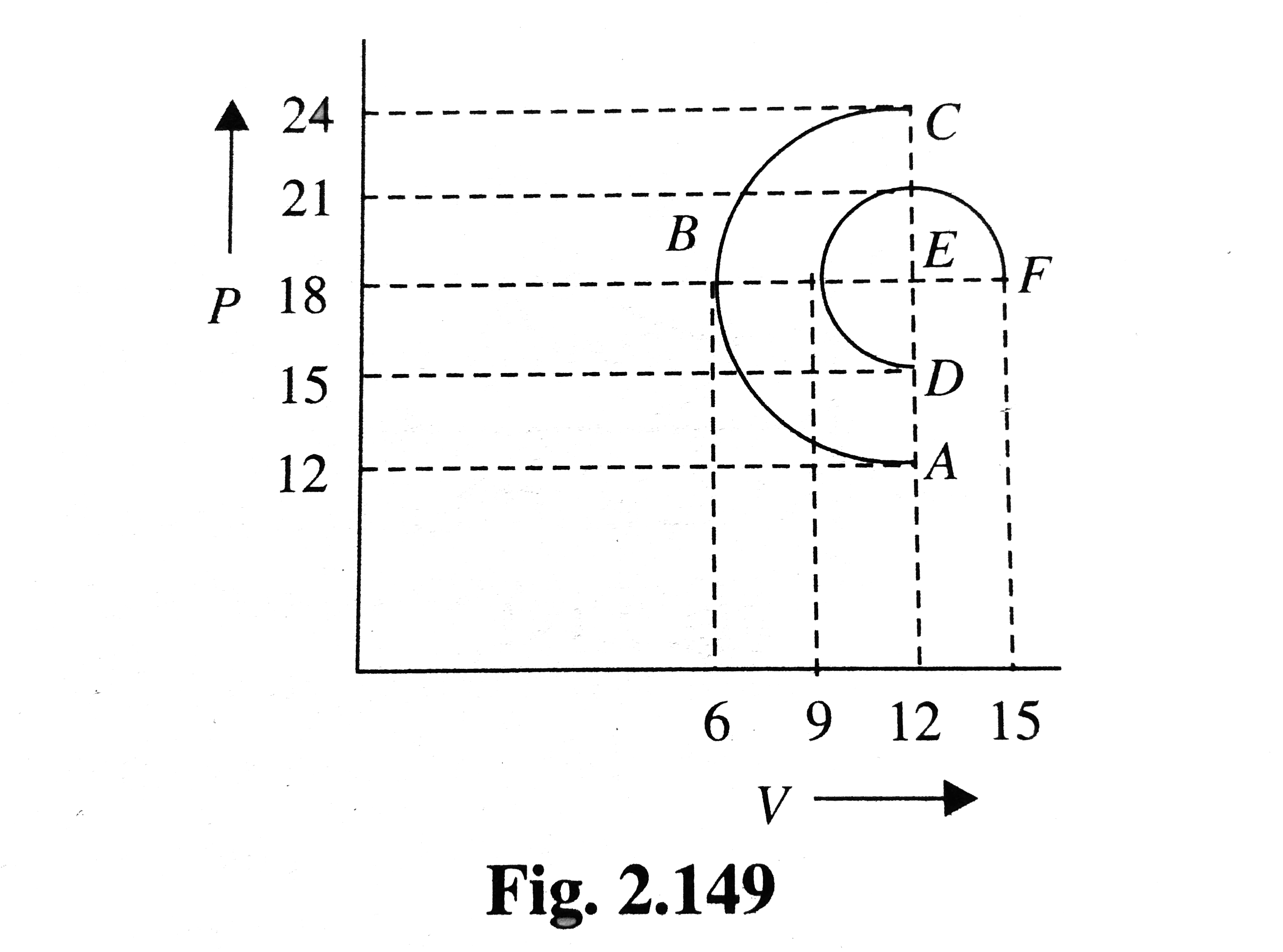
View SolutionThere are two process ABC and DEF. In which of the process is the amount of work done by the gas is greater ?
View SolutionThe internal energy of a system remains constant when it undergoes
(i) a cyclic process
(ii) an isothermal process
(iii) an adiabatic process
(iv) any process in which the heat given out by the system equal to the work done on the system
View SolutionAn ideal gas with adiabatic exponent (γ=1.5) undergoes a process in which work done by the gas is same as increase in internal energy of the gas. Here R is gas constant. The molar heat capacity C of gas for the process is:
View Solution