The equation of state for n moles of an ideal gas is PV=nRT, where R is a constant. The SI unit for R is:
JK−1 per molecule
Jkg−1K−1
JK−1mol−1
JK−1g−1
To find the SI unit of the constant R in the ideal gas equation PV=nRT, we can follow these steps:
1. Understand the Ideal Gas Law: The equation PV=nRT relates pressure (P), volume (V), number of moles (n), the gas constant (R), and temperature (T).
2. Identify the Units:
- Pressure (P) is measured in pascals (Pa), which is equivalent to N/m2 or kg/(m⋅s2).
- Volume (V) is measured in cubic meters (m³).
- The number of moles (n) is measured in moles (mol).
- Temperature (T) is measured in kelvins (K).
3. Rearrange the Ideal Gas Law: To find the unit of R, we can rearrange the equation:
R=PVnT
4. Substitute the Units:
- Substitute the units into the equation:
R=(Pa)(m3)mol⋅K
- Since Pa=N/m2=kg/(m⋅s2), we can rewrite it as:
R = \frac{(\text{kg/(m·s}^2)}(\text{m}^3)}{\text{mol} \cdot \text{K}} = \frac{\text{kg} \cdot \text{m}^2}{\text{s}^2 \cdot \text{mol} \cdot \text{K}}
5. Final Unit of R: Therefore, the SI unit of R is:
J/(mol⋅K)
where J (joule) is the unit of energy, and it can be expressed as kg⋅m2/s2.
Conclusion:
The SI unit for the gas constant R is J/(mol⋅K).
---
- Pressure (P) is measured in pascals (Pa), which is equivalent to N/m2 or kg/(m⋅s2).
- Volume (V) is measured in cubic meters (m³).
- The number of moles (n) is measured in moles (mol).
- Temperature (T) is measured in kelvins (K).
R=PVnT
- Substitute the units into the equation:
R=(Pa)(m3)mol⋅K
- Since Pa=N/m2=kg/(m⋅s2), we can rewrite it as:
R = \frac{(\text{kg/(m·s}^2)}(\text{m}^3)}{\text{mol} \cdot \text{K}} = \frac{\text{kg} \cdot \text{m}^2}{\text{s}^2 \cdot \text{mol} \cdot \text{K}}
J/(mol⋅K)
where J (joule) is the unit of energy, and it can be expressed as kg⋅m2/s2.
The SI unit for the gas constant R is J/(mol⋅K).
Topper's Solved these Questions
- THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES Book:PHYSICS GALAXY - ASHISH ARORAChapter:THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES Exercise:Advance MCQs with One or More Options Correct
Explore 10 Videos
- THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES Book:PHYSICS GALAXY - ASHISH ARORAChapter:THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES Exercise:Unsolved Numerical Problems
Explore 100 Videos
- THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES Book:PHYSICS GALAXY - ASHISH ARORAChapter:THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES Exercise:Conceptual MCQs Single Option Correct
Explore 21 Videos
- PHOTOELECTRIC EFFECT AND MATTER WAVESBook:PHYSICS GALAXY - ASHISH ARORAChapter:PHOTOELECTRIC EFFECT AND MATTER WAVESExercise:Unsolved numerical problems
Explore 42 Videos
- WAVE OPTICSBook:PHYSICS GALAXY - ASHISH ARORAChapter:WAVE OPTICSExercise:Unsolved Numerical Problems
Explore 28 Videos
Similar Questions
Knowledge Check
In the equation of state of an ideal gas PV =nRT , the value of the universal gas constant is not correct :
A8.314 JK−1mol−1B0.0821 atm L mol−1K−1C0.8314 bar L mol−1K−1D2 cal mol−1K−1In the equation of state of an ideal gas PV = nRT, the value of universal gas constant would depend only on :
Athe nature of the gasBthe units of measurementCthe pressure of the gasDthe pressure of the gasValue of gas constant 'R' for one mole of an ideal gas is,-
A8.314cal K−1 mol−1B8.314JK−1mol−1C8.314KJK−1mol−1DNone of these
35.The equation of state of a gas is a P(V-nb)= nRT.Where b and R are constant.If the Pressure and Temperature are such that molar volume Vm=10b and compressibility factor of the gas is 10x find the value of x?
View SolutionIn the equation of state of an ideal gas PV = nRT, the value of universal gas constant would depend only on :
View SolutionIn the equation of state of an ideal gas PV = nRT, the value of universal gas constant would depend only on :
View SolutionThe gas equation for n moles of a real gas is (P+aV2)(V−b)=nRT where P is the pressure, V is the volume, T is the absolute temperature, R is the molar gas constant and a, b are arbitrary constants. Which of the following have the same dimensions as those of PV ?
View SolutionThe ideal gas equation for 1 mol of ideal gas is PV = nRT
graph between P and T at constant volume, i.e. isochores are plotted as under
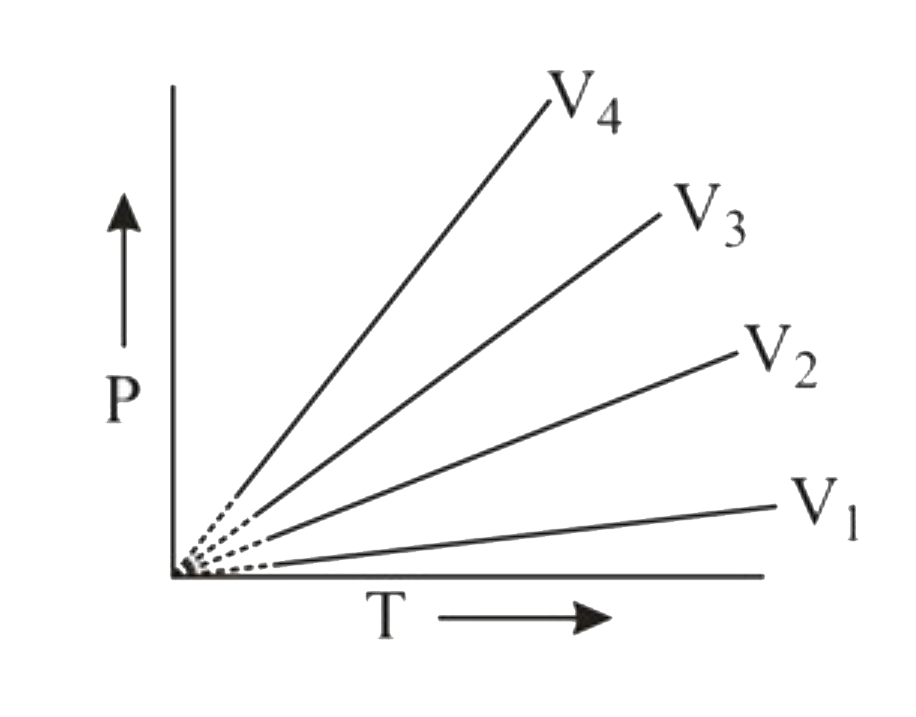
Which of the following order of volume is correct ?
View Solution

