Cubic close packing arrangement is also referred to as:
Hexagonal close packing
Face centred cubic
Body centred cubic
None of these
The correct Answer is:B
To solve the question regarding what the cubic close packing arrangement is also referred to as, we can follow these steps:
1. Understanding Cubic Close Packing (CCP):
- Cubic close packing is a way of arranging spheres (or atoms) in three-dimensional space to maximize the density of the arrangement.
2. Identifying the Acronym:
- The acronym for cubic close packing is CCP. This arrangement is also known as face-centered cubic (FCC).
3. Defining Face-Centered Cubic (FCC):
- In FCC, atoms are located at each corner of the cube and at the centers of all the faces of the cube. This arrangement allows for a high packing efficiency.
4. Recognizing the Pattern:
- The arrangement of atoms in cubic close packing follows an ABC stacking sequence. This means that the layers are stacked in a specific order to maintain the close packing.
5. Conclusion:
- Therefore, the cubic close packing arrangement is also referred to as face-centered cubic (FCC).
Final Answer:
Cubic close packing arrangement is also referred to as Face-Centered Cubic (FCC).
---
- Cubic close packing is a way of arranging spheres (or atoms) in three-dimensional space to maximize the density of the arrangement.
- The acronym for cubic close packing is CCP. This arrangement is also known as face-centered cubic (FCC).
- In FCC, atoms are located at each corner of the cube and at the centers of all the faces of the cube. This arrangement allows for a high packing efficiency.
- The arrangement of atoms in cubic close packing follows an ABC stacking sequence. This means that the layers are stacked in a specific order to maintain the close packing.
- Therefore, the cubic close packing arrangement is also referred to as face-centered cubic (FCC).
Cubic close packing arrangement is also referred to as Face-Centered Cubic (FCC).
Similar Questions
The empirical formula for a compound with a cubic close packed arrangement of anions and with cations occupying all the octahedral sites in AxB. The value of x is _________.
View SolutionSilver metal crystallises in a cubic closed- packed arrangement with the edge of the unit cell having a length, a = 407 pm. What is the radius of silver atom?
View Solution
Knowledge Check
The total number of identical spheres required in cubic close packing arrangement of a unit cell is
A6B8C12D14In a compound,oxide ions are arranged in cubic close packing arrangement. Cations A occupy one-sixth of the tetrahdral voids and cations B occupy one-third of the octahedral voids. The formula of the compound is
AA2BO3BAB2O3CA2B2O2DABO3A compound MpXq has cubic close packing (p) arrangement of X. Its unit cell structure is shown below. The empirical formula of the compound is
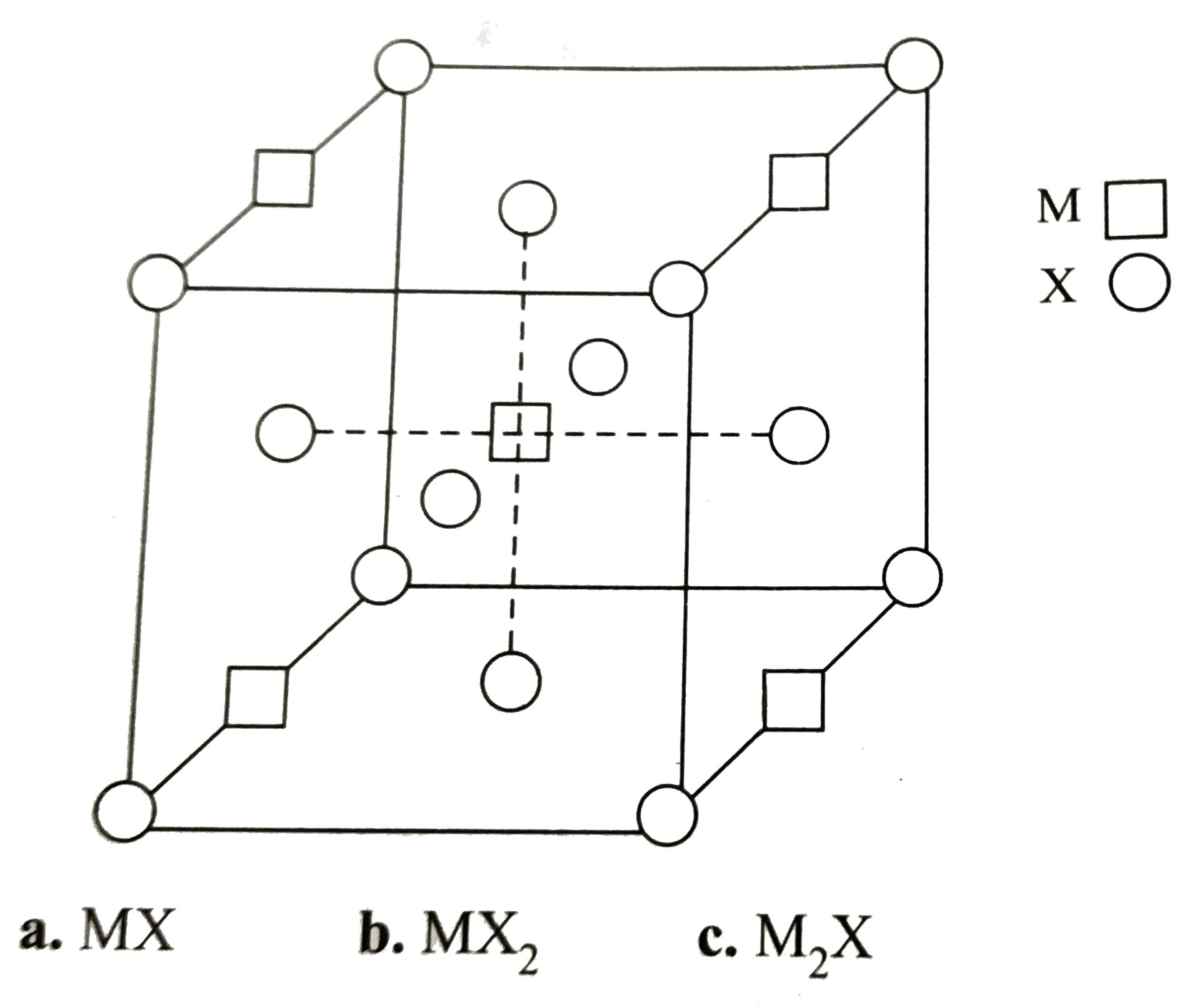 AMXBMX2CM2XDM5X14
AMXBMX2CM2XDM5X14
Silver metal crystallises in a cubic closed packed arrangement with edge length 404 pm .Thus radius of the silver atom is
View SolutionThree-dimensional close packing in solids is referred to as stacking the second square closed packing exactly above the first. In this tight packing, the spheres are horizontally and vertically correctly balanced. Similarly, we can obtain a simple cubic lattice by adding more layers, one above the other. This can be done in two ways. Three-dimensional close packing from two-dimensional square close-packed layers: By putting the second square closed packing exactly above the first, it is possible to form three-dimensional close packing. In this tight packing, the spheres are horizontally and vertically correctly balanced. Similarly, we can obtain a simple cubic lattice by adding more layers, one above the other.Three-dimensional close packing from two-dimensional hexagonal close-packed layers: With the assistance, of two-dimensional hexagonal packed layers, three-dimensional close packing can be obtained.
The coordination number of cubic closed packing is:
View SolutionThree-dimensional close packing in solids is referred to as stacking the second square closed packing exactly above the first. In this tight packing, the spheres are horizontally and vertically correctly balanced. Similarly, we can obtain a simple cubic lattice by adding more layers, one above the other. This can be done in two ways. Three-dimensional close packing from two-dimensional square close-packed layers: By putting the second square closed packing exactly above the first, it is possible to form three-dimensional close packing. In this tight packing, the spheres are horizontally and vertically correctly balanced. Similarly, we can obtain a simple cubic lattice by adding more layers, one above the other.Three-dimensional close packing from two-dimensional hexagonal close-packed layers: With the assistance, of two-dimensional hexagonal packed layers, three-dimensional close packing can be obtained.
The correct statement about zns crystal is:
View SolutionThree-dimensional close packing in solids is referred to as stacking the second square closed packing exactly above the first. In this tight packing, the spheres are horizontally and vertically correctly balanced. Similarly, we can obtain a simple cubic lattice by adding more layers, one above the other. This can be done in two ways. Three-dimensional close packing from two-dimensional square close-packed layers: By putting the second square closed packing exactly above the first, it is possible to form three-dimensional close packing. In this tight packing, the spheres are horizontally and vertically correctly balanced. Similarly, we can obtain a simple cubic lattice by adding more layers, one above the other.Three-dimensional close packing from two-dimensional hexagonal close-packed layers: With the assistance, of two-dimensional hexagonal packed layers, three-dimensional close packing can be obtained.
What will be the ratio of radii of the spheres in cubic systems simple cubic, body centred cubic and face centred cubic systems. if 'a' stands for the edge length.
View SolutionPacking refers to the arrangement of constituent units in such a way that the forces of attraction among the constituent particles is the maximum and the contituents occupy the maximum available space. In two dimensions, there are hexagonal close packing and cubic close packing. In three dimentions, there are hexagonal, cubic as well as body centred close packings.
A certain oxide of a metal M crystallises in such a way that O2− ions occupy hcp arrangement following ABAB... pattern. The metal ions however occupy 2/3 rd of the octahedral voids. The formula of the compound is :
View Solution
