Between two coherent waves phase is:
f(x) = constant
(t) = constant
f(d) = f(t) = constant
f(x) = f(t)
The correct Answer is:A
To solve the question regarding the phase between two coherent waves, we can follow these steps:
1. Understanding Coherent Waves:
- Coherent waves are waves that maintain a constant phase relationship. This means that the phase difference between the two waves does not change over time.
2. Definition of Phase:
- The phase of a wave can be defined as the position of a point in time on a waveform cycle. It is usually measured in radians or degrees.
3. Constant Phase Difference:
- For two coherent sources, if the phase difference is initially set at a certain value (for example, π/4 or π/6), this phase difference will remain constant over time.
4. Conclusion:
- Therefore, the phase between two coherent waves is constant. This means that if the initial phase difference is π/4, it will always be π/4, regardless of the time or position.
5. Final Answer:
- The phase between two coherent waves is constant.
- Coherent waves are waves that maintain a constant phase relationship. This means that the phase difference between the two waves does not change over time.
- The phase of a wave can be defined as the position of a point in time on a waveform cycle. It is usually measured in radians or degrees.
- For two coherent sources, if the phase difference is initially set at a certain value (for example, π/4 or π/6), this phase difference will remain constant over time.
- Therefore, the phase between two coherent waves is constant. This means that if the initial phase difference is π/4, it will always be π/4, regardless of the time or position.
- The phase between two coherent waves is constant.
Similar Questions
Knowledge Check
The amplitudes of two coherent waves are vector quanti- ties. In the given table, Column I shows the phase differ ence between two coherent waves, Column II shows the path difference between them and Column III shows their resultant amplitudes.
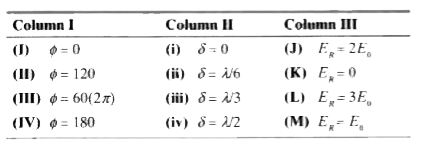
When is ER maximum?A(I) (ii) (M)B(III) (ii) (J)C(II) (ii) (K)D(II) (iv) (M)The amplitudes of two coherent waves are vector quanti- ties. In the given table, Column I shows the phase differ ence between two coherent waves, Column II shows the path difference between them and Column III shows their resultant amplitudes.

When is the phasor diagram at primary maxima?A(I) (iii) (M)B(III) (ii) (K)C(I) (i) (L)D(I) (iii) (J)The amplitudes of two coherent waves are vector quanti- ties. In the given table, Column I shows the phase differ ence between two coherent waves, Column II shows the path difference between them and Column III shows their resultant amplitudes.
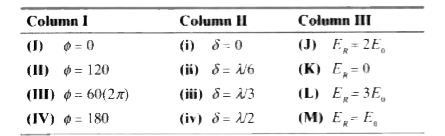
When is the phasor diagram at secondary maxima?A(III) (i) (L)B(IV) (i) (J)C(III) (iv) (J)D(IV) (iv) (M)
The relationship between phase difference Δϕ and the path difference Δr between two interfering waves is given by: (λ = wavelength)
View SolutionThe phase between the two successive M phase is called as
View SolutionIf two coherent light waves produce minima of fifth order, the path difference between the waves is-
View SolutionFor constructive interference, the phase difference between the two interfering waves is
View SolutionAssertion: Three waves of equal amplitudes interfere at a point. Phase difference between two successive waves is π2. Then, resultant intensity is same as the intensity due to individual wave.
Reason: Two different light sources are never coherent.
View Solution
