Force per unit length acting at one end of each of the two long parallel wires, carrying current I each, kept distance r apart is
μ04πi2r
μ04π2i2r
μ04π(2i)2r
μ04πi24r
The correct Answer is:B
To find the force per unit length acting at one end of two long parallel wires carrying current I each and separated by a distance r, we can follow these steps:
Step 1: Understand the Concept
When two parallel wires carry current, they exert a force on each other. The direction of this force depends on the direction of the currents. If the currents are in the same direction, the force is attractive; if they are in opposite directions, the force is repulsive.
Step 2: Use the Formula for Force per Unit Length
The formula for the force per unit length FL between two parallel wires carrying currents I1 and I2 separated by a distance r is given by:
FL=μ02π⋅I1I2r
Where:
- μ0 is the permeability of free space (4π×10−7T m/A).
- I1 and I2 are the currents in the wires.
- r is the distance between the wires.
Step 3: Substitute the Values
Since both wires carry the same current I, we can set I1=I2=I. Thus, the formula simplifies to:
FL=μ02π⋅I2r
Step 4: Final Expression
Now we can express the force per unit length acting on each wire:
FL=μ0I22πr
Step 5: Simplify the Expression
To match the format often used in physics problems, we can multiply and divide by 2:
FL=μ04π⋅2I2r
Conclusion
Thus, the final expression for the force per unit length acting on one end of each of the two long parallel wires is:
FL=μ04π⋅2I2r
When two parallel wires carry current, they exert a force on each other. The direction of this force depends on the direction of the currents. If the currents are in the same direction, the force is attractive; if they are in opposite directions, the force is repulsive.
The formula for the force per unit length FL between two parallel wires carrying currents I1 and I2 separated by a distance r is given by:
- μ0 is the permeability of free space (4π×10−7T m/A).
- I1 and I2 are the currents in the wires.
- r is the distance between the wires.
Since both wires carry the same current I, we can set I1=I2=I. Thus, the formula simplifies to:
Now we can express the force per unit length acting on each wire:
To match the format often used in physics problems, we can multiply and divide by 2:
Thus, the final expression for the force per unit length acting on one end of each of the two long parallel wires is:
Similar Questions
Calculate the force per unit length on a long straight wire carrying current 4A due to parallel wire carrying current 6A current. Distance between the wires =3cm.
View SolutionCalculate the force per unit length on a long straight wire carrying current of 4 A due to a parallel wire carrying 6 A current . Distance between the wires is 3 cm.
View Solution
Knowledge Check
The force acting per unit length on one conductor due to the other for two long parallel current - carrying wires is
Aμ04πI1I2rBμ04πI1I2rCμ04π2I1I2rDμ04πI1I24rThe graph of force per unit legth between two long parallel current carrying conductors and the reciprocal of the distance between them is
Aa parabolaBa circleCa reactangular hyperbolaDa straight lineThe graph of force per unit legth between two long parallel current carrying conductors and the reciprocal of the distance between them is
AStraight lineBParabolaCEllipseDRectangular hyperbola
Calculate the self inductance per unit length of a current loop formed by joining the ends of two long parallel wires of radius r separated by a distance d between their axes, neglecting the end effects and magnetic flux within the wires.
View SolutionTwo linear parallel conductors carrying currents in the same direction attract each other and two linear parallel conductors carrying currents in opposite direction repel each other. The force acting per unit length due to currents I1 and I2 in two linear parallel conductors held distance r apart in vacuum in SI unit is F=μ04π2I1I2r
Read the above passage and answer the following questions:
(i) What is the basic reason for the force between two linear parallel conductors carrying currents?
(ii) Two straight wires A and B of lengths 2cm and 20cm, carrying currents 2⋅0A and 5⋅0A respectively in opposite directions are lying parallel to each other 4⋅0cm apart. The wire A is held near the middle of wire B. What is the force on 20cm long wire B?
(iii) What does this study imply in day to day life?
View Solution(a) Derive the expression for the force acting per unit length between two long straight parallel current carrying conductors. Hence, define one ampere.
(b) Two long parallel straight conductors are placed 12 cm apart in air. They carry equal currents of 3 A each. Find the magnitude and direction of the magnetic field at a point midway between them (drawing a figure) when the currents in them flow in opposite directions.
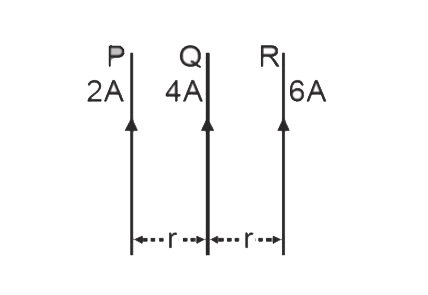
View SolutionP, Q and R long parallel straight wires in air, carrying currents as shown. The direction of resultant force on R is :-
View SolutionThe force per unit length between two parallel long current carrying conductor is F. If the current in each conductor is tripled, what would be the value of the force per unit length between them?
View Solution

