A gymnast does many acrobats in air before descending on the floor. The quantity conserved, consequent to motion, is:
angular velocity
M.I.
linear momentum
angular momentum
The correct Answer is:D
To solve the question regarding the gymnast performing acrobatics in the air and identifying the conserved quantity, we can follow these steps:
1. Understanding the Motion:
The gymnast performs acrobatic movements in the air, which involves rotation and changes in body position.
2. Identifying Relevant Physics Concepts:
In rotational motion, one key principle is the conservation of angular momentum. Angular momentum (L) is given by the product of the moment of inertia (I) and angular velocity (ω):
L=I⋅ω
3. Moment of Inertia and Angular Velocity:
As the gymnast changes position (for example, by folding their arms), the moment of inertia changes. When the arms are extended, the moment of inertia is larger. When the gymnast folds their arms, the moment of inertia decreases.
4. Applying Conservation of Angular Momentum:
According to the conservation of angular momentum:
I1⋅ω1=I2⋅ω2
where I1 and I2 are the moments of inertia before and after the gymnast folds their arms, and ω1 and ω2 are the corresponding angular velocities.
5. Conclusion:
When the gymnast folds their arms, the moment of inertia decreases, which causes the angular velocity to increase in order to conserve angular momentum. Thus, the quantity that is conserved during the gymnast's motion is angular momentum.
Final Answer:
The quantity conserved, consequent to the gymnast's motion, is angular momentum.
---
The gymnast performs acrobatic movements in the air, which involves rotation and changes in body position.
In rotational motion, one key principle is the conservation of angular momentum. Angular momentum (L) is given by the product of the moment of inertia (I) and angular velocity (ω):
L=I⋅ω
As the gymnast changes position (for example, by folding their arms), the moment of inertia changes. When the arms are extended, the moment of inertia is larger. When the gymnast folds their arms, the moment of inertia decreases.
According to the conservation of angular momentum:
I1⋅ω1=I2⋅ω2
where I1 and I2 are the moments of inertia before and after the gymnast folds their arms, and ω1 and ω2 are the corresponding angular velocities.
When the gymnast folds their arms, the moment of inertia decreases, which causes the angular velocity to increase in order to conserve angular momentum. Thus, the quantity that is conserved during the gymnast's motion is angular momentum.
The quantity conserved, consequent to the gymnast's motion, is angular momentum.
Similar Questions
A body explodeds in mid - air. Does its momentum remain conserved ?
View SolutionIn the system shown in figure the masses of the bodies are known to be m1 and m2, the coefficient of friction between the body m1 and the horizontal plane is equal to k, and a pulley of mass m is assumed to be a uniform disc. The thread does not slip over the pulley. At the moment t=0 the body m2 starts descending. Assuming the mass of the thread and the friction in the axle of the pulley to be negligible, find the work performed by the friction forces acting on the body m1 over the first t seconds after the beginning of motion.

View Solution
Knowledge Check
In the motion of a rocket, the quantity which is conserved is
AFroceBmassCLinear momentumDKinetic energyFor uniform circular motion, the quantity that does remain constant is
Acentripetal accelerationBkinetic energyCangular momentumDangular velocityA golfer imparts a speed of 30.3 m/s to a ball, and it travels the maximum possible distance before landing on the green. The tee and the green are at the same elevation. How much time does the ball spend in the air?
A4.37 sB2.68 sC3.51 sD1.84 s
In the Suniti building in Mumbai there are 12 floors plus the ground floor. 9 people get into the lift of the building on the ground floor. The lift does not stop on the first floor. If 2, 3 and 4 people alight from the lift on its upward journey, then in how many ways can they do so? (Assume they alight on different floors.)
View SolutionThe graph as shown in. below descrines the motion of a ball rebounding from a horizontal surface being released from a point above the surface. Assume that the ball colledes each time with the floor inelastically. The quantity represented on the y-axis in the is the balls (take upward direction as positive)
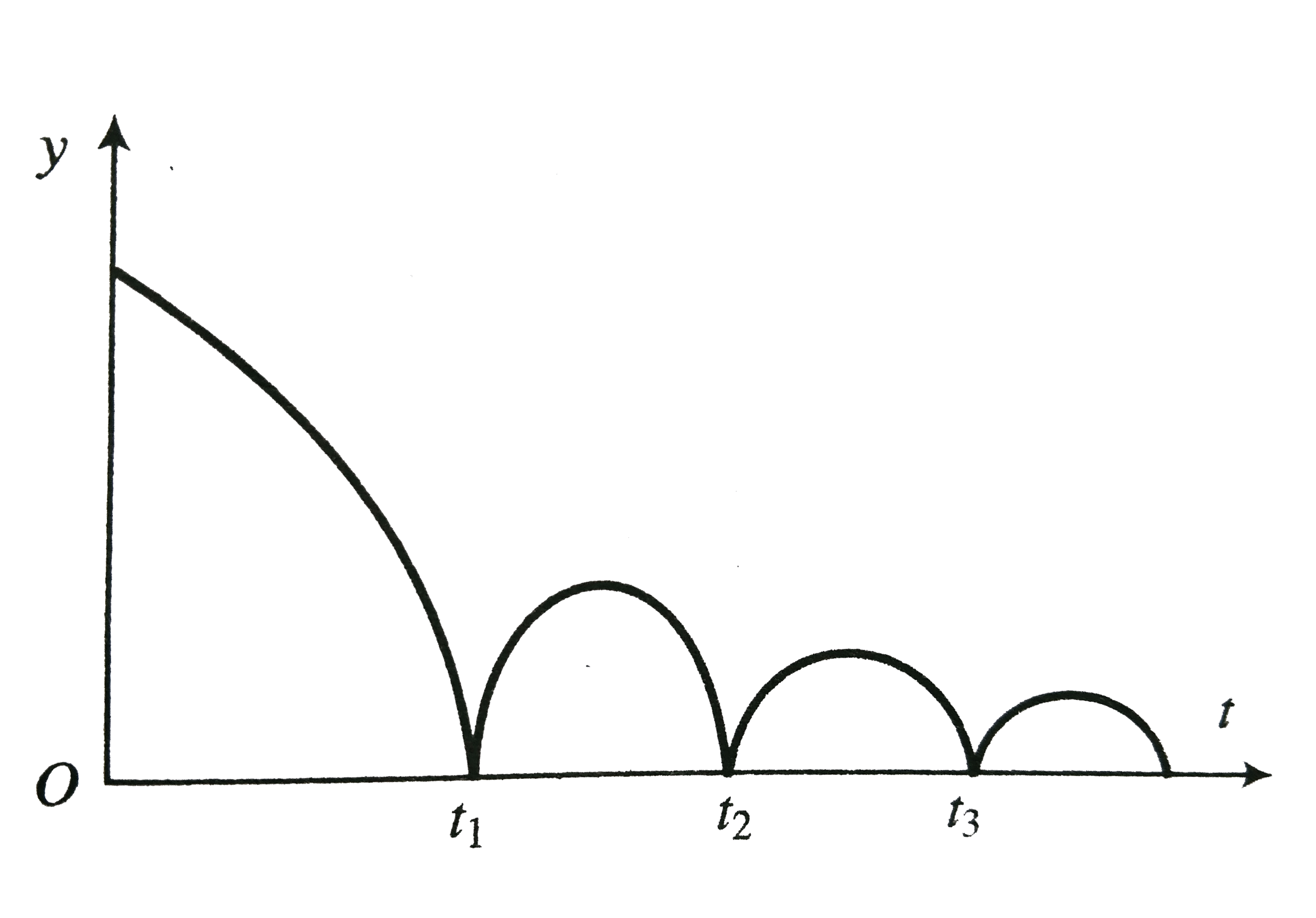 .
.
View SolutionA fielder in a cricket match throws ball from the boundary line to thhe wicket keeper. The ball describes a partabolic path. Which of the following quantities remain constant during the motion in air? (Neglecting air resistance)
View SolutionA fielder in a cricket match throws ball from the boudnary line to the wicket keeper. The ball describes at parabolic path. Which of the following quantities remain constant during the motion in air? (Neglecting air resistance)
View SolutionA ball falls vertically downward and bounces off a horizontal floor. The speed of the ball just before reaching the floor (u1) is equal to the speed just after having contact with the floor (u2) , u1=u2 . The corresponding magnitudes of accelerations are denoted respectively by a1 and a2 . The air resistance during motion is proportional to speed and is not negligible. If g is acceleration due to gravity, then–
View Solution