A solid cylinder of mass M and of radius R is fixed on a frictionless axle over a well. A rope negligible mass is wrapped around the cylinder. A bucket of uniform mass m is suspended from it. The linear acceleration bucket will:
mgM+m
2mgM+m
2mgM+2m
2mg2M+m
The correct Answer is:C
Step by step video, text & image solution for A solid cylinder of mass M and of radius R is fixed on a frictionless axle over a well. A rope negligible mass is wrapped around the cylinder. A bucket of uniform mass m is suspended from it. The linear acceleration bucket will: by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
A uniform solid cylinder of mass M and of radius R rotates about a frictionless axle. Two masses are suspended from a rope wrapped arround the cylinder. If the system is released from rest, the tension in each rope is?
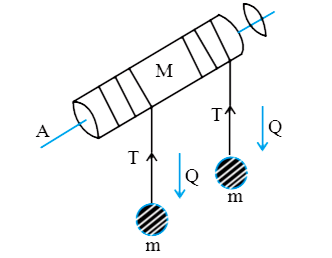 View Solution
View SolutionA solid cylinder of mass M and of radius R is fixed on a frictionless axle over a well. A rope negligible mass is wrapped around the cylinder. A bucket of uniform mass m is suspended from it. The linear acceleration bucket will:
View SolutionA uniform disc of mass M and radius R is mounted on an axle supported in frictionless bearings. A light cord is wrapped around the rim of the disc and a steady downward pull T is exerted on the cord. The angular acceleration of the disc is
View SolutionA solid cylinder of mass m and radius r is rolling on a rough inclined plane of inclination θ. The coefficient of friction between the cylinder and incline is μ. Then.
View SolutionA cylinder of mass m and radius R rolls down an inclined plane of inclination θ. Calculate the linear acceleration of the axis of cylinder.
View SolutionA cylinder of mass m and radius R rolls down an inclined plane of inclination θ. Calculate the linear acceleration of the axis of cylinder.
View Solution
A uniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force F is applied at the top point P of the cylinder so that it start pure rolling. The acceleration of the cylinder isView SolutionA solid cylinder of mass M and radius R rolls down an inclined plane of height h. The angular velocity of the cylinder when it reaches the bottom of the plane will be :
View SolutionA solid cylinder of mass M and radius R has a light thin tape wound around it as shown in the figure. The tape passes over a light, smooth fixed pulley to a block of mass m. Find the linear acceleration of the cylinder's axis up the incline (in) assuming no slipping. Given mass of the block = 1.5Kg, mass of the cylinder = 2 kg, the angle inclination = 30° and take g=10ms−2
View SolutionA solid cylinder of mass M and radius R pure rolls on a rough surface as shown in the figure. Choose the correct alternative (s).
 View Solution
View Solution


