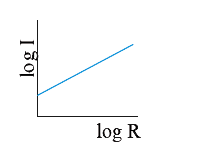
In the above question, the curve between log I and log R will be :



The correct Answer is:B
To solve the problem, we need to analyze the relationship between the moment of inertia I of a solid cylinder and its radius R. The moment of inertia about the axis through the center of mass for a solid cylinder is given by the formula:
I=12mR2
Where:
- I is the moment of inertia,
- m is the mass of the cylinder,
- R is the radius of the cylinder.
Step 1: Express the Moment of Inertia in Terms of Logarithms
We can take the logarithm of both sides of the equation to analyze the relationship between logI and logR:
logI=log(12mR2)
Using the properties of logarithms, we can separate the terms:
logI=log(12)+logm+logR2
Further simplifying, we have:
logI=log(12)+logm+2logR
Step 2: Rearranging the Equation
We can rearrange the equation to express it in the form of a linear equation y=mx+c:
logI=2logR+(logm+log(12))
Here, we can identify:
- y=logI
- x=logR
- The slope m=2
- The y-intercept c=logm+log(12)
Step 3: Analyzing the Graph
From the equation logI=2logR+c, we can see that if we plot logI on the y-axis and logR on the x-axis, the graph will be a straight line with:
- A slope of 2,
- A y-intercept of c.
Conclusion
The curve between logI and logR will be a straight line with a slope of 2. This indicates that as the radius R increases, the moment of inertia I increases quadratically.
- I is the moment of inertia,
- m is the mass of the cylinder,
- R is the radius of the cylinder.
We can take the logarithm of both sides of the equation to analyze the relationship between logI and logR:
We can rearrange the equation to express it in the form of a linear equation y=mx+c:
- y=logI
- x=logR
- The slope m=2
- The y-intercept c=logm+log(12)
From the equation logI=2logR+c, we can see that if we plot logI on the y-axis and logR on the x-axis, the graph will be a straight line with:
- A slope of 2,
- A y-intercept of c.
The curve between logI and logR will be a straight line with a slope of 2. This indicates that as the radius R increases, the moment of inertia I increases quadratically.
Similar Questions
Knowledge Check
When a current I is passed through a wire of constant resistance, it produces a potential difference V across its ends. The graph drawn between log I and log V will be
A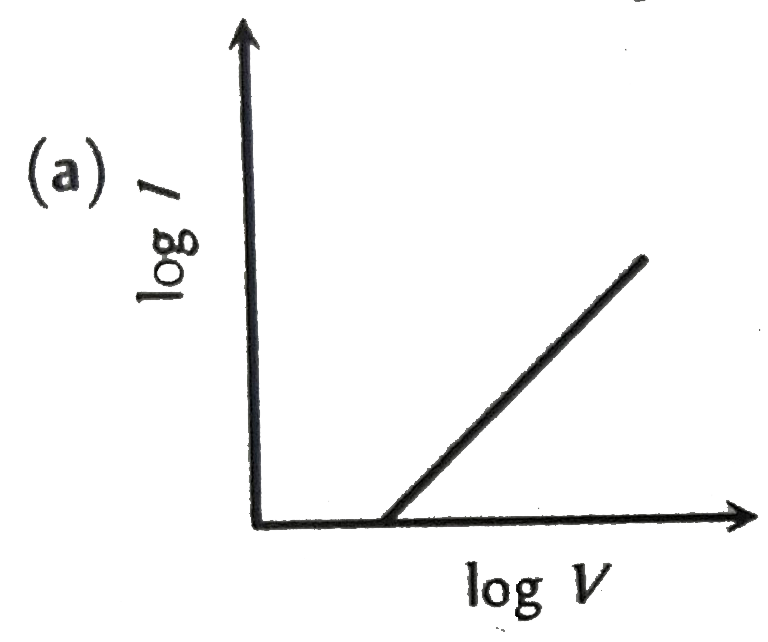 B
B C
C D
D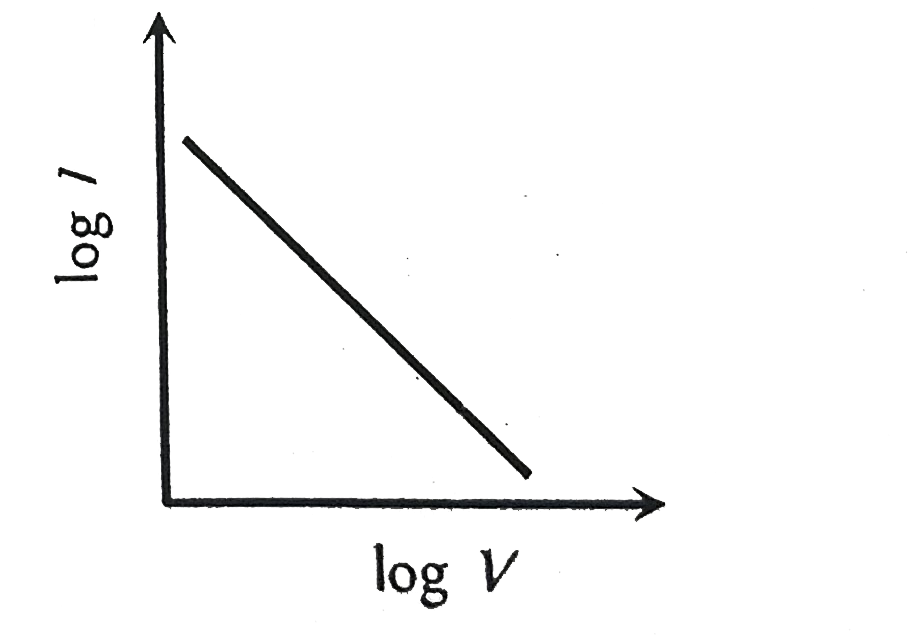
The current curve between logejT2 and lT
A B
B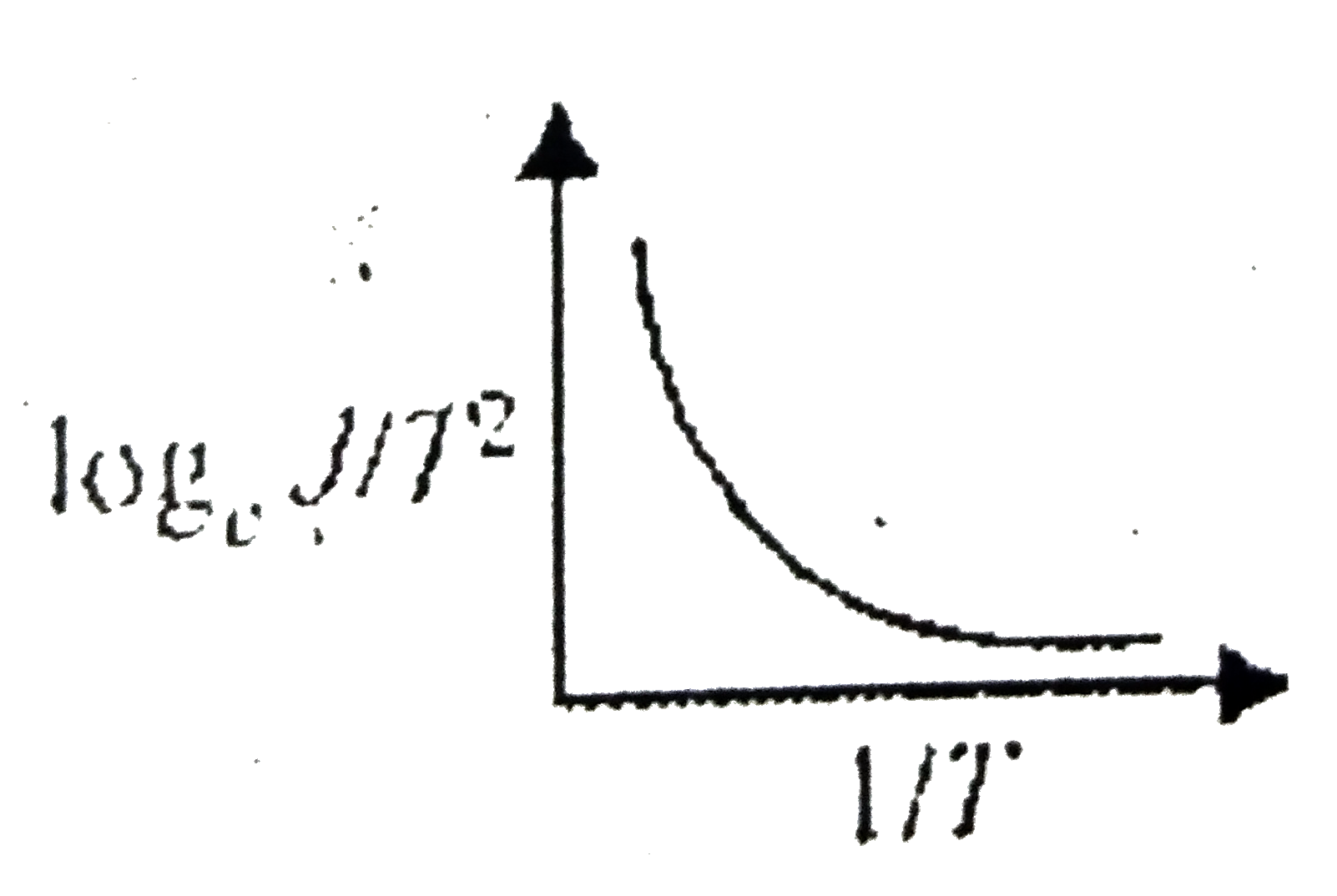 C
C D
D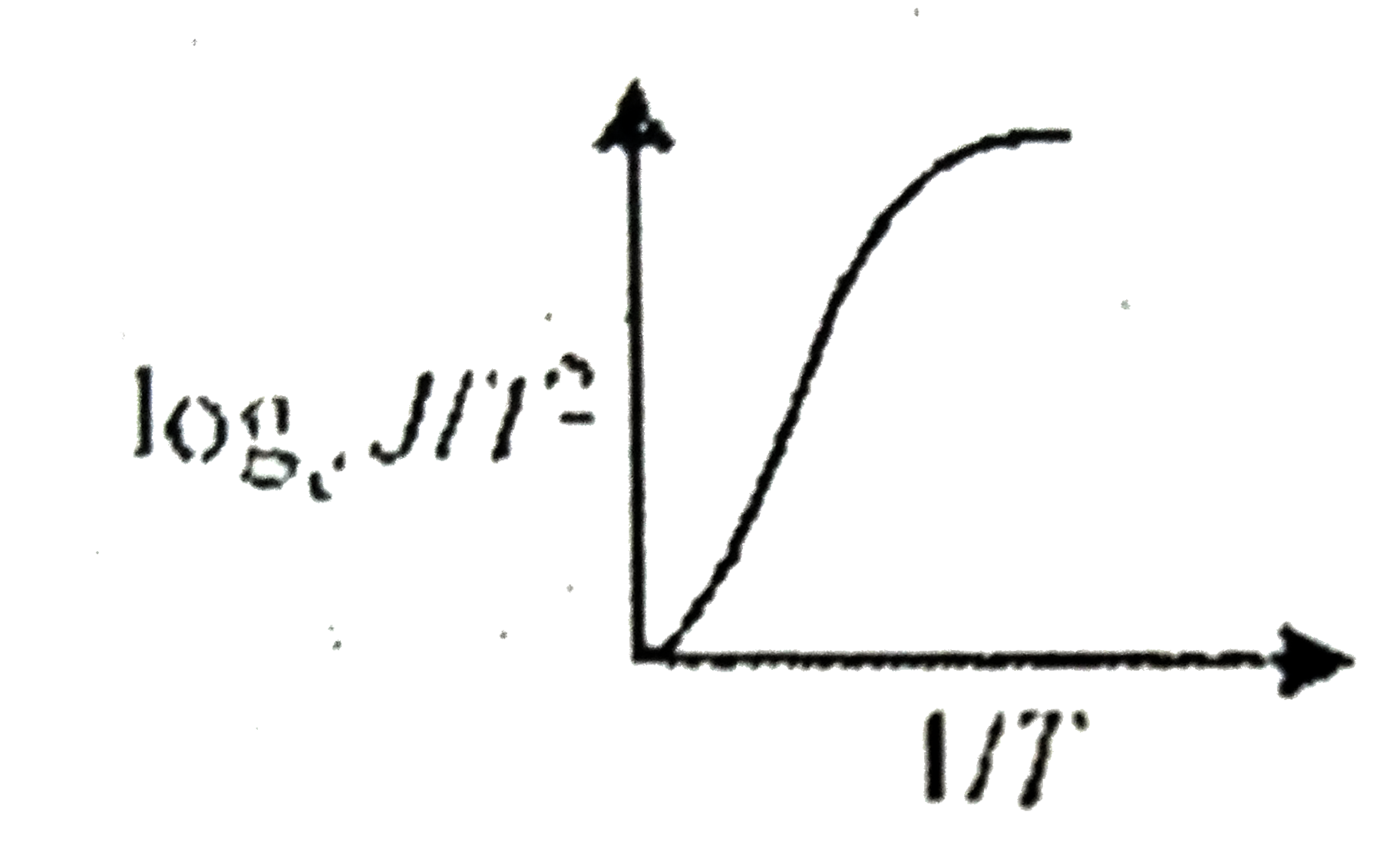
The correct curve between logeR and loge(θ−θo) is -
A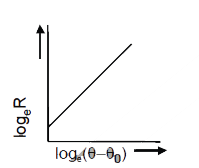 B
B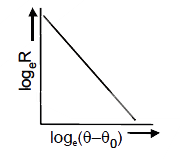 C
C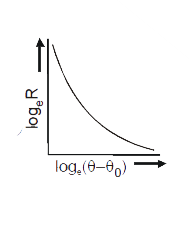 D
D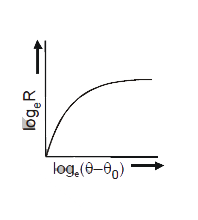
The area of the region bounded by the curves y=exlogxandy=logxex is
View SolutionThe area between the curves y=lnxandy=(lnx)2 is
View SolutionWhich of the following curves between log K and 1T is correct?
View SolutionIf a,b,c are the pth,qthandrth terms of G.P then the angle between the vector →u=(loga)ˆi+(logb)ˆj+(logc)ˆkand→v−(q−r)ˆi+(r−p)ˆi+(r−p)ˆj+(p−q)ˆk, is
View SolutionWhich of these examples will have the steepest curve when log of species richness and log of area are plotted on a graph?
View Solution

